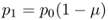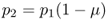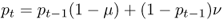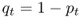4.1 The Nature of Mutations

Mutations are random changes in genetic code. Returning to the idea that genetic transmission is the transmission of information, from cell to cell and from generation to generation, a mutation is an error in the transmission. Any transmission of information is subject to errors, whether this is static on a phone line or a smudged fax transmission. I recall from grade school a game we played one day that involved the transmission of information. The teacher started the game by whispering a message to the first student in the first row of the classroom. This student then whispered the message to the student immediately behind in the second row, who in turn whispered the message to the next student in line. This whispering sequence continued up and down the rows of the class until the last student gave the message to the teacher, who then wrote both the original and last messages on the board. I cannot recall what the message was, but I do remember that it had changed somewhat because of accumulated errors in transmission from one student to the next. As a broad analogy, this was an example of a mutation. In genetics, the same thing can happen when information is not replicated exactly from one cell to the next. In our body cells, this can cause damage, including cancer. If such a mutation occurs in a sex cell, then this information becomes evolutionarily significant because it changes the transmission of genetic information from one generation to the next.

4.1.1 Types of Mutation

Mutations are random changes in the genetic code that occur for a number of reasons, including chemical exposure, ultraviolet radiation, viral infection, and background radiation. Mutations can occur in a variety of ways, some of which are reviewed here briefly.

4.1.1.1 Point Mutations

The simplest form of mutation is a point mutation, where there is a change from one DNA base to another, such as from C to T, or from A to C. The four nucleotide bases have different biochemical structures. Bases A and G are purines, which are defined as having two carbon–nitrogen rings. Bases C and T are pyrimidines, which are defined as possessing one carbon–nitrogen ring. When the mutation is between two purines (A and G) or between two pyrimidines (C and T), it is called a transition. When the mutation is between a purine and a pyrimidine (A and C, A and T, G and C, or G and T), it is called a transversion. Transitions are much more common than transversions.

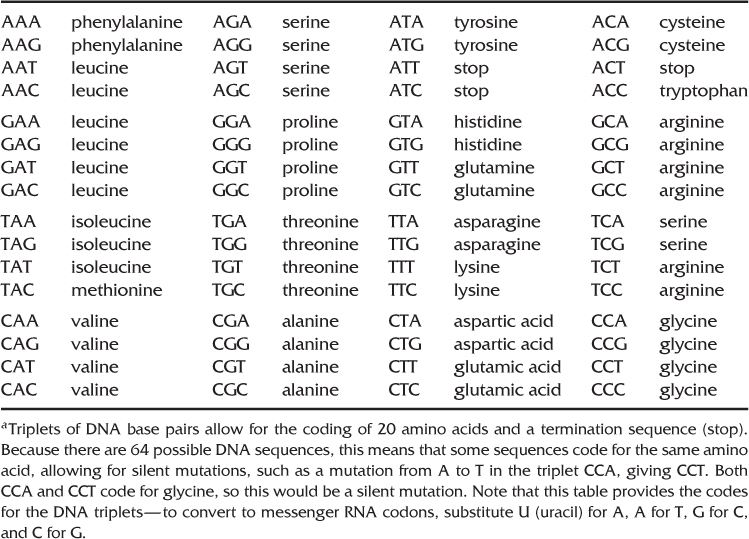
Point mutations can have differing effects. If a point mutation occurs in a noncoding part of the DNA, with no impact on the organism, then this mutation can be considered neutral. For coding DNA, some point mutations can be neutral if the mutation results in the same amino acid, which is known as a silent mutation (see Table 4.1). An example is the genetic code for the amino acid glycine. There are four different DNA sequences that code for glycine: CCA, CCT, CCC, and CCG. If there is a DNA sequence of CCA and the last base pair changes from A to G, giving the sequence CCG, the code is still for the same amino acid. Note that we would be able to detect this mutation from a direct assessment of the DNA sequence but not from analysis of amino acids—the change would be “silent” at this level. For other point mutations, there can be a more noticeable impact. For example, a point mutation for the sixth amino acid in the beta chain of the hemoglobin molecule results in a change from the amino acid glutamic acid to the amino acid valine, which results in a variant form of hemoglobin known as sickle cell hemoglobin. Individuals with two copies of this allele have the genetic disease known as sickle cell anemia (see Chapter 7 for more information on the evolution of the sickle cell allele).

Table 4.1 DNA Triplets for Coding of Amino Acidsa

4.1.1.2 Insertions and Deletions

In addition to changes due to substitution in the DNA, mutations can also produce insertions and deletions of DNA sequences. The term indel is used to refer to insertions and deletions collectively. A change in DNA sequence through the insertion or deletion of base pairs can change the function of a gene. An example is found in the CCR5 gene in humans, found on chromosome 21, which codes for a receptor protein. One mutant allele is known as the CCR5-Δ32 allele (Δ is the Greek letter delta, often used to denote difference). This mutation consists of a 32-bp deletion in the gene, which changes the biochemical properties of the CCR5 protein. One interesting consequence of this allele is that people who inherit two copies (having the CCR5-Δ32–CCR5-Δ32 genotype) are resistant to infection from HIV, the virus that causes AIDS (more information on this mutation is given in Chapter 7).

4.1.1.3 Chromosomal Changes

Mutations can also affect large sections of entire chromosomes. Such changes include inversions, where a section of a chromosome winds up in reverse order. Mutation can also cause deletion of large chunks of a chromosome. Translocations occur when sections of a chromosome move to another chromosome; some of these involve an exchange of DNA between chromosomes, and some do not. Entire chromosomes can also be replicated. Down syndrome, for example, is caused when there is an extra twenty-first chromosome.

4.1.2 The Evolutionary Impact of Mutation

Three major points need to be kept in mind regarding mutation and evolution. First, mutation is the ultimate source of all genetic variations. Whether this is diversity in blood types, single nucleotide polymorphisms (SNPs), or other genetic traits, different alleles start out as mutations. The second major point, as noted earlier, is that a mutation will have a direct evolutionary consequence only if it occurs in a sex cell, because that is the only way that a mutation can be passed on to the next generation. The third point to keep in mind is that mutation is random with respect to its evolutionary significance. In other words mutations do not appear because they would be useful for a population to possess at a given point in time.

Mutation is an evolutionary force because it leads to a change in allele frequency over time. To illustrate this, imagine a locus with a single allele A in a population of 2000 people. Because all 2000 people have two copies of the A allele (genotype AA), there are 4000 A alleles in the population. Now, imagine that a mutation occurs in one of the A alleles, leading to a new allele designated as a. We now have 3999 A alleles and one a allele. The frequency of the A allele has changed from 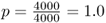to . 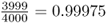The frequency of the a allele has changed from 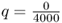to 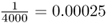. Admittedly, this is a very small change, but it is still a change. Remember that one of the assumptions of Hardy–Weinberg equilibrium is that there are no mutations. When mutations do occur, the allele frequencies change from those expected under Hardy–Weinberg equilibrium.

The major evolutionary significance of mutation is to introduce new alleles into a population. By itself, mutation does not lead to major shifts in allele frequency. As such, mutation is a necessary, but not sufficient, cause of evolution. Mutation is the ultimate source of all genetic variation, and evolution would not be possible without it. On the other hand, evolution is not simply the accumulation of mutations. By itself, mutation can only introduce new genetic variants into a population, but cannot lead to major changes in allele frequencies over reasonable lengths of evolutionary time. The other evolutionary forces (selection, drift, gene flow) act on new mutants as they arise in a population, causing them to sometimes decrease, and sometimes increase, in frequency. Thus, discussion of some of the population genetics of mutation is actually deferred until later in this book when interactions of mutation with other evolutionary forces are considered.

4.1.3 Rates of Mutation

Mutations can be regarded as relatively rare events when we consider the probability of a mutation occurring in an individual at a given locus in a given generation. Although generally low at this level, the exact rate of mutation varies across different parts of the genome and among species. Rates also vary depending on whether we are talking about a specific base pair, an entire locus, or the entire genome. For example, in humans the average mutation rate for a single site is about 2.3 × 10−8 (0.000000023) per base pair per generation. Of these, transitions tend to occur more frequently than transversions, and some transitions have even higher rates (“hotspots” of mutation) (Jobling et al. 2004). Indel mutations have lower mutation rates, averaging about 2.3 × 10−9. Repeated units of DNA, such as short tandem repeats and minisatellites, have higher mutation rates (Rosenberg et al. 2003b; Jobling et al. 2004). Mitochondrial DNA has higher mutation rates than does nuclear DNA (Stoneking 1993). Regardless of this variation, the main point to remember is that even for rapidly mutating sections of our genome, mutation alone cannot lead to major changes in allele frequency, even over long periods of time.

4.2 Models of Mutation

4.1

If, for example, we start with p0 = 1.0 with a mutation rate of μ = 1 × 10−6 = 0.000001, then p1 = 0.999999.

We can now go further and consider what will happen in generation 2 after an additional generation of mutation. Following the same logic as used to derive equation (4.1), we can express the expected frequency of the A allele in generation 2 as a function of the expected frequency of the A allele in generation 1 and the mutation rate

4.2

which would give p2 = 0.999998. We could continue performing this calculation generation after generation, but this gets rather tiring. Instead, we can take a shortcut by noting what happens when we substitute equation (4.1) into equation (4.2):

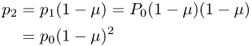
If we do this for another generation (t = 3), we get

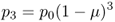
We can easily see now that these results can be extended to any number of generations, and all we need to know is the initial value of p (p0), the mutation rate (μ), and the number of generations (t):

4.3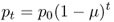

Because we have only two alleles, and because p + q = 1, the frequency of the a allele in generation t is therefore

4.4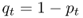

For example, if we start with allele frequencies of p0 = 1 and q0 = 0 and a mutation rate of μ = 1 × 10−6, then, after 10,000 generations, we will have p10, 000 = 0.99005 and q10, 000 = 0.00995.

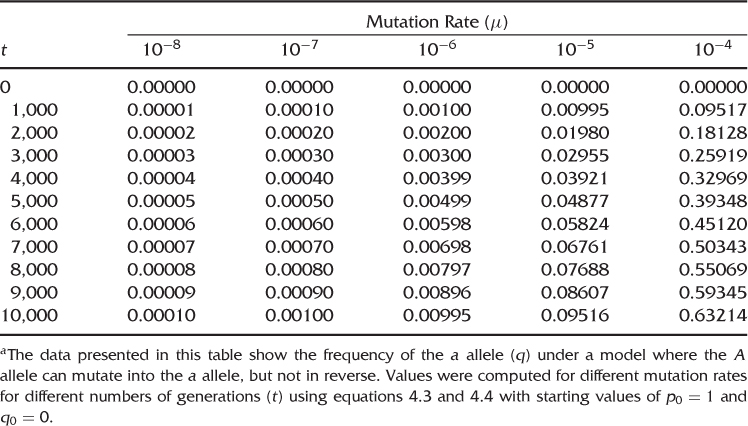
The higher the mutation rate, the more change will result. Table 4.2 shows frequencies of a mutant allele for different mutation rates at different numbers of generations. For low mutation rates characteristic of most point mutations, there is very little change even after 10,000 generations. For higher mutation rates, there is a greater amount of change, but it is still relatively low for most rates. Only when the mutation rate is very high (10−4) do we see more change, and even then, the accumulation of mutation takes several thousand generations. Eventually, the mutant allele would replace the other allele, but this would take a very long time, even with high mutation rates. These slow rates of change due to mutation are analogous to the slow pace with which a dripping tap will fill a bathtub.

Table 4.2 Allele Frequencies under Irreversible Mutationa

4.2.2 Reverse Mutation

Before looking at the evolutionary implications of the slow pace of the irreversible mutation model, we should examine what happens when we relax the assumption that mutations are irreversible. Under a model of reverse mutation, we will allow mutation back from the a allele to the A allele as well as the mutation of A to a. As before, we use the symbol μ to represent the probability that an A allele will mutate into an a allele. We will also use the symbol ν, the Greek letter nu, to represent the probability that an a allele will mutate back into an A allele. Let us start with p0 as the initial frequency of the A allele. What will this frequency be after a generation under the model of reversible mutation?

Under the model of reverse mutation there are two ways to obtain an A allele in the next generation. First, a certain proportion of A alleles will not mutate. As shown earlier, the probability of an A allele not mutating into an a allele is, from equation (4.1), equal to p1 = p0(1 − μ). Because mutation is reversible, we can also get an A allele that has mutated back from an a allele. The probability of this happening is the product of the probability of having an a allele ( = q = 1 − p) and the probability of an a allele mutating ( = ν), giving the probability (1 − p)ν. We now have two different ways of obtaining an A allele, so we use the or rule to figure out the probability of an A allele not mutating or an a allele mutating into A. We add these probabilities, giving

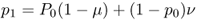
We could then calculate the allele frequency in the next generation (p2) using the same logic. In general, we can express the allele frequencies in any given generation (t) in terms of the mutation rates and the allele frequencies in the previous generation (t − 1) as

4.5

and the frequency of the a allele as

4.6

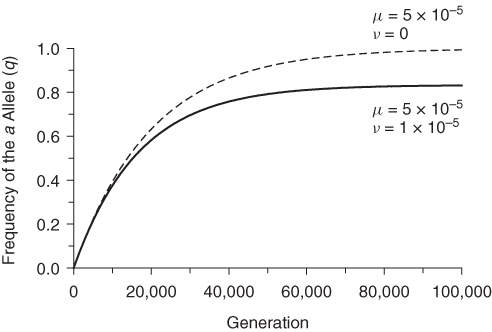
The impact of reverse mutation is shown in Figure 4.1, which tracks the frequency of the a allele over 100,000 generations starting with an initial frequency of q0 = 0, a mutation rate of μ = 5 × 10−5, and a reverse mutation rate of ν = 1 × 10−5. This case is contrasted with the case where there is no reversible mutation (ν = 0). In both cases, the frequency of the mutant allele increases slowly over time (the dripping tap analogy). Under reversible mutation, the increase slows down over time and levels off to a value a bit higher than q = 0.8. This happens because an equilibrium is approached between the addition of new a alleles (mutating from A) and the subtraction of preexisting a alleles that mutate back into A. In terms of the dripping tap analogy, consider a leaky faucet that is slowly filling a bathtub, but there is an outlet drain about 80% of the height of the tub. The water continues to enter the bathtub but does not overflow because the incoming water is balanced by the loss of water through the drain.

Figure 4.1 The frequency of a mutant allele under reversible mutation. The solid line shows changes in the frequency of the a allele (q) starting with an initial value of q0 = 0 with a mutation rate (A → a) of μ = 5 × 10−5, and a reverse mutation rate (a → A) of ν = 1 × 10−5. Values were computed using equations (4.5) and (4.6). Reverse mutation is contrasted with the case of irreversible mutation (dashed line) with μ = 5 × 10−5 and ν = 0. Under reversible mutation, the frequency of q approaches an equilibrium between new mutations and reverse mutations, which is defined as μ/(μ + ν) = (5 × 10−5)/(5 × 10−5 + 1 × 10−5) = 0.8333 [see equation (4.10) in text].

Stay updated, free articles. Join our Telegram channel

Join