and Miguel A. R. B. Castanho2
(1)
Instituto de Bioquímica Médica Leopoldo de Meis, Federal University of Rio de Janeiro, Rio de Janeiro, Rio de Janeiro, Brazil
(2)
Institute of Biochemistry and Institute of Molecular Medicine, School of Medicine, University of Lisbon, Lisbon, Portugal
Cells are made up of molecules, but cells are not simple mixtures or assemblies of molecules. If thrown to a test tube separately or in a random mixture, the whole set of molecules of a cell would interact physically and react chemically, but would not spontaneously form a cell. Cells form and exist because the molecular events that create and maintain cells are highly ordered. The sequence and specific place of events and the flows of matter and energy are such that the cell is able to preserve stability and evolve by adaptation to a certain extent, as addressed in Sect. 1.1. In Part II, we will focus on some of the most important chemical reactions occurring in different tissues of the human body and their coordination so that one understands how the changes of matter and transfer of energy enable the human body to exist, move, adapt to external challenges, and reproduce. This ensemble of chemical reactions is called metabolism .
Because the whole metabolism is such a complex array of chemical reactions, biochemists tend to study and concentrate on subsets of reactions separately. The easiest form to understand and explain metabolism is to divide it in parts depending on the chemical nature of the molecules involved, i.e., according to the families of molecules addressed in Part I. So, for practical reasons and for the sake of simplicity, the whole metabolism, which is a single highly complex network of chemical reactions and physical events, is regarded as a sum of “metabolisms ”: the metabolism of saccharides , the metabolism of amino acid s , the metabolism of lipids , etc.
The part of metabolism more directly related to nutrient absorption and ATP production is the “energy metabolism.” The human body continuously transforms molecules, sometimes forming higher molar mass products, others breaking down molecules into smaller molar mass entities. Typically, these situations correspond to incorporate mass and energy from nutrients, or consuming such mass and energy in the absence of nutrient intake, respectively. The “metabolisms ” of the first kind are known as anabolic (construction), the latter being known as catabolic (degrading). So, “amino acid catabolism,” for instance, refers to the breakdown of amino acids into smaller molecules, as opposed to amino acid synthesis (amino acids anabolism). Amino acids, in turn, may polymerize and form proteins : protein anabolism, in contrast to the breakdown of proteins, amino acids resulting therefrom (protein catabolism). Subsets of reactions that are active in both catabolic and anabolic conditions are “amphibolic” (the prefix “amphi” referring to its dual nature). This is the case of the tricarboxylic acid (TCA) cycle, also known as Krebs cycle (see Sect. 7.2).
An example of generic metabolism is schematized in Fig. 4.1. No matter how complex the metabolism may seem at first glance, the interpretation of a scheme of consecutive reactions is simple and depends on the identification of five key factors:
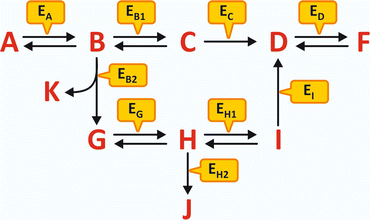

Fig. 4.1
Hypothetical schematic metabolism involving metabolites A to K and enzymes Ex (subscript X in Ex represents the substrate, X = A to K). The metabolism is “fed” by A and has K, F, and J as “end products.” An external source of G may also lead to the formation of J and F, but not K. An external source of D can only lead to the formation of F. However, if ED is not present or not operative, F will not be formed in any circumstance. Likewise, if EB2 is not present or not operative, K, G, H, J, and I will not be formed even in the presence of high concentration of B. If EB1 and EB2 are never active or inactive at the same time, F is always formed but not J; the reactions’ scheme assures the permanent formation of F but the selective formation of J when the control of the reaction course is performed by alternate states of activity of EB1 and EB2
1.
The reactants that originate the process
2.
The end products, regardless of being formed in intermediate reactions or the final reaction
3.
The branching points, i.e., steps where the sequence of reactions may follow different courses
4.
The irreversible reactions
5.
The specific reactions that are catalyzed by enzymes that are finely regulated and so have the ability to highly accelerate segments of the metabolism , or not
These five key factors in the interpretation of a metabolism will help the reader not to look to a metabolism as a chaotic ensemble of chemicals, enzymes , and reaction arrows. Metabolism is an appealing and richly informative text on the organization of life, should we be able to interpret it.
Enzymes are key protagonists of metabolisms together with metabolites (i.e., the intermediate reactants/products of the reactions of metabolisms). Not only enzymes greatly accelerate reactions, they are the entities that make metabolisms happen in specific directions. Their importance and action is better illustrated if one considers first a hypothetical metabolism without enzymes (described in Sect. 4.1) and the same set of reactions with enzymes (described in Sect. 4.2).
4.1 Consecutive Reactions Without Enzymes
Consider the simple chemical reaction:
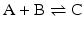 which in terms of a more amenable representation to biochemists may be written as:
which in terms of a more amenable representation to biochemists may be written as:
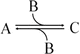
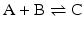
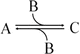
to highlight the conversion of A into C with the intervention of B. Nevertheless, one should not underestimate the importance of B in the balance of energy and mass of the reaction, even if B is H2O or a small ion, for instance, and A and C are big complex molecules. A, B, and C are all equally important to study the course and velocity of the reaction, i.e., the thermodynamics of the reaction. To better understand the basic principles that govern the chemical reaction, we will start with very simplistic formulations. One will assume that A and B are mixed at a specific instant in time (t = 0) and the reaction initiates forming C. As soon as C is formed, it will also start converting to A + B, but in the beginning only few molecules of C exist, so the velocity of the conversion of A + B into C is larger than the opposite conversion, C to A + B. Naturally, in this condition, the concentration of C will increase until the point in which the velocities of both reactions will match: the velocity with which C is formed equals the velocity with which it is consumed. The reaction takes place because A and B are continuously transformed into C and vice versa, but the concentrations of A, B, and C present in solution do not change. This is the point of equilibrium. At this stage it is important to dissociate the extent of the reaction (i.e., the fraction of A and B that was transformed to reach the equilibrium) and the velocity of the reaction, which is related to the time needed to reach the equilibrium. A very extensive reaction is represented by:
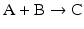 and named “irreversible” (therefore written with a one-way arrow), but this tells us absolutely nothing about the velocity of the reaction. In fact, the conversion of A and B into C may be so slow that in practical terms C is not formed. So, to study chemical reactions, one needs to address both the extent and the velocity of reactions. A favorable reaction has a high degree of conversion of reactants in products; a fast reaction reaches the equilibrium in a short time. Both aspects are independent of each other, and so it is not surprising that they can be modulated by separate means in metabolism .
and named “irreversible” (therefore written with a one-way arrow), but this tells us absolutely nothing about the velocity of the reaction. In fact, the conversion of A and B into C may be so slow that in practical terms C is not formed. So, to study chemical reactions, one needs to address both the extent and the velocity of reactions. A favorable reaction has a high degree of conversion of reactants in products; a fast reaction reaches the equilibrium in a short time. Both aspects are independent of each other, and so it is not surprising that they can be modulated by separate means in metabolism .
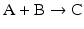
The extent of a reaction is described by the equilibrium constant, which in practical terms is calculated from the concentrations at equilibrium:
![$$ {K}_{eq}=\frac{{\left[\mathrm{C}\right]}_{eq}}{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equc.gif) It is obvious that unfavorable reactions have low K eq and favorable reactions have high K eq. K eq varies from nil to infinity. The determinants that contribute to the value of K eq for a given reaction (i.e., how favorable it is) relate to the balance of both released energy and order of the whole environment in which the reaction takes place. Neither is intuitive, but both can be experimentally demonstrated. Chemical reactions tend to consume more reactants as the products are more stable (“less energetic”) than reactants and the environment becomes more disordered with the presence of the products (i.e., closer to a random organization). The degree of disorder is generically referred to as entropy. The balance of energy and entropy are so deeply rooted in thermodynamics that they are the subject of the first and second laws of thermodynamics, respectively, as the founding principles of this discipline. The exact quantitative weighting between the balance of released energy as heat (the enthalpy, ΔH) and balance of entropy (ΔS) is provided by the parameter ΔG, the difference of the Gibbs energy during the chemical reaction:
It is obvious that unfavorable reactions have low K eq and favorable reactions have high K eq. K eq varies from nil to infinity. The determinants that contribute to the value of K eq for a given reaction (i.e., how favorable it is) relate to the balance of both released energy and order of the whole environment in which the reaction takes place. Neither is intuitive, but both can be experimentally demonstrated. Chemical reactions tend to consume more reactants as the products are more stable (“less energetic”) than reactants and the environment becomes more disordered with the presence of the products (i.e., closer to a random organization). The degree of disorder is generically referred to as entropy. The balance of energy and entropy are so deeply rooted in thermodynamics that they are the subject of the first and second laws of thermodynamics, respectively, as the founding principles of this discipline. The exact quantitative weighting between the balance of released energy as heat (the enthalpy, ΔH) and balance of entropy (ΔS) is provided by the parameter ΔG, the difference of the Gibbs energy during the chemical reaction:
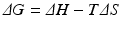 Assuming that the temperature, T, does not change in the process, ΔG is related to the concentration of reactants and products:
Assuming that the temperature, T, does not change in the process, ΔG is related to the concentration of reactants and products:
![$$ \varDelta G=\varDelta {G}^0+RT \ln \frac{\left[C\right]}{\left[A\right]\left[B\right]} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Eque.gif) In equilibrium ΔG = 0; therefore,
In equilibrium ΔG = 0; therefore,
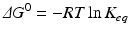 While thermodynamics may reach complex formulations to explain the interaction of energy with matter, we shall stick to those most important in medical biochemistry. Previous equations on ΔG are useful because they provide information about the spontaneity of reactions. If ΔG < 0 (exergonic reaction), the reaction will proceed spontaneously until equilibrium; if ΔG > 0 (endergonic reaction), the reaction will not be spontaneous; if ΔG = 0, the reaction is at equilibrium. Whether ΔG is positive, negative of nil depends largely on the concentrations of reactants and products, and the reaction will continue until these concentrations reach equilibrium (ΔG = 0). ΔG eq0 is related to the concentrations at equilibrium specifically and so provides information on the final extent of reaction (i.e., how far the reaction goes until equilibrium):
While thermodynamics may reach complex formulations to explain the interaction of energy with matter, we shall stick to those most important in medical biochemistry. Previous equations on ΔG are useful because they provide information about the spontaneity of reactions. If ΔG < 0 (exergonic reaction), the reaction will proceed spontaneously until equilibrium; if ΔG > 0 (endergonic reaction), the reaction will not be spontaneous; if ΔG = 0, the reaction is at equilibrium. Whether ΔG is positive, negative of nil depends largely on the concentrations of reactants and products, and the reaction will continue until these concentrations reach equilibrium (ΔG = 0). ΔG eq0 is related to the concentrations at equilibrium specifically and so provides information on the final extent of reaction (i.e., how far the reaction goes until equilibrium):
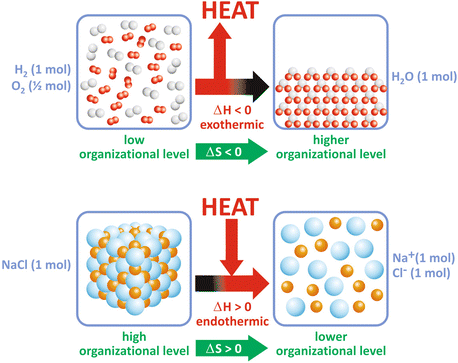
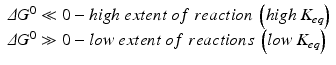 Box 4.1 illustrates these concepts for a simple reaction. Figure 4.2 shows two examples of how ΔH may dominate over ΔS and vice versa and be determinant for the extent of the reaction, i.e., for ΔG. However, in most biological processes related to the use of nutrients, ΔH is large compared to TΔS, which makes ΔH, the caloric “value” of food, an approximate measure of the total energy that can be used by the human body.
Box 4.1 illustrates these concepts for a simple reaction. Figure 4.2 shows two examples of how ΔH may dominate over ΔS and vice versa and be determinant for the extent of the reaction, i.e., for ΔG. However, in most biological processes related to the use of nutrients, ΔH is large compared to TΔS, which makes ΔH, the caloric “value” of food, an approximate measure of the total energy that can be used by the human body.
![$$ {K}_{eq}=\frac{{\left[\mathrm{C}\right]}_{eq}}{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equc.gif)
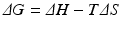
![$$ \varDelta G=\varDelta {G}^0+RT \ln \frac{\left[C\right]}{\left[A\right]\left[B\right]} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Eque.gif)
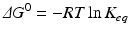
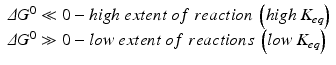

Fig. 4.2
Some reactions occur because the released energy, ΔH, compensates for the decrease in ΔS (a), or the increase in disorder compensates for the heat consumption (b)
Box 4.1: The Basic Thermodynamics of the Simplest Reaction
In the very simple case of one single reactant (R) being transformed in one single product (P):
 the equilibrium constant is:
the equilibrium constant is:
![$$ {K}_{eq}=\frac{{\left[P\right]}_{eq}}{{\left[R\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equi.gif) and
and
![$$ \varDelta {G}^0=-RT \ln {K}_{eq}=-RT \ln \frac{{\left[P\right]}_{eq}}{{\left[R\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equj.gif) It is obvious that:
It is obvious that:
![$$ \begin{array}{l}\varDelta {G}^o<0\kern0.46em if{\left[P\right]}_{eq}>{\left[R\right]}_{eq}\left({K}_{eq}>1\right)\hfill \\ {}\varDelta {G}^o>0\kern0.46em f{\left[P\right]}_{eq}<{\left[R\right]}_{eq}\left({K}_{eq}<1\right)\hfill \end{array} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equk.gif) The reactions with highest K eq have the most negative ΔG 0 eq. If the equilibrium is not yet attained, two situations are possible:
The reactions with highest K eq have the most negative ΔG 0 eq. If the equilibrium is not yet attained, two situations are possible:




![$$ {K}_{eq}=\frac{{\left[P\right]}_{eq}}{{\left[R\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equi.gif)
![$$ \varDelta {G}^0=-RT \ln {K}_{eq}=-RT \ln \frac{{\left[P\right]}_{eq}}{{\left[R\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equj.gif)
![$$ \begin{array}{l}\varDelta {G}^o<0\kern0.46em if{\left[P\right]}_{eq}>{\left[R\right]}_{eq}\left({K}_{eq}>1\right)\hfill \\ {}\varDelta {G}^o>0\kern0.46em f{\left[P\right]}_{eq}<{\left[R\right]}_{eq}\left({K}_{eq}<1\right)\hfill \end{array} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equk.gif)
1.
![$$ \begin{array}{l}\left[R\right]>{\left[R\right]}_{eq}\left(i.e.\left[P\right]<{\left[P\right]}_{eq}\right)\hfill \\ {}\varDelta G=\varDelta {G}^0+RT \ln \frac{\left[P\right]}{\left[R\right]}=+RT \ln \left(\frac{\left[P\right]}{\left[R\right]}\frac{{\left[R\right]}_{eq}}{{\left[P\right]}_{eq}}\right)\hfill \end{array} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equl.gif) which is obviously negative. The reactions will proceed with transformation of R in P until equilibrium, i.e., ΔG < 0 implies spontaneous transformation of reactants in products.
which is obviously negative. The reactions will proceed with transformation of R in P until equilibrium, i.e., ΔG < 0 implies spontaneous transformation of reactants in products.
![$$ \begin{array}{l}\left[R\right]>{\left[R\right]}_{eq}\left(i.e.\left[P\right]<{\left[P\right]}_{eq}\right)\hfill \\ {}\varDelta G=\varDelta {G}^0+RT \ln \frac{\left[P\right]}{\left[R\right]}=+RT \ln \left(\frac{\left[P\right]}{\left[R\right]}\frac{{\left[R\right]}_{eq}}{{\left[P\right]}_{eq}}\right)\hfill \end{array} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equl.gif)
2.
![$$ \left[R\right]<{\left[R\right]}:{eq}\left(i.e.\left[P\right]>{\left[P\right]}_{eq}\right) $$
” src=”/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equm.gif”></DIV></DIV></DIV></DIV><br />
<DIV id=Par19 class=]() This is the opposite case, in which ΔG > 0 and the spontaneous process is the reverse reaction, i.e., the transformation of the product P, in the reagent R.
This is the opposite case, in which ΔG > 0 and the spontaneous process is the reverse reaction, i.e., the transformation of the product P, in the reagent R.
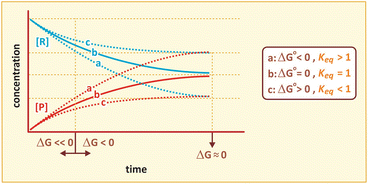
The relationship between ΔG, ΔG 0, and the course of reaction is represented in the figure below.

Isolated reactions such as the ones considered before are rarely relevant in metabolism as metabolism consists of consecutive reactions. So let us now consider the reaction
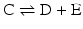 coupled to the first reaction,
coupled to the first reaction, 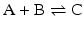 , to form:
, to form:
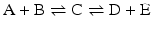 At equilibrium, it is obvious that the concentrations of A and B are related to the concentrations of D and E because C takes part in both reactions. In term of equilibrium constants:
At equilibrium, it is obvious that the concentrations of A and B are related to the concentrations of D and E because C takes part in both reactions. In term of equilibrium constants:
![$$ \begin{array}{l}{K}_{eq,1}=\frac{{\left[\mathrm{C}\right]}_{eq}}{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}}\hfill \\ {}{K}_{eq,2}=\frac{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}}{{\left[\mathrm{C}\right]}_{eq}}\hfill \end{array} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equp.gif) (1 and 2 refer to the first and second reactions in the sequence).
(1 and 2 refer to the first and second reactions in the sequence).
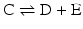
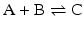 , to form:
, to form: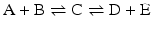
![$$ \begin{array}{l}{K}_{eq,1}=\frac{{\left[\mathrm{C}\right]}_{eq}}{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}}\hfill \\ {}{K}_{eq,2}=\frac{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}}{{\left[\mathrm{C}\right]}_{eq}}\hfill \end{array} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equp.gif)
Therefore,
![$$ {K}_{eq,1}{K}_{eq,2}=\frac{{\left[\mathrm{D}\right]}_{eq}{\left[\mathrm{E}\right]}_{eq}}{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equq.gif) which is the apparent equilibrium constant of the abbreviated form (“sum of reactions”) of the reactions
which is the apparent equilibrium constant of the abbreviated form (“sum of reactions”) of the reactions 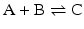 and
and 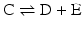 above:
above:
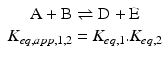 The amazing consequence is that ΔG° of the global process is simply the sum of ΔG of the two consecutive reactions:
The amazing consequence is that ΔG° of the global process is simply the sum of ΔG of the two consecutive reactions:
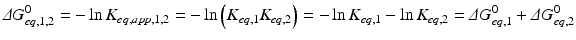 The consequences of metabolism are immense because it is implied that the conversion of C in D + E may be extremely unfavorable, but the extent to which A + B is converted to C “pushes” the reaction toward the formation of D + E through the increase in the concentration of C. This can be generalized to any set of consecutive reactions, and metabolisms are generally composed by favorable and unfavorable reactions influencing each other. In the extreme case where an irreversible reaction follows one or more reversible reactions, such as
The consequences of metabolism are immense because it is implied that the conversion of C in D + E may be extremely unfavorable, but the extent to which A + B is converted to C “pushes” the reaction toward the formation of D + E through the increase in the concentration of C. This can be generalized to any set of consecutive reactions, and metabolisms are generally composed by favorable and unfavorable reactions influencing each other. In the extreme case where an irreversible reaction follows one or more reversible reactions, such as
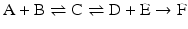 it is obvious that regardless of how unfavorable the first and second reactions may be, the end result is the total depletion of A and/or B and the formation of F. The same would happen in
it is obvious that regardless of how unfavorable the first and second reactions may be, the end result is the total depletion of A and/or B and the formation of F. The same would happen in
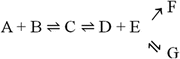
![$$ {K}_{eq,1}{K}_{eq,2}=\frac{{\left[\mathrm{D}\right]}_{eq}{\left[\mathrm{E}\right]}_{eq}}{{\left[\mathrm{A}\right]}_{eq}{\left[\mathrm{B}\right]}_{eq}} $$](/wp-content/uploads/2016/11/A215639_1_En_4_Chapter_Equq.gif)
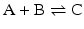 and
and 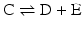 above:
above: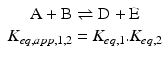
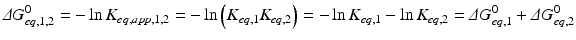
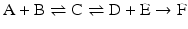
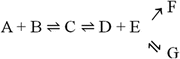
but not in
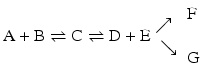 in which the end products would be both F and G. Although both the formation of F and G are irreversible, they are competing reactions. Although they both occur to the total depletion of at least one of the reagents, the product of the fastest reaction dominates. One of the reactions may be much faster than the other, in which case only one product forms in practice.
in which the end products would be both F and G. Although both the formation of F and G are irreversible, they are competing reactions. Although they both occur to the total depletion of at least one of the reagents, the product of the fastest reaction dominates. One of the reactions may be much faster than the other, in which case only one product forms in practice.
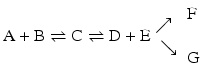
In a branched chain of reactions with an irreversible conversion such as, for instance,
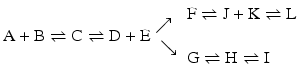 the final outcome critically depends on the irreversible steps and the branching points. Thus, the result may be complex.
the final outcome critically depends on the irreversible steps and the branching points. Thus, the result may be complex.
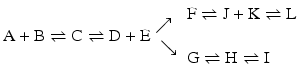
Given the importance of the velocity of reactions to the course of chain reactions, we shall now address kinetics in more detail as ΔG 0 only accounts for how far the reaction goes in the degree of conversion of reactants into products, not kinetics.
4.2 Consecutive Reactions With Enzymes
The chain of reactions above is dominated by the irreversibility of reactions 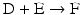 and
and 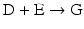 (
(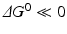 for both). If the latter, for instance, is much faster than the first, the metabolites G, H, and L will dominate. In the opposite case, F, J, K, and I will dominate.
for both). If the latter, for instance, is much faster than the first, the metabolites G, H, and L will dominate. In the opposite case, F, J, K, and I will dominate.
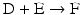 and
and 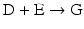 (
(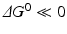 for both). If the latter, for instance, is much faster than the first, the metabolites G, H, and L will dominate. In the opposite case, F, J, K, and I will dominate.
for both). If the latter, for instance, is much faster than the first, the metabolites G, H, and L will dominate. In the opposite case, F, J, K, and I will dominate.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


