1.1 The Scope of Population Genetics
Before getting too far into the application of population genetics to the human species, it is useful to answer the basic question “What is population genetics?” This question can be answered by considering the nature of the broader field of genetics, the study of heredity in organisms. Genetics can be studied at various levels. The study of molecular genetics deals with the biochemical nature of heredity, specifically DNA and RNA. At this level, geneticists focus on the biochemical nature of heredity, including the structure and function of genes and other DNA sequences.
The study of Mendelian genetics, named after the Austrian monk, Gregor Mendel (1822–1884), is concerned with the process and pattern of genetic inheritance from parents to offspring. Mendel’s work gave us a basic understanding of how inheritance works, and how discrete units of inheritance combine to produce genotypes and phenotypes. Whereas the focus of molecular genetics is on the transmission of information from cell to cell, Mendelian genetics focuses on the transmission of genetic information from one individual (a parent) to another (the offspring). Mendelian genetics is in essence a statistical subject, dealing with the probability of different genotypes and phenotypes in offspring. A classic example concerns two parents, each of which carries one copy of a recessive gene. The principles of probability show that the chance of any given offspring having two copies of that gene, one from each parent, is 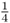 . These principles will be reviewed later, but for now, you should just consider that the transmission of genetic information is subject to the laws of probability.
. These principles will be reviewed later, but for now, you should just consider that the transmission of genetic information is subject to the laws of probability.
Population genetics takes this concern with the probability of transmitting genetic information from one generation to the next and extends it to the next level, an entire population (or set of populations, or even an entire species). In population genetics, we are concerned with the genetic composition of the entire population, and how this composition can change over time. For example, consider the classic example of the peppered moth in England. This species of moth comes in two forms, a dark-colored form and a light-colored form. Centuries ago, most moths were light-colored, and only about 1% were dark-colored. Dark-colored moths were rare because they would be more clearly visible against the light color of the tree trunks, making it easier for birds to see them and eat them. Over time, the environment changed, and the frequency of dark-colored moths increased as the frequency of the light-colored moths decreased. Because the color of the moths reflects genetic differences, this observed change is an example of the genetic composition of a species changing over time. Population genetics deals with explaining such changes. In this case, the initial origin of a different form is due to mutation, and the change in moth color over time reflects natural selection, because the environment had shifted following the Industrial Revolution, leading to darker tree trunks, thus creating a situation where dark-colored moths were less likely to be eaten by birds.
When the genetic makeup of a population changes over time, even in a single generation, we have a case of evolution. Population genetics is the branch of genetics that deals with evolutionary change in populations of organisms, and provides the mathematical basis of evolutionary theory. Note that I am using the word theory here in the context of the natural sciences, where a theory is a set of hypotheses that have been tested and have withstood the test of time, as compared with the popular use of the word theory as a simple hypothesis. When we speak of evolutionary theory, we are not stating that evolution may or may not exist, but instead are referring to a set of principles that explain the facts of evolution (in other words, beware of the statement that “evolution is a theory and not a fact,” because it is actually both a fact and a theory).
Evolution can be viewed over different scales of time and units of analysis. Population genetics deals with changes within a species over relatively short intervals of time, typically on the order of a small number of generations. This type of evolutionary change is also known as microevolution, and is contrasted with macroevolution, which focuses on the evolution of species and higher levels (genera, families, etc.), and typically deals with geological timescales, ranging from thousands to millions of years. Although macroevolution and microevolution are related in a theoretical sense, there is continued debate over the extent to which long-term macroevolutionary events are a straightforward extrapolation of microevolutionary trends (Simons 2002). The focus of this book is primarily on the theory of microevolution.
Population genetics is concerned with changes in genetic variation over time, that is, genetic differences and similarities. There are two ways of looking at genetic variation: variation within populations and variation between populations. The former refers to differences and similarities of individuals within a population; the latter refers to average differences between two or more populations. Later chapters will introduce quantitative measures of within-group and between-group variation based on genetic traits, but for the moment, I will use a simple analogy looking at adult human height. Picture yourself in a large classroom filled with students, and imagine that we measured everyone’s height. We would use these measurements to compute how much variation existed within the classroom. If, for example, everyone in the class were of exactly the same height, there would be no variation. If, however, there were differences in height, with everyone being between 5 ft 8 in tall and 5 ft 10 in. tall, then variation would exist because not everyone would be the same. If everyone were between 5 and 6 ft tall, there would be even more variation.
On the other hand, suppose that we want to compare the height in your classroom with the height in the next classroom. An example would be if the average height in your classroom were 5 ft 9 in. and the average height in the other classroom were 5 ft 8 in. The difference in average height would be 1 in. This difference would be an example of variation between groups. If the average height of the two classes were the same, then there would be no variation between groups. In evolutionary terms, we are interested in changes in genetic variation that take place both within and between populations.
By studying genetic change over time and its effects on genetic variation within and between populations, we are able to apply the theory of population genetics to address a wide variety of questions about human variation and evolution. A small sample of such questions (which will be addressed in later chapters) includes
- How much inbreeding occurs in human populations, and what is the effect of this inbreeding?
- What does genetic variation tell us about our species’ history?
- Can genetics to be used to trace ancient human migrations?
- Where did the first Americans come from?
- Why do some human populations have high frequencies of the harmful sickle cell allele?
- Are certain genes resistant to acquired immunodeficiency syndrome (AIDS)?
- Why do some small populations differ genetically from their neighbors to such an extent?
- What impact does geography have on our choice of mates?
Even this short list shows that population genetics has relevance to many questions about human biological variation and evolution. In addition, the general principles of population genetics are used to address the same concerns—variation and evolution—in all organisms. In short, population genetics is a key to understanding life. Although this book focuses on human populations (because of my interests and training), never forget that many of the general principles of population genetics apply across the span of life itself.
As noted earlier, the study of human population genetics examines the application of mathematical principles and models to the transmission of genetic information from one generation to the next in human populations. Population genetics can be regarded here as a field that combines genetics, mathematics (especially probability), and anthropology. The remainder of this introductory chapter provides a brief review of some basic principles of genetics and probability, and concludes with a broader consideration of how population genetics applies in an anthropological context.
Considering the nature of this book and its intended audience, one might assume that you are a student in a course on population genetics or a related field. Typically, such students have had some background in some basic concepts of genetics, particularly Mendelian genetics, from high school as well as in an introductory college course in biology or biological anthropology. As such, the following information is not meant to be a detailed discussion of genetics, but instead a brief review of some high points and terminology in order to dive into population genetics as quickly as possible. More detail will be given as needed throughout the text. If you find that the following brief review is a bit too brief, I suggest getting more review and/or detail from comprehensive Internet sources such as Wikipedia, browsing through some introductory genetics books, and consulting with your professor.
Most discussions of genetics start with mention of deoxyribonucleic acid (DNA), often referred to casually as “the genetic code.” Although we are learning more every day about the nature of DNA and how it works, many of the basic principles of population genetics were derived long before much was known about DNA. Indeed, James Watson and Francis Crick discovered the biochemical structure of DNA in 1953, whereas many ideas in population genetics were first developed in the 1930s and 1940s. Although advances in molecular genetics have certainly affected continued development of population genetics in terms of both theory and methods (as will be described later), many of the basic concepts of genetic transmission in populations were developed before we really knew the structure and function of exactly what was being transmitted.
The DNA molecule is made up of two strands that consist of nucleotides, molecules that contain a nitrogen base connected to sugar and phosphate groups. There are four different bases in DNA: adenine (A), thymine (T), cytosine (C), and guanine (G). The sequence of these four different bases make up the genetic “code,” and by analogy they can be considered “letters” in a four-letter DNA alphabet. A related molecule, ribonucleic acid (RNA), is involved in the transcription of proteins, expression of genes, and other vital biochemical functions. A critical aspect of DNA is that the A and T bases pair up as do the C and G bases. As DNA is double-stranded, this means that an A on one strand is paired with a T on the other strand. Likewise, T is paired with A, C with G, and G with C. This property of DNA allows it to make copies of itself, thus ensuring the transmission of genetic information from cell to cell. The pairing of bases between the two stands is known as a base pair (abbreviated bp), and the length of DNA sequences is measured by the number of base pairs.
1.2.1 Mendel’s Laws
Much (though not all) of our DNA exists on long strands in the nuclei of our cells, called chromosomes. Chromosomes come in pairs. Different species have different numbers of chromosomes; humans have 23 pairs, whereas chimpanzees (our closest living relative) have 24 pairs. During the replication of body cells through mitosis, a single cell containing 23 pairs of chromosomes will duplicate, giving rise to two identical cells, each with 23 pairs of chromosomes. However, this is not what happens during reproduction. Instead of passing along 23 pairs of chromosomes to your offspring in a sex cell (sperm in males, egg in females), you pass on one of each pair through the process of meiosis. The process of chromosome pairs separating through meiosis is also known as Mendel’s law of segregation (or, sometimes, as Mendel’s first law). You contribute 23 chromosomes (but not 23 pairs), and your mate contributes 23 chromosomes, resulting in your child having 23 + 23 = 23 chromosome pairs. Likewise, your genetic inheritance also resulted from this process, as one of each chromosome pair came from your mother and the other one came from your father.
As a bisexual organism (a species that has two distinct sexes, male and female), half of your genetic inheritance comes from your mother and half from your father. The same applies to any biological siblings. Apart from identical twins, why are you not genetically identical to a sibling? If my brother and I both received 50% of our DNA from our mother and 50% from our father, why are we not genetically the same? The answer relates to basic probability; we do not inherit the same 50%. For any given chromosome pair, there is a 50 : 50 chance of one being passed on to an offspring, either the maternal chromosome (from your mother) or the paternal chromosome (from your father). For example, imagine that I have passed along my maternal chromosome for the first chromosome pair to a child. The next child may or may not receive the same maternal chromosome; it is a 50 : 50 chance for either the maternal or the paternal chromosome. The same probability applies to each chromosome pair, as they are all independent such that whatever chromosome you pass on from the first chromosome pair has no effect on the second pair, the third, and so on.
We can illustrate this principle with a simple analogy using coins. Imagine an organism with only three chromosome pairs, each represented by a penny with two sides—heads and tails. If we flip the first coin, we have a 50 : 50 chance of getting heads (H) or tails (T). We will use this as a model for a chromosome pair consisting of one chromosome labeled H and one labeled T. If you flip heads for the first coin (chromosome pair), what is the probability of flipping heads on the second coin? It is still 50 : 50 because the coin flips are independent; the outcome of one coin flip does not influence any other coin flips. In terms of the genetic analogy, this hypothetical organism can produce eight different combinations of coin flips. One of these eight combinations would be getting heads for the first coin, heads for the second coin, and heads for the third coin. Another possibility would be heads for the first coin, heads for the second coin, and tails for the third coin. If we follow this pattern, we wind up with eight different combinations, each equally likely:
1. Heads–heads–heads
2. Heads–heads–tails
3. Heads–tails–heads
4. Heads–tails–tails
5. Tails–heads–heads
6. Tails–heads–tails
7. Tails–tails–heads
8. Tails–tails–tails
Because of chance, this organism could produce eight different combinations of chromosomes. This independent inheritance is known as Mendel’s law of independent assortment (or Mendel’s second law).
In principle, we could simulate the same process for human beings by using 23 different coins, but it take much too long to enumerate all possible combinations of coin flips. Instead, we can figure out the number of possibilities using the simple formula 2n, where n is the number of coins/chromosome pairs. For humans, n = 23 chromosome pairs, giving 223 = 8, 333, 608 combinations! Keep in mind that this is for one individual. The same rule applies to the production of sex cells in the individual’s mate; they, too, can produce up to 8,388,608 combinations. A child could therefore have any of the first parent’s combinations paired with any of the second parent’s combinations, giving a total of 8, 388, 608 × 8, 388, 608 = 70, 368, 744, 177, 664 possible genetic combinations in any given child! Given the number of possibilities, it is easy to see why it would be virtually impossible for me to be genetically identical to my nontwin brother for my entire genome.
As is typically the case when explaining basic models of reality, I have to point out that all of the above is actually a bit of an oversimplification. The basic process is further complicated by recombination, which involves the crossover of sections of DNA of chromosome pairs during meiosis. Start with a pair of chromosomes, with one chromosome from the mother and one from the father. During meiosis, the pair does no segregate exactly, such that pieces of the mother’s DNA are exchanged with pieces of the father’s DNA. Thus, any sex cell that you pass on to an offspring is unlikely to follow the ideal Mendelian model of being either your mother’s chromosome or your father’s chromosome, but instead reflects parts of both. The process of recombination provides even more shuffling of genetic combinations with each generation.
Through meiosis with recombination, a new generation can reflect different combinations of what was present in the parental generation. However, in terms of the overall genetic composition of the population (how many different genetic forms exist), this reshuffling does not change anything. An analogy here would be a deck of cards. Each time you shuffle the deck and deal out a five-card poker hand, you are likely to get a different combination, such as a three of clubs, five of spades, six of spades, ten of hearts, and a queen of diamonds. Return these cards to the deck, shuffle, and deal again. You are most likely to have a completely different hand (it is possible to get the same hand, but extremely unlikely, as there are 2,598,960 possible different five-card poker hands using 52 cards and no jokers). Each time you shuffle and deal, you can get a new combination, but the basic composition of the deck has not changed—you still have four suits each with 13 cards ranging from 2 through ace. Nothing new would happen unless there were a mutation in the deck, say, resulting from changing a 10 of spades to a brand new type of card, such as an 11 of spades. (Don’t try this in a real game!) Population genetics involves understanding how the genetic composition of a population can change through the operation of mutation and other forces of evolution.
1.2.2 Alleles, Genotypes, and Phenotypes
What is a gene? As with many core ideas and concepts (e.g., life, love, culture, race), the actual definition of gene has changed over time and is often difficult to pin down (Marks and Lyles 1994). The term gene was first used in a very general way to refer to a unit of inheritance. With the growth of molecular genetics, it has become more common to refer to a gene in a more specific sense, which is a DNA sequence associated with a functional product, such as a protein. This more restricted definition does not include noncoding sections of DNA. Although some population geneticists use the more current restricted definition (e.g., Hamilton 2009), others use the more general definition for convenience (e.g., Hedrick 2005). Here, I will use the more specific restricted definition to comply with your likely background in genetics, and refer to the entire genome as consisting of genes and other DNA sequences. The broader term genetic marker is often used to refer to any gene or DNA sequence that has a known location on a specific chromosome.
When we study a genetic marker, we refer to its specific location on a particular chromosome; this location is referred to as a locus (plural loci). A key concept in population genetics is the allele, which refers to alternative forms of a gene or DNA sequence at a given locus. Loci that have two or more alleles that are not rare (typically defined as a frequency greater than 0.01) are called polymorphisms, which literally translates as “many forms.”
As an example of the concept of allele, consider the gene that affects lactase production in humans. As mammals, humans rely on milk during infancy. We produce an enzyme (lactase) in order to break down milk sugar (lactose). A specific gene (LCT) is located on chromosome 2 and regulates the production of lactase. There are several different forms (alleles) of this gene. One allele (R) causes enzyme production to decrease during early childhood (an age by which humans have been weaned), and another allele (P) allows continued high production of lactase into adulthood, a condition known as lactase persistence. There is also a third rare allele, but it will not be discussed in this example (Mielke et al. 2011).
For any trait in your nuclear DNA, including lactase activity, you inherit two copies of the gene or DNA sequence, one from your mother and one from your father, which collectively makes up your genotype. In the case of lactase activity, there are two main alleles (R and P) in the human species, which means that there are three possible genotypes. Some individuals will inherit two copies of the P allele and will have the genotype PP, while others will inherit two copies of the R allele and have the RR genotype. Both people with PP and RR genotypes are homozygous for this trait, which means that they have inherited the same allele from both mother and father. There is a third possibility, which is the genotype PR, where the person has inherited a P allele from one parent and an R allele from another parent (it does not matter which parent gave the P allele and which gave the R allele). When someone inherits a different allele from each parent, that person is heterozygous for that trait.
What are the different outcomes for these different genotypes? Each has inherited genetic information regarding the restriction or persistence of lactase production. The physical manifestation of a genotype is known as the phenotype. In complex traits, such as height or skin color, the phenotype is a reflection of the genotypes of the different genes that affect the trait as well as environmental effects, such as nutrition in the case of height, or solar exposure in the case of skin color. In “simple” genetic traits, such as lactase activity, the phenotype is determined by the genotype and which, if any, alleles are dominant or recessive. The effect of a dominant allele is noticeable even if only one copy is present, whereas a recessive allele’s effect can be masked by a dominant allele. In the case of lactase activity, the P allele (lactase persistence) is dominant and the R allele (restriction) is recessive. This means that someone who inherits one or two P alleles will show the lactase persistence phenotype, and those that inherit two R alleles will show lactase restriction. In other words, lactase persistence can result from either the PP or PR genotypes, and lactase restriction can result only from having the RR genotype.
It is important to remember that dominant and recessive refer to the nature of the alleles and have nothing to do with the actual frequency of an allele; that is, a dominant allele is not necessarily more common than a recessive allele. For example, in humans there is a condition resulting in extra fingers or toes (polydactyly) that is caused by a dominant allele, yet it is very rare in occurrence (Wolf and Myrianthopoulos 1973). Another example in humans is the ABO blood group, where the most common allele in our species is the O allele, which is recessive.
For any given locus, the alleles need not be either dominant or recessive. For many loci, the alleles are codominant, meaning that the effect of both alleles is expressed in the phenotype. An example in humans is the MN blood group located on chromosome 4, which has two alleles, M and N, which produce different molecules on the surface of our red blood cells; the M allele produces type M molecules and the N allele produces type N molecules. Given these two alleles, we have three possible genotypes: MM, MN, and NN. What about the phenotypes? Logically, we can see that the homozygous genotype MM will result in type M molecules because both alleles contain the same message—type M blood. It is also clear that the genotype NN will produce type N molecules. What of the genotype MN? The phenotype associated with a heterozygous genotype depends on whether one allele was dominant. In this case, the M and N alleles are codominant, which means that both the M allele and the N allele will manifest, resulting in the production of both type M and type N molecules. In the case of a codominant locus, each genotype has a distinct phenotype. As we will see in Chapter 2, this makes it much easier to count alleles and determine their frequency (a vital part of population genetics).
Before moving on, I want to point out some other complications. Although most examples in this book use a simple model of a single locus with two alleles, in reality there are actually many loci with more than two alleles, and some loci where there are dozens of alleles. Basic concepts will be introduced using the simple two-allele model where possible and bringing in this additional complication where appropriate.
Another complication is the fact that some loci have dominant, recessive, and codominant alleles. A good example for humans is the ABO blood group, located on chromosome 9. There are three main alleles, A, B, and O, where the A allele codes for type A molecules, the B allele codes for type B molecules, and the O allele codes for neither of these. In the ABO system, the O allele is recessive and the A and B alleles are codominant. Given three possible alleles, there are six possible genotypes: AA, BB, OO, AO, BO, and AB. What are the possible phenotypes?
The phenotypes of the three homozygous genotypes (AA, BB, and OO) are easy to determine. Genotype AA produces type A blood, genotype BB produces type B blood, and genotype OO produces type O blood. The phenotypes of the three remaining genotypes can be determined by knowing which alleles are dominant, recessive, or codominant. Because the O allele is recessive, those with genotype AO will show only the effect of the dominant A allele, and hence will have type A blood. Likewise, those with genotype BO will show only the effect of the dominant B allele, and will have type B blood. The remaining genotype, AB, has two codominant alleles, which means that both A and B molecules will be produced, and people with this genotype therefore have what we call type AB blood. For the ABO blood group, there are three alleles that can form six different genotypes that correspond to four different phenotypes (ignoring for the moment additional complications, such as the fact that there are actually two subtypes of the A allele).
1.2.3 How Do We Assess Human Genetic Diversity?
As will be clear in later chapters, much of the core of population genetics theory is abstract, dealing with hypothetical alleles at hypothetical loci in hypothetical populations. Although hypothetical rumination is interesting in and of itself, the ultimate test of a mathematical model of reality is to see how well it represents reality, which means that at some point we need information about real alleles at real loci in real populations! Although a variety of loci and traits will be provided in case studies throughout this book, it is useful to look briefly at some of the different ways anthropologists and geneticists use to assess genetic diversity.
1.2.3.1 Red Blood Cell Markers
For the first half of the twentieth century, most information on genetic diversity in human populations came from the study of blood types based on red blood cell groups, where phenotypes were based on the reaction of antigens present in the blood with corresponding antibodies (Boyd 1950). In the ABO blood group system, for example, this is based on reactions of A and B antigens with their respective antibodies, anti-A and anti-B. Suppose that someone’s blood shows a reaction with the anti-A antibody but not the anti-B antibody. This means that they have the A antigen but not the B antigen, and therefore have blood type A, and therefore either the AA or the AO genotype. There are many different red blood cell systems, including ABO, Rhesus, MN, Kell, Diego, Duffy, and P (Crawford 1973).
By the 1960s and 1970s, technological advances such as electrophoresis had led to a proliferation of other genetic markers of the blood. Electrophoresis involves passing an electric current through a gel. Blood samples are placed at the negative pole of the gel and, as current flows from negative to positive, molecules move through the gel. Because different molecular structures move at different rates, the process allows identification of different molecular structures associated with different genotypes. Applied to blood samples from anthropological surveys, a vast amount of data were collected on numerous red blood cell protein and enzyme loci (Crawford 1973; Roychoudhury and Nei 1988; Cavalli-Sforza et al. 1994).
1.2.3.2 DNA Markers
Genetic markers of the blood, including markers based on white blood cells, are now labeled as classical genetic markers, contrasted with the newer DNA markers. Although classical markers provide information on genetic variation, DNA markers provide a closer window on genetic variation, moving beyond the level of molecular variability to the underlying level of DNA variation.
One method of DNA analysis involves the identification of restriction fragment length polymorphisms (RFLPs). Restriction enzymes that are produced by different types of bacteria can bind to sections of a DNA sequence and cut that sequence at a particular point. For example, the EcoRI bacterial enzyme will bind to the 6-bp sequence GAATCC (which, by definition, corresponds to the sequence CTTAGG on the other DNA strand). If this sequence is present in a DNA sample, EcoRI will cut the sequence between the G and the first A, producing two fragments, one with the base G and the other with the sequence AATCC. If the DNA sample did not contain the sequence GAATCC, but instead had a mutation resulting in GATTCC (where the second A mutated into T), then the target sequence would not be recognized and the DNA sample would not be cut. Depending on the presence or absence of certain DNA sequences, a DNA sample might be cut into fragments of different lengths.
Another type of DNA variation widely studied in human populations consists of repeated DNA sequences, such as CACACACACACACA, where the 2-bp sequence is repeated 7 times. Because of mutation, the number of repeats can go up or down, resulting in variation. Short tandem repeats (STRs), also known as microsatellite DNA, are widely used in studies of human populations. STRs consist of short repeated sequences consisting of 2–5 bp. Longer repeated sequences, known as minisatellites, are also used.
Another form of DNA analysis looks for single-nucleotide polymorphisms (SNPs), where DNA sequences differ by one base, such as having the base C on one sequence versus the base T on another sequence:
Sequence 1: TATTCCGGA
Sequence 2: TACTCCGGA
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


