[2]. A PET camera detects many of these 511 keV photon pairs in coincidence. These pairs are then assigned to lines of response (LOR) which are used in the image reconstruction process to yield a tomographic 3D image of the tracer distribution in the human body. The concept of PET photon creation and collection is sketched in Fig. 28.1. Due to the finite width of the pixel elements, the LORs are actually tubes-of-response. The width of these tubes is related to the spatial resolution of the system.
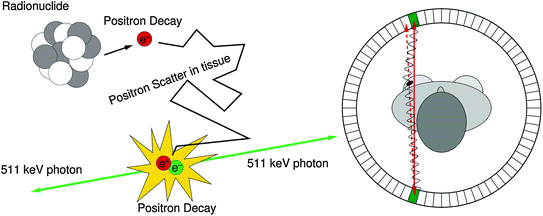
Fig. 28.1
Left The mechanism for signal generation in PET: a positron is emitted by a proton rich nucleus. After thermalization, the positron annihilates with an electron from the surrounding medium, resulting in the emission of two 511 keV photons back-to-back. Right The solid red line is an observed line of response (LOR) in a PET camera, obtained by combining the interaction locations of the two 511 keV photons. If the center of mass momentum of the positron and electron is nonzero in the lab reference frame when they annihilate, the photons have a slight acolinearity. The dashed red line is the true LOR
In order to obtain high-quality images, contrast needs to be enhanced as much as possible, e.g. by reducing background present in PET images. There are two main background mechanisms in PET: scatter and random coincidences, schematically shown in Fig. 28.2.
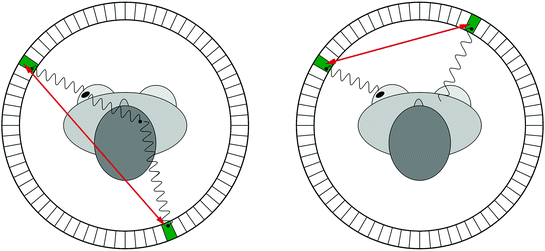

Fig. 28.2
Object scatter (left) and random coincidences (right) cause positioning errors that reduce image contrast and quantitative accuracy
Since a scattered photon will have lost some energy, object scatter can be identified by measuring the energy of the detected photon accurately. Therefore, it is desirable for a PET camera to have excellent energy resolution.
A random coincidence occurs when two photons, each originating from a different location, are assumed to be part of the same pair. This will happen, for instance, when only one of the two annihilation photons is detected, a situation that may happen frequently given the limited coincidence photon detection sensitivity of PET cameras. The number of random coincidences is reduced by utilizing a smaller coincidence time window, which is the time during which a PET system considers two photons as being simultaneously emitted. PET cameras with a fine time resolution allow for tighter coincidence windows and less random coincidence background.
Newer systems with time resolution <1 ns are able to use timing information to assign probabilities to where along the line of response the tracer was emitted, yielding “time-of-flight” (TOF) PET, which we will come back to later in this chapter (Sect. 28.6).
In order to precisely localize the tracer distribution, PET cameras should also have a fine spatial resolution, preferably uniform across the field of view (FOV).
A fourth requirement for a PET camera is high sensitivity to detect emitted radiation. This efficiency can be expressed as a product of a geometric form factor 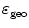 and an intrinsic detection efficiency
and an intrinsic detection efficiency 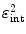 . The former depends on the solid angle coverage of the detection elements, which in term depend on the system form factor and the packing fraction of the active detector elements.
. The former depends on the solid angle coverage of the detection elements, which in term depend on the system form factor and the packing fraction of the active detector elements. 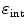 on the other hand measures the efficiency to detect an incident 511-keV photon and depends on the
on the other hand measures the efficiency to detect an incident 511-keV photon and depends on the 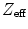 and the density and thickness of the detector material. Since PET requires coincident photon detection, the intrinsic detection efficiency needs to be squared.
and the density and thickness of the detector material. Since PET requires coincident photon detection, the intrinsic detection efficiency needs to be squared.
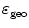 and an intrinsic detection efficiency
and an intrinsic detection efficiency 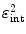 . The former depends on the solid angle coverage of the detection elements, which in term depend on the system form factor and the packing fraction of the active detector elements.
. The former depends on the solid angle coverage of the detection elements, which in term depend on the system form factor and the packing fraction of the active detector elements. 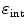 on the other hand measures the efficiency to detect an incident 511-keV photon and depends on the
on the other hand measures the efficiency to detect an incident 511-keV photon and depends on the 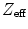 and the density and thickness of the detector material. Since PET requires coincident photon detection, the intrinsic detection efficiency needs to be squared.
and the density and thickness of the detector material. Since PET requires coincident photon detection, the intrinsic detection efficiency needs to be squared.Since the contrast mechanism in PET images is mainly caused by biochemical activity, it is often difficult to localize regions of high focal uptake relative to anatomical landmarks that show little or no tracer uptake such as the organs and skeleton in a patient’s body. The combination of a PET camera with an X-ray computed tomography (CT) camera results in a hybrid PET/CT image and enables precise localization of areas with high tracer uptake. In addition, the CT camera can be used for calculating an attenuation correction, i.e. a compensation for the nonuniform attenuation of 511-keV photons in the different tissues of the human body. Attenuation correction results in higher-quality images. Another advantage of this dual modality is the confirmation of suspicious lesions on both PET and CT images, hence, reducing the number of false-positive lesions. The combination of PET and CT camera is currently considered the best imaging modality in oncologic settings [3, 4].
The number of PET/CT procedures in the clinic has steadily been increasing since the introduction of this modality around the start of the millennium. The volume of studies increased by 7.1 % between 2008 and 2010 in the United States. In 2011, 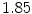 million patient studies were performed at 2,209 sites, up from 2,000 sites in 2008 [5]. The number of PET only sites decreased from 215 to 120 over the same period. In 2012, 94 % of the PET/CT procedures were oncology related, 3 % cardiology related, and 3 % in neurology. In oncology, 68 % of procedures are for lung, breast, lymphoma, and colorectal cancer. Among these, 19 % is used for diagnosis, 38 % for staging, 13 % for treatment planning, and 30 % therapy follow-up. The increased availability of PET/CT cameras resulted in a reduced wait time from 7 to 4 days [5].
million patient studies were performed at 2,209 sites, up from 2,000 sites in 2008 [5]. The number of PET only sites decreased from 215 to 120 over the same period. In 2012, 94 % of the PET/CT procedures were oncology related, 3 % cardiology related, and 3 % in neurology. In oncology, 68 % of procedures are for lung, breast, lymphoma, and colorectal cancer. Among these, 19 % is used for diagnosis, 38 % for staging, 13 % for treatment planning, and 30 % therapy follow-up. The increased availability of PET/CT cameras resulted in a reduced wait time from 7 to 4 days [5].
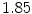 million patient studies were performed at 2,209 sites, up from 2,000 sites in 2008 [5]. The number of PET only sites decreased from 215 to 120 over the same period. In 2012, 94 % of the PET/CT procedures were oncology related, 3 % cardiology related, and 3 % in neurology. In oncology, 68 % of procedures are for lung, breast, lymphoma, and colorectal cancer. Among these, 19 % is used for diagnosis, 38 % for staging, 13 % for treatment planning, and 30 % therapy follow-up. The increased availability of PET/CT cameras resulted in a reduced wait time from 7 to 4 days [5].
million patient studies were performed at 2,209 sites, up from 2,000 sites in 2008 [5]. The number of PET only sites decreased from 215 to 120 over the same period. In 2012, 94 % of the PET/CT procedures were oncology related, 3 % cardiology related, and 3 % in neurology. In oncology, 68 % of procedures are for lung, breast, lymphoma, and colorectal cancer. Among these, 19 % is used for diagnosis, 38 % for staging, 13 % for treatment planning, and 30 % therapy follow-up. The increased availability of PET/CT cameras resulted in a reduced wait time from 7 to 4 days [5].The vast majority (96 %) of PET studies use fluoro-deoxyglucose (FDG) as a tracer, which is a glucose analog, where the 2′ OH group is replaced by 18F. Due to the enhanced anaerobic sugar metabolism of cancer cells (i.e., the Warburg effect, see, e.g., [6]), FDG molecules preferably accumulate in these cells. Due to the lack of the 2′ OH group, FDG cannot be fully metabolized, and thus, remains in these cells until 18F decays into 18O. In addition, the 110 min half-life of 18F makes the isotope practical for use in the clinic. Other tracers are, for example, 82Rb for myocardial studies [7] and 11C labeled PiB (Pittsburg compound B) for beta-amyloid imaging [8], in the quest to predict and diagnose early appearance of Alzheimer’s disease. A large number of other tracers have been developed or are under study [9].
The development of disease-specific tracers could potentially yield enhanced contrast in PET images due to the higher specific uptake. This would result in higher-quality images without significant improvement in instrumentation. It is also likely that patient dose can be reduced by development of very specific tracers. However, it is important as well to note that the fact that the Warburg effect is present in most cancer cells has resulted in the success and usability of FDG-PET in the clinic.
Over the last two decades, large progress has been made in the development of PET cameras. Both clinical as well as preclinical (small animal) PET cameras have improved spatial, energy, and time resolution, resulting in reliable visualization and quantification of smaller tumors. A general paradigm in medicine is that earlier detection of smaller lesions results in better patient outcome. In addition, improved spatial resolution enables improved monitoring of the effects of radio- or chemotherapy, which often show up earlier on PET images than the corresponding CT images. This chapter discusses the potential improvements in PET detectors that can be implemented in the next-generation PET cameras and will result in better image quality. In order to discuss these improvements, we start with a description of the current generation. Throughout the chapter, we will only focus on the improvement of the PET detectors. We refer the reader to the literature to study improvements in CT images.
28.2 Current-Generation Commercially Available PET Cameras
It is instructive to look at the performance of current commercially available state-of-the-art PET/CT cameras by the leading manufacturers Philips, Siemens, and GE Healthcare. All three manufacturers use a traditional “block-detector” scheme for their cameras: a scintillation crystal is used to stop and convert the 511-keV photons into many optical photons, which are then converted to electronic charge using a photomultiplier-tube (PMT). The charge is further digitized and processed by data acquisition (DAQ) boards and stored to disk. A “block detector” typically consists of an array of PMTs coupled to a segmented scintillation crystal. In these, the number of PMTs is smaller than the number of crystal elements. The segmentation is optimized to maximize interaction location resolvability. Figure 28.3 shows a photograph of a typical block detector along with a schematic of the interaction process.
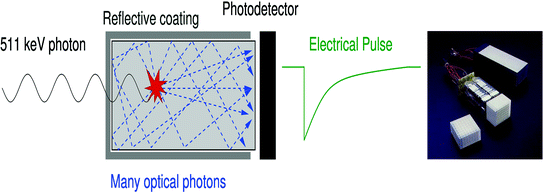

Fig. 28.3
Left Optical photons are created in a scintillation crystal upon absorption of a 511-keV photon. After a number of reflections, the optical photons reach the photodetector where they are converted into electric charge. Right A block detector in a standard PET camera. An 8 × 8 scintillation crystal array (lower left corner) is coupled to 4 PMTs (middle) and placed in a specially designed housing (upper right corner). Figure courtesy of Siemens Healthcare
Table 28.1 gives an overview of hardware configuration and associated performance of state-of-the-art cameras. We see that all manufacturers have a similar axial field-of-view (FOV) of about 16–18 cm. The Siemens biograph comes with a TrueV (sic) option, which allows an extended axial FOV. Array crystal element size is typically 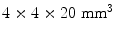 , resulting in about 25,000 crystal elements per camera. The GE design uses a slightly larger crystal resulting in about 14,000 crystals in the entire camera. Acquisition time is about 15–40 min. The scintillation material used by all manufacturers is Lutetium based, with an unspecified “lutetium-based scintillator” for GE, and LYSO and LSO for Philips and Siemens, respectively. These specifications are readily available on the manufacturer’s website.
, resulting in about 25,000 crystal elements per camera. The GE design uses a slightly larger crystal resulting in about 14,000 crystals in the entire camera. Acquisition time is about 15–40 min. The scintillation material used by all manufacturers is Lutetium based, with an unspecified “lutetium-based scintillator” for GE, and LYSO and LSO for Philips and Siemens, respectively. These specifications are readily available on the manufacturer’s website.
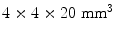 , resulting in about 25,000 crystal elements per camera. The GE design uses a slightly larger crystal resulting in about 14,000 crystals in the entire camera. Acquisition time is about 15–40 min. The scintillation material used by all manufacturers is Lutetium based, with an unspecified “lutetium-based scintillator” for GE, and LYSO and LSO for Philips and Siemens, respectively. These specifications are readily available on the manufacturer’s website.
, resulting in about 25,000 crystal elements per camera. The GE design uses a slightly larger crystal resulting in about 14,000 crystals in the entire camera. Acquisition time is about 15–40 min. The scintillation material used by all manufacturers is Lutetium based, with an unspecified “lutetium-based scintillator” for GE, and LYSO and LSO for Philips and Siemens, respectively. These specifications are readily available on the manufacturer’s website.Table 28.1
Hardware and performance parameters of state-of-the-art commercially available PET/CT cameras
Philips | Siemens | GE | ||
|---|---|---|---|---|
TruFlight | Biograph TruePoint | Discovery 710 | ||
Hardware | ||||
Axial FOV | cm | 18 | 16.2 (21.6)a | 15.7 |
Number of crystals | 28,336 | 24,336 (32,448)a | 13,824 | |
Number of PMTs | 420 | 576 (768)a | 256b | |
Detector material | LYSO | LSO | LBSc | |
Crystal size | mm3 | 4 × 4 × 22 | 4 × 4 × 20 | 4.2 × 6.3 × 25 |
Acquisition time | min | 15 | 20 (10)a | N.A. |
NEMA performance | ||||
Sensitivity center | cps/kBq | 4.5 | 4.4(7.9)a | 7 |
Transverse spatial resolution @1 cm | mm | 4.7 | 4.4 | 4.9d |
Transverse spatial resolution @10 cm | mm | 5.2 | 4.9 | 6.3d |
Axial spatial resolution @1 cm | mm | 4.7 | 4.5 | 5.6d |
Axial spatial resolution @10 cm | mm | 5.2 | 5.9 | 6.3d |
Peak NECR | kcps@kBq/ml | 65@20 | 96@25(165@35)a | 130@19.5 |
The National Electrical Manufacturers Association (NEMA) defined procedures for evaluating performance of PET systems in order to standardize these [10]. The sensitivity, as measured by these NEMA standards, varies between 0.5 and 0.7 % (=5 – 7 counts per second (cps)/kBq), thus smaller than 1 % for all systems. Transaxial spatial resolution is about 4.4–5.2 mm, with slightly inferior axial resolution for the GE system due to the use of rectangular cross-sectional crystal elements. In the most recent systems, all manufacturers have omitted the use of septa to increase sensitivity. All systems acquire data in 3D.
28.3 Progress for Scintillation Crystals
This section covers the progress towards improving the active detector elements in PET cameras, which are responsible for absorbing and converting the 511-keV annihilation radiation. We first cover the more traditional method of using scintillation crystals. We will discuss various modern crystal types, the configuration of these in so-called block detectors, and progress on light extraction methods. A discussion on photodetectors coupled to these scintillators is given in Sect. 28.4. We will discus semiconductor detectors, which directly convert the incident photon into electric charge, in Sect. 28.5.
28.3.1 Scintillation Crystals
An optimal scintillation crystal for a PET camera should have a high stopping power for 511 keV photons, a high light yield, fast rise and fall time, and a fine energy resolution. In order to increase sensitivity, it is desirable to have crystals with a high density and a high atomic number Z (or 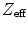 ). A high light output is desirable in order to increase the signal from the detector, which facilitates event positioning methods and moderates the requirements on the readout electronics. The energy resolution of typical scintillation crystals is only indirectly related to the light output: given the roughly 10,000 photons created in LSO upon 511 keV photoelectric absorption, one would expect a variation of about 1 % when using Poisson counting statistics alone. Due to the nonproportionality of the scintillation process [14], the energy resolution for LSO crystals is not better than 9 % FWHM at 511 keV. Nonproportionalities in light output as a function of energy may become more important if lower-energy detector scatter events are included in the event-list. Currently, the detector response is often assumed linear and calibration is done using the 511-keV photopeak position.
). A high light output is desirable in order to increase the signal from the detector, which facilitates event positioning methods and moderates the requirements on the readout electronics. The energy resolution of typical scintillation crystals is only indirectly related to the light output: given the roughly 10,000 photons created in LSO upon 511 keV photoelectric absorption, one would expect a variation of about 1 % when using Poisson counting statistics alone. Due to the nonproportionality of the scintillation process [14], the energy resolution for LSO crystals is not better than 9 % FWHM at 511 keV. Nonproportionalities in light output as a function of energy may become more important if lower-energy detector scatter events are included in the event-list. Currently, the detector response is often assumed linear and calibration is done using the 511-keV photopeak position.
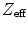 ). A high light output is desirable in order to increase the signal from the detector, which facilitates event positioning methods and moderates the requirements on the readout electronics. The energy resolution of typical scintillation crystals is only indirectly related to the light output: given the roughly 10,000 photons created in LSO upon 511 keV photoelectric absorption, one would expect a variation of about 1 % when using Poisson counting statistics alone. Due to the nonproportionality of the scintillation process [14], the energy resolution for LSO crystals is not better than 9 % FWHM at 511 keV. Nonproportionalities in light output as a function of energy may become more important if lower-energy detector scatter events are included in the event-list. Currently, the detector response is often assumed linear and calibration is done using the 511-keV photopeak position.
). A high light output is desirable in order to increase the signal from the detector, which facilitates event positioning methods and moderates the requirements on the readout electronics. The energy resolution of typical scintillation crystals is only indirectly related to the light output: given the roughly 10,000 photons created in LSO upon 511 keV photoelectric absorption, one would expect a variation of about 1 % when using Poisson counting statistics alone. Due to the nonproportionality of the scintillation process [14], the energy resolution for LSO crystals is not better than 9 % FWHM at 511 keV. Nonproportionalities in light output as a function of energy may become more important if lower-energy detector scatter events are included in the event-list. Currently, the detector response is often assumed linear and calibration is done using the 511-keV photopeak position.Another increasingly important parameter for scintillation crystals is their rise and decay time. These are important because they impose fundamental limits on the coincidence timing resolution of PET detectors. While the rise time is experimentally difficult to assess, it is of great importance to the time resolution [15]. Rise time optimization will likely yield to improved timing resolution as we will discuss in Sect. 28.6.
The peak emission wavelength of scintillation crystals for PET detectors should match the maximum quantum efficiency (QE) of the photon detector, in order to increase signal output. Matching of the index of refraction of the scintillator to the photodetector entrance window is important as well in order to reduce reflective losses and hence to maximize the signal.
Table 28.2 gives an overview of a number of scintillation detectors and their properties. BGO used to be a popular choice, because of its high 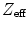 and relatively high density, yielding a large photon detection efficiency (PDE). However, due to its poor decay time, moderate light output, and high index of refraction, it has been replaced by LSO or LYSO in many recently constructed cameras. LYSO has similar properties to LSO and is not included in the table. It is instructive to see that calcium co-doping in LSO yields a better energy resolution and a faster decay time [16], indicating that dopant concentration is very important for scintillator performance.
and relatively high density, yielding a large photon detection efficiency (PDE). However, due to its poor decay time, moderate light output, and high index of refraction, it has been replaced by LSO or LYSO in many recently constructed cameras. LYSO has similar properties to LSO and is not included in the table. It is instructive to see that calcium co-doping in LSO yields a better energy resolution and a faster decay time [16], indicating that dopant concentration is very important for scintillator performance.
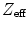 and relatively high density, yielding a large photon detection efficiency (PDE). However, due to its poor decay time, moderate light output, and high index of refraction, it has been replaced by LSO or LYSO in many recently constructed cameras. LYSO has similar properties to LSO and is not included in the table. It is instructive to see that calcium co-doping in LSO yields a better energy resolution and a faster decay time [16], indicating that dopant concentration is very important for scintillator performance.
and relatively high density, yielding a large photon detection efficiency (PDE). However, due to its poor decay time, moderate light output, and high index of refraction, it has been replaced by LSO or LYSO in many recently constructed cameras. LYSO has similar properties to LSO and is not included in the table. It is instructive to see that calcium co-doping in LSO yields a better energy resolution and a faster decay time [16], indicating that dopant concentration is very important for scintillator performance.BGO | GSO:Ce | LSO:Ce | LSO:Ca | LaBr3:Ce | LuAP:Ce | LuAg:Pr | LuI3 | ||
|---|---|---|---|---|---|---|---|---|---|
Formula | Bi4Ge3O12 | Gd2SiO5:Ce | Lu2SiO5:Ce | Lu2SiO5:Ca | LaBr3:Ce | LuAlO3:Ce | Lu3Al5O12:Pr | LuI3:Ce | |
Density |  | 7.13 | 6.71 | 7.40 | 7.40 | 5.29 | 8.34 | 7.4 | 5.68 |
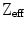 | 75 | 59 | 66 | 66 | 47 | 65 | 63 | 60 | |
Photofraction | @511 keV | 0.44 | 0.26 | 0.34 | 0.34 | 0.13 | 0.32 | 0.29 | 0.22 |
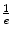 Length PEa Length PEa | cm | 2.5 | 5.7 | 3.6 | 3.6 | 16.3 | 3.5 | 4.4 | 8.7 |
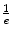 Length all Length all | cm | 1.1 | 1.5 | 1.2 | 1.2 | 2.2 | 1.1 | 1.3 | 1.9 |
Light output | photons/MeV | 8,200 | 12,500 | 27,000 | 29,400 | 57,700 | 16,300 | 18,000 | 115,000 |
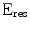 @662 @662 | % FWHM | 10.2 | 9.2 | 8.2 | 6.8 | 2.7 | 10.6 | 5.2 | 3.6 |
Decay time | ns | 300 | 30–60 | 40 | 30 | 18 | 17 | 22 | 33 |
Peak emission | nm | 480 | 430 | 420 | 420 | 356 | 365 | 320 | 505 |
Index of refraction | 2.15 | 1.85 | 1.82 | 1.82 | 1.88 | 1.97 | 1.84 | NA |
LaBr3 has excellent energy resolution and a very short decay time. However, its drawbacks include its poor photofraction and its hygroscopic nature, which makes it necessary to avoid contact with moisture when utilizing this crystal.
LuAP combines a fast decay time with a high density. The latter results in a short attenuation (1/e) length. Using praseodymium (Pr) as the activating dopant instead of cerium (Ce), as in the case of LuAg, results in an improved energy resolution, while maintaining the fast decay. The drawbacks of 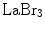 , LuAP, and LuAg are their short emission wavelengths, resulting in tight requirements on the photodetector.
, LuAP, and LuAg are their short emission wavelengths, resulting in tight requirements on the photodetector.
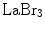 , LuAP, and LuAg are their short emission wavelengths, resulting in tight requirements on the photodetector.
, LuAP, and LuAg are their short emission wavelengths, resulting in tight requirements on the photodetector.Among the newer crystals, 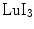 has some interesting properties: very high light yield, excellent energy resolution, a short decay time, and a better attenuation length than
has some interesting properties: very high light yield, excellent energy resolution, a short decay time, and a better attenuation length than 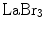 . Its emission wavelength is redshifted which may be beneficial when used with silicon-based photodetectors.
. Its emission wavelength is redshifted which may be beneficial when used with silicon-based photodetectors.
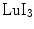 has some interesting properties: very high light yield, excellent energy resolution, a short decay time, and a better attenuation length than
has some interesting properties: very high light yield, excellent energy resolution, a short decay time, and a better attenuation length than 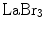 . Its emission wavelength is redshifted which may be beneficial when used with silicon-based photodetectors.
. Its emission wavelength is redshifted which may be beneficial when used with silicon-based photodetectors.As seen from Table 28.1, the big three clinical PET system vendors all choose Lutetium-based crystals, whereas BGO used to be the material of choice. Philips and Siemens use LYSO and LSO respectively, GE uses a nonspecified lutetium-based material. LuAG is currently used in an application-specific PET camera for breast imaging [17].
28.3.2 DOI Configurations
When comparing the newest generation of clinical PET cameras with older ones, we see that there has been a drive to increase spatial resolution by utilizing smaller crystals. Indeed, manufacturers use 4 × 4 mm2 crystals today, compared to 6 × 12 mm2 that was state-of-the-art in 1991 for the GE “4096+” system.
While the area of the crystals has been made smaller over the years, their length has stayed more or less the same in order to maintain sensitivity. As a consequence, spatial resolution of PET cameras only improved in two dimensions. The lack of resolution in the radial dimension (i.e., along an LOR) results in a nonuniform resolution across the FOV. This becomes apparent through increased blurring of point sources when going from center to the edge of a camera. This effect is also known as the parallax error, or LOR blurring and is indicated in Fig. 28.4.
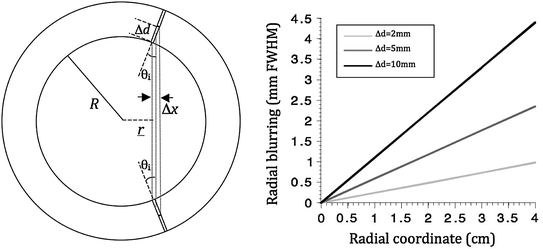

Fig. 28.4
Left shows the coordinates used in Eq. 28.1. Right is a numerical evaluation of the same equation for different DOI resolutions 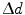
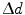
With r the radial coordinate varying between 0 and the ring radius 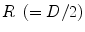 , and
, and 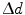 the interaction depth resolution, we obtain
the interaction depth resolution, we obtain
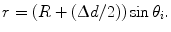
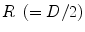 , and
, and 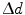 the interaction depth resolution, we obtain
the interaction depth resolution, we obtain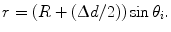
Looking at the figure, the precision in 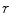 ,
, 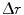 , can now be expressed as
, can now be expressed as
![$$ \begin{aligned} \Updelta r & \approx {\kern 1pt} \Updelta x/2 = (\Updelta d/2)\sin \theta_{i} \quad ({\text{FWHM}}) \\ & = {\kern 1pt} (\Updelta d/2)r/\left[ {R + (\Updelta d/2)} \right] \\ & = {\kern 1pt} r/\left[ {(D/\Updelta d) + 1} \right]. \\ \end{aligned} $$](/wp-content/uploads/2017/03/A305812_1_En_28_Chapter_Equ1.gif)
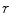 ,
, 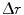 , can now be expressed as
, can now be expressed as![$$ \begin{aligned} \Updelta r & \approx {\kern 1pt} \Updelta x/2 = (\Updelta d/2)\sin \theta_{i} \quad ({\text{FWHM}}) \\ & = {\kern 1pt} (\Updelta d/2)r/\left[ {R + (\Updelta d/2)} \right] \\ & = {\kern 1pt} r/\left[ {(D/\Updelta d) + 1} \right]. \\ \end{aligned} $$](/wp-content/uploads/2017/03/A305812_1_En_28_Chapter_Equ1.gif)
(28.1)
This equation is plotted in the right panel of Fig. 28.4 for different 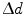 values. We see that the blurring increases when going away from the center of the FOV, and for larger interaction depth resolutions.
values. We see that the blurring increases when going away from the center of the FOV, and for larger interaction depth resolutions.
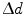 values. We see that the blurring increases when going away from the center of the FOV, and for larger interaction depth resolutions.
values. We see that the blurring increases when going away from the center of the FOV, and for larger interaction depth resolutions.Improving the resolution in the radial dimension by so-called depth-of-interaction (DOI) measurements will increase spatial resolution uniformity across the FOV and yield images with better resolution and contrast.1 Research groups at universities across the globe have been investigating various detector configurations to improve DOI detection. Over the next sections, we will discuss a number of DOI configurations pursued by different research groups. An overview of these is seen in Fig. 28.5. A more comprehensive overview can be found in [26].
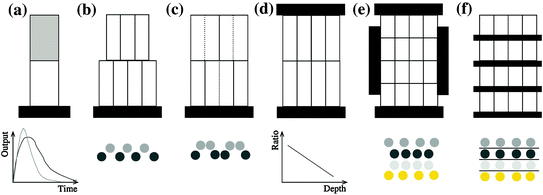

Fig. 28.5
Different DOI designs referred to in the text. a Phoswich; b crystal offset; c light sharing; d dual-ended readout, e and f direct DOI measurement. The bottom row shows how the detector output is used to obtain depth information: a uses different pulse shapes; d uses a ratio between top and bottom detector signals; b, c, e, and f utilize crystal positions in the flood histogram to localize interaction depth: the circles in b, c, e, and f represent the resulting crystal element positions in a flood histogram
28.3.2.1 Pulse Shape Discrimination
One of the first attempts to obtain DOI information was using pulse shape discrimination (PSD): two or more scintillation crystals with different decay times are coupled together. Based on the pulse shape observed, estimations are made whether the interaction happened in the top or the bottom crystal. The design is schematically represented in Fig. 28.5a. These configurations are also known as “phoswich” configurations, a combination of “phosphor” and “sandwich”. Phoswich designs originate from X- and gamma-ray astronomy experiments [27].
The PSD approach is still being investigated as a method to improve DOI in the next-generation scanners. Mosset et al. [28] built an LSO/LuYAP combination which is 98 % efficient in determining the correct interaction location. As shown in simulations by Jung et al. [29], identification may be improved depending on the optical coupling between different crystals. More recently, Vaquero et al. [30] investigated a combination of LYSO and GSO coupled to a matrix of silicon photomultipliers (Si-PMs, see Sect. 28.4.3) and evaluated a delayed charge integration method.
While several research groups have reported low misidentification and high efficiency, the PSD approach has a number of drawbacks. One problem is that the pulse shape needs to be determined, which increases requirements on the readout electronics. Another disadvantage is that optical photons created in the first scintillator need to propagate through the second scintillator in order to be detected. This may cause a dispersion in pulse shape and degrade the timing resolution achievable with this design. The different light output and associated differences in energy resolution of the crystals used in a PSD design may also introduce nonuniformities in scatter rejection capabilities.
It is worth noting that PSD has also been used in the LabPET scanner [31] in order to reduce the number of electronic readout channels. In this design, two crystals with different decay times are positioned next to each other and are coupled to the same photosensor, thus multiplexing the readout by a factor of two.
In order to circumvent the discrete nature of the phoswich approach, Du et al. [32] proposed a continuous phoswich crystal, whereby the far end and part of the sides of a crystal are coated with a phosphor powder. The phosphor re-emits absorbed scintillation light at a later time point and at a lower frequency. Using different pulse shape discrimination and advanced analysis techniques [33], continuous DOI can be obtained. The authors obtained an 8 mm FWHM DOI resolution for a 2-cm-thick array.
28.3.2.2 Crystal Offset Method
A solution to the different response from the different scintillators in a phoswich design is to use a stack of the same scintillator material, albeit with an offset. The offset causes the optical light created in the different layers to follow different paths, resulting in different patterns on the photodetector surface, as shown in Fig. 28.5b. The location of the focal light spot on the photodetector surface thus gives DOI information. Liu et al. [34] stacked a 6 × 6 array of 1.8 × 1.8 × 10 mm3 LSO crystals on top of a 7 × 7 array of the same crystals. The lower array was coupled to a position-sensitive PMT (PS-PMT). Using this approach, the authors observed an improvement from 4.5 mm FWHM to 3.4 mm FWHM at 30° photon incidence, with uniform energy and timing resolution. Zhang et al. [35] stacked a 9 × 9 layer of 2.1 × 2.1 × 6.5 mm3 BGO crystals on top of a 10 × 10 array of 2.1 × 2.1 × 11.5 mm3 BGO crystals, though with moderate crystal identification performance. Ito et al. [36] used a similar approach to stack 4 layers of 29 × 29, 29 × 28, 28 × 28, and 28 × 27 LSO crystals of 1.5 × 1.5 × 7 mm3 each. The second layer was offset by half a pitch in the X direction, the third by half a pitch in the Y direction, and the fourth by an additional half pith in the X direction. Even and odd rows in the flood histogram would thus correspond to even and odd layers. Each individual crystal was wrapped with a reflector. Crystal resolving power in individual layers was excellent, yet the different DOI layers overlapped at the edges of the flood and thus were inseparable, presumably due to loss of photon collection efficiency at the edge. In these designs, the array closest to the photodetector is referred to as the “frontal” layer, and the one further away from the photodetector is the “distal” layer.
While the crystal offset method bypasses some of the disadvantages of the phoswich design, it has its own drawbacks. An offset method will result in nonuniform sensitivity as inevitably the second “distal” layer has less solid angle coverage than the first. A bigger problem is the light collection problem from the distal layer, similar to that of the phoswich design, but worse since light collection for the back crystal elements are split between two front element crystals. In addition, it is often hard to reliable distinguish both layers, in particular for incident photon angles larger than 0°, the angles for which DOI improvement is relevant.
28.3.2.3 Light Sharing Method
In an attempt to improve the nonuniform sensitivity caused by the crystal offset method, various researchers have experimented using different reflector arrangements for different layers, instead of physically offsetting different crystal layers. This method also results in a distinct pattern on the photodetector surface, as shown in Fig. 28.5c. Different reflector configurations are schematically drawn with full and dotted lines in the figure. The crystal location pattern observed on the photodetector is not equidistant in each row, as opposed to the offset design.
Using the light sharing method, Tsuda et al. [37] made a stack of 4 layers of 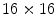 GSO crystals each measuring 1.42 × 1.42 × 4.5 mm3. Each stack contained a different arrangement of light reflectors, so that a different pattern appears on the surface of the photodetector for each individual layer. They were able to achieve separation between the four layers, but with quite significant overlap, leading to layer misidentification.
GSO crystals each measuring 1.42 × 1.42 × 4.5 mm3. Each stack contained a different arrangement of light reflectors, so that a different pattern appears on the surface of the photodetector for each individual layer. They were able to achieve separation between the four layers, but with quite significant overlap, leading to layer misidentification.
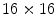 GSO crystals each measuring 1.42 × 1.42 × 4.5 mm3. Each stack contained a different arrangement of light reflectors, so that a different pattern appears on the surface of the photodetector for each individual layer. They were able to achieve separation between the four layers, but with quite significant overlap, leading to layer misidentification.
GSO crystals each measuring 1.42 × 1.42 × 4.5 mm3. Each stack contained a different arrangement of light reflectors, so that a different pattern appears on the surface of the photodetector for each individual layer. They were able to achieve separation between the four layers, but with quite significant overlap, leading to layer misidentification.Inadama et al. [38] used a combination of the light sharing and the phoswich approach to build an 8-layer DOI detector, organized as a 4-layer stack of a phoswich of 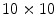 arrays of
arrays of 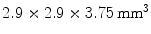 GSO crystals with 0.5 mol% Ce dopant and
GSO crystals with 0.5 mol% Ce dopant and 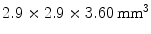 GSO crystals with 1.5 mol% Ce. Each phoswich layer had a different reflector orientation. The authors were able to separate all layers, but also observed large overlap and hence misidentification.
GSO crystals with 1.5 mol% Ce. Each phoswich layer had a different reflector orientation. The authors were able to separate all layers, but also observed large overlap and hence misidentification.
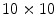 arrays of
arrays of 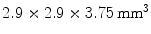 GSO crystals with 0.5 mol% Ce dopant and
GSO crystals with 0.5 mol% Ce dopant and 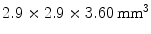 GSO crystals with 1.5 mol% Ce. Each phoswich layer had a different reflector orientation. The authors were able to separate all layers, but also observed large overlap and hence misidentification.
GSO crystals with 1.5 mol% Ce. Each phoswich layer had a different reflector orientation. The authors were able to separate all layers, but also observed large overlap and hence misidentification.28.3.2.4 Dual-Ended Readout
The previously discussed DOI approaches all feature the drawback that the dispersion in the optical photons from the most distal layer will be larger than the dispersion from the proximal crystals, potentially compromising energy and timing resolution of those distal layers. A solution to this problem could be to collect the scintillation light on both sides of the crystal using two photodetectors. Depth information is obtained by the ratio of the signal collected in both photodetectors, as shown in Fig. 28.5d. Dual-ended readout was already proposed in 1988 [39]. These authors placed PMTs in the transaxial direction on both ends of a 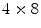 array of
array of 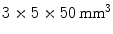 BGO crystals. The setup thus had a radial length of
BGO crystals. The setup thus had a radial length of 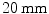 . They were able to obtain a FWHM of 9.5 mm across the 50 mm transaxial direction when irradiating at 0.5 mm intervals.
. They were able to obtain a FWHM of 9.5 mm across the 50 mm transaxial direction when irradiating at 0.5 mm intervals.
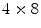 array of
array of 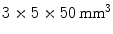 BGO crystals. The setup thus had a radial length of
BGO crystals. The setup thus had a radial length of 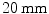 . They were able to obtain a FWHM of 9.5 mm across the 50 mm transaxial direction when irradiating at 0.5 mm intervals.
. They were able to obtain a FWHM of 9.5 mm across the 50 mm transaxial direction when irradiating at 0.5 mm intervals.The development of small silicon-based avalanche photodiodes (APDs) as a replacement for PMTs allowed dual readout in the radial direction. Such an approach was used by the ClearPEM group [40] for use in a dedicated breast PET camera. These researchers coupled two APDs to a 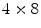 array of
array of 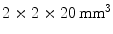 LSO crystals. The introduction of the APD and a thin circuit board between the LSO crystals and the 511-keV source only introduces minimal scatter.
LSO crystals. The introduction of the APD and a thin circuit board between the LSO crystals and the 511-keV source only introduces minimal scatter.
 array of
array of 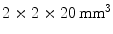 LSO crystals. The introduction of the APD and a thin circuit board between the LSO crystals and the 511-keV source only introduces minimal scatter.
LSO crystals. The introduction of the APD and a thin circuit board between the LSO crystals and the 511-keV source only introduces minimal scatter.James et al. [41] used position-sensitive APDs (PSAPDs) to read out both sides of an array comprising 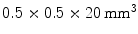 LSO crystals. A DOI resolution of
LSO crystals. A DOI resolution of 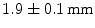 was obtained at a temperature of 0 °C in a design intended to be used for small animal imaging.
was obtained at a temperature of 0 °C in a design intended to be used for small animal imaging.
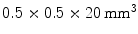 LSO crystals. A DOI resolution of
LSO crystals. A DOI resolution of 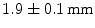 was obtained at a temperature of 0 °C in a design intended to be used for small animal imaging.
was obtained at a temperature of 0 °C in a design intended to be used for small animal imaging.The dual-ended readout seems a promising solution to estimate DOI. However, it comes with a number of drawbacks: the number of photodetectors needs to be doubled and positioning these inside the photon path will introduce additional scatter. Moreover, the continuous approach currently only estimates where the interaction happened, which yields an uncertainty in the DOI coordinate and hence a potentially large misidentification.
28.3.2.5 Direct DOI Measurement
Instead of making an estimate of the interaction location using the ratio of the charge collected at both ends of a scintillation crystal, the AXPET design [42] placed a number of wavelength shifting strip (WLS) underneath an 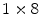 array of
array of 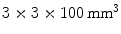 LYSO crystals. The WLS measured
LYSO crystals. The WLS measured 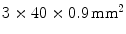 . Both scintillation crystal and WLS are read out by a Si-PM. The authors measured an axial resolution of less than 1.7 mm. A similar approach for a small animal PET camera was used in the COMPET design [43]. The drawback of this approach is the need for photodetectors on four sides of the “block,” and the low light yield of the WLS, potentially reducing the efficiency of the method.
. Both scintillation crystal and WLS are read out by a Si-PM. The authors measured an axial resolution of less than 1.7 mm. A similar approach for a small animal PET camera was used in the COMPET design [43]. The drawback of this approach is the need for photodetectors on four sides of the “block,” and the low light yield of the WLS, potentially reducing the efficiency of the method.
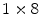 array of
array of 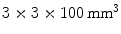 LYSO crystals. The WLS measured
LYSO crystals. The WLS measured 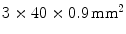 . Both scintillation crystal and WLS are read out by a Si-PM. The authors measured an axial resolution of less than 1.7 mm. A similar approach for a small animal PET camera was used in the COMPET design [43]. The drawback of this approach is the need for photodetectors on four sides of the “block,” and the low light yield of the WLS, potentially reducing the efficiency of the method.
. Both scintillation crystal and WLS are read out by a Si-PM. The authors measured an axial resolution of less than 1.7 mm. A similar approach for a small animal PET camera was used in the COMPET design [43]. The drawback of this approach is the need for photodetectors on four sides of the “block,” and the low light yield of the WLS, potentially reducing the efficiency of the method.In order to obtain direct interaction location measurements in three dimensions, Yamaya et al. [44] built a 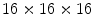 cube of
cube of 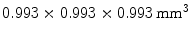 LGSO crystals (X’tal cube). Each of the six faces of the cube was coupled to a
LGSO crystals (X’tal cube). Each of the six faces of the cube was coupled to a 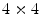 array of Si-PMs. Almost all of the 4,096 crystals were identified in the flood map, albeit with
array of Si-PMs. Almost all of the 4,096 crystals were identified in the flood map, albeit with 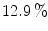 cross talk at the edge and
cross talk at the edge and 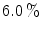 cross talk in the center. The fabrication was improved using a laser to cut microcracks in an LYSO block, resulting in a 3D grid [45]. A
cross talk in the center. The fabrication was improved using a laser to cut microcracks in an LYSO block, resulting in a 3D grid [45]. A 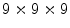 grid with 2 mm pitch was produced using this method. An intrinsic resolution of 2.1 mm was obtained. The design of the X’tal cube is shown in Fig. 28.5e. The obtained flood histogram is actually a 3D histogram.
grid with 2 mm pitch was produced using this method. An intrinsic resolution of 2.1 mm was obtained. The design of the X’tal cube is shown in Fig. 28.5e. The obtained flood histogram is actually a 3D histogram.
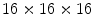 cube of
cube of 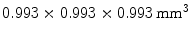 LGSO crystals (X’tal cube). Each of the six faces of the cube was coupled to a
LGSO crystals (X’tal cube). Each of the six faces of the cube was coupled to a 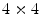 array of Si-PMs. Almost all of the 4,096 crystals were identified in the flood map, albeit with
array of Si-PMs. Almost all of the 4,096 crystals were identified in the flood map, albeit with 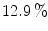 cross talk at the edge and
cross talk at the edge and 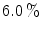 cross talk in the center. The fabrication was improved using a laser to cut microcracks in an LYSO block, resulting in a 3D grid [45]. A
cross talk in the center. The fabrication was improved using a laser to cut microcracks in an LYSO block, resulting in a 3D grid [45]. A 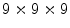 grid with 2 mm pitch was produced using this method. An intrinsic resolution of 2.1 mm was obtained. The design of the X’tal cube is shown in Fig. 28.5e. The obtained flood histogram is actually a 3D histogram.
grid with 2 mm pitch was produced using this method. An intrinsic resolution of 2.1 mm was obtained. The design of the X’tal cube is shown in Fig. 28.5e. The obtained flood histogram is actually a 3D histogram.Another approach for 3D imaging was first proposed conceptually by Levin [46]. In this approach, an array of crystals is coupled to a thin APD. Every layer is directly read out by a photodetector, as shown in Fig. 28.5f. A stack of these detectors forms a 3D block detector. In this particular design, scintillation photons are collected from the sides rather than ends of long scintillation crystal elements, increasing the light yield and removing the dependence of light collection on DOI. Vandenbroucke et al. [47] measured an intrinsic spatial resolution of 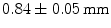 , using an
, using an 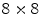 array of
array of 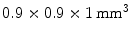 LSO crystals coupled to a PSAPD. The PSAPDs themselves are mounted on a thin Kapton readout circuit in order to decrease the dead area [48]. Because of the small crystals used in this design, and their readout in small cohorts of two
LSO crystals coupled to a PSAPD. The PSAPDs themselves are mounted on a thin Kapton readout circuit in order to decrease the dead area [48]. Because of the small crystals used in this design, and their readout in small cohorts of two 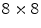 arrays, each individual interaction location of a multiple photon interaction events (MIPE) can be identified. These are events whereby the 511 keV photon Compton scatters once or more than once before it undergoes photoelectric absorption. In order to include these MIPE, the readout electronics need to be carefully designed, so that the trigger threshold can be set as low as possible. A feasibility study of measuring these MIPE events in this stacked design is shown in Ref. [49]. This design is currently incorporated in the construction of a high-resolution breast PET camera [50].
arrays, each individual interaction location of a multiple photon interaction events (MIPE) can be identified. These are events whereby the 511 keV photon Compton scatters once or more than once before it undergoes photoelectric absorption. In order to include these MIPE, the readout electronics need to be carefully designed, so that the trigger threshold can be set as low as possible. A feasibility study of measuring these MIPE events in this stacked design is shown in Ref. [49]. This design is currently incorporated in the construction of a high-resolution breast PET camera [50].
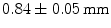 , using an
, using an 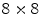 array of
array of 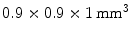 LSO crystals coupled to a PSAPD. The PSAPDs themselves are mounted on a thin Kapton readout circuit in order to decrease the dead area [48]. Because of the small crystals used in this design, and their readout in small cohorts of two
LSO crystals coupled to a PSAPD. The PSAPDs themselves are mounted on a thin Kapton readout circuit in order to decrease the dead area [48]. Because of the small crystals used in this design, and their readout in small cohorts of two 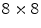 arrays, each individual interaction location of a multiple photon interaction events (MIPE) can be identified. These are events whereby the 511 keV photon Compton scatters once or more than once before it undergoes photoelectric absorption. In order to include these MIPE, the readout electronics need to be carefully designed, so that the trigger threshold can be set as low as possible. A feasibility study of measuring these MIPE events in this stacked design is shown in Ref. [49]. This design is currently incorporated in the construction of a high-resolution breast PET camera [50].
arrays, each individual interaction location of a multiple photon interaction events (MIPE) can be identified. These are events whereby the 511 keV photon Compton scatters once or more than once before it undergoes photoelectric absorption. In order to include these MIPE, the readout electronics need to be carefully designed, so that the trigger threshold can be set as low as possible. A feasibility study of measuring these MIPE events in this stacked design is shown in Ref. [49]. This design is currently incorporated in the construction of a high-resolution breast PET camera [50].Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


