Solutions.


Latin abbreviations are often used to describe the frequency of administration. Some of the commonly used abbreviations are listed in Table 4.1. Sometimes periods are omitted from the abbreviated terms.
TABLE 4.1 Some Latin abbreviations related to dosage frequency
| Latin abbreviation | Meaning |
| ATC | around the clock |
| d. or d | day |
| h. or hr | hour(s) |
| q. | every |
| q. 4h. | every 4 hours |
| q.d | every day |
| b.i.d. | twice a day |
| t.i.d. | three times a day |
| q.i.d. | four times a day (here, “q” does not stand for “every”) |
| h.s. | at bedtime |
| stat | immediately; at once |
As an example, let us consider these directions to the patient:
Sig: 1 tab q 3h [Take one (1) tablet every three (3) hours]
Sig: Chart II h.s. [Take two (2) powders at bedtime]. Notice that in this example the number of doses is given in roman numerals and the number follows the designation for the type of product.
If you need to brush up on Roman numerals go to the next frame. Otherwise, skip to frame 4.

Some values for the Roman symbols of greatest interest to us:
| Roman numeral | Arabic numeral |
| I or i | 1 |
| V or v | 5 |
| X or x | 10 |
| L | 50 |
| C | 100 |
| M | 1000 |
Some rules that apply to Roman numerals:
Examples:
i tab (1 tablet)
caps ii (2 capsules)
VIII gtt (8 drops)
What is meant by “chart III”?

Solution. Three powders in paper.


Solutions.

TABLE 4.2 Selected Latin abbreviations used in the signa
| Latin abbreviation or term | Meaning |
| c. | food; meal(s) |
| a.c. | before meals |
| p.c. | after meals |
 , cum , cum | with |
 , sine , sine | without |
| rep. | repeat |
| p.o., per os | by mouth |
| e.m.p. | in the manner prescribed |
| p.r.n. | as needed, when needed |
An example of a signa is:
Sig: i tab pc  aq [Take one (1) tablet after meals with water.]
aq [Take one (1) tablet after meals with water.]
Translate each of the following signas into clear English.
 2 aspirins q 4h
2 aspirins q 4h aqua; rep. q. 2h.
aqua; rep. q. 2h.
Solutions.
(If these Latin phrases are still Greek to you, review them, try the examples again or try some review problems.)
CALCULATIONS INVOLVING DOSE SIZE, NUMBER OF DOSES, AMOUNT DISPENSED, AND QUANTITY OF AN INGREDIENT
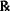 Tetracycline caps Tetracycline caps | 250 mg |
| Disp. caps. No. XII | |
| Sig: 250 mg q.i.d. |
This prescription calls for 12 capsules, each containing 250 mg of tetracycline. If the directions for use were translated literally as “250 mg four (4) times a day,” the patient would not know how many capsules to take. The label should read: “Take one (1) capsule four (4) times a day.”
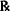 | Penicillin V caps. | 250 mg |
| #24 | ||
| Sig: 250 mg q4h, 1h a.c. |
How would you write the directions to the patient?

Solution. Take one (1) capsule every four (4) hours, one (1) hour before meals.

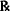 | Sulfisoxazole tabs | 0.5 g |
| Dispense #XLIV | ||
| Sig: 2.0 g stat, 1.0 g t.i.d. |

Solutions.


Solutions.

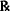 | Sulfadiazine tablets 0.5 |
| d.t.d. No. L | |
| Sig: Tabs II p.c. and h.s. |

Solution. About 6 days
CALCULATION
Assuming that the patient eats 3 meals a day, he will take 8 tablets each day. Thus
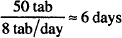

 Aspirin Aspirin | 300 mg |
| Phenylpropanolamine hydrochloride | 20 mg |
| Lactose qs ad | 600 mg |
| d.t.d. caps #XXIV | |
| Sig: II q 4h |
This prescription is for an adult.
The usual dose of phenylpropanolamine hydrochloride is listed as “25 to 50 mg every 3 or 4 hours.”
Calculate the dose of phenylpropanolamine hydrochloride in the prescription and compare it with the usual dose.

Solution. Each capsule contains 20 mg of phenylpropanolamine hydrochloride. The patient is therefore taking 40 mg of this drug every 4 hours, which appears to be a satisfactory dose.

 Ephedrine sulfate Ephedrine sulfate | 0.48 |
| Aspirin | 7.2 |
| Caffeine | 0.24 |
| Div. in caps #XXIV | |
| Sig: Caps II q. 6h. p.r.n. |
How much ephedrine sulfate will the patient be given in each dose, which consists of two capsules?

Solution. 40 mg
CALCULATION
The quantity of ephedrine sulfate in each capsule may be found by dividing the total quantity of this material by the number of capsules:
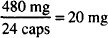
Thus two capsules will contain 40 mg.

 Hydrocortisone Hydrocortisone | 0.6 g | |
| Sodium salicylate | 30.0 g | |
| Div. in caps #LX | ||
| Sig: caps I q 8 h. |

Solution. 30 mg per day. (Each capsule contains 10 mg; 3 capsules are taken each day.)

The dosage of bulk liquids is usually given in terms of household measuring devices such as the teaspoon or tablespoon. There are no uniform, official standards to which household teaspoons are made, and a teaspoon found at home may be daintier or heftier than average. According to the official compendia, the average teaspoon holds about 5 mL, but teaspoons in use may contain 4.93 ± 0.24 mL.
In all of our calculations, we will assume that the capacities listed in Table 4.3 are correct. However, to ensure that the patient is actually receiving the intended volume, the pharmacist should give the patient an accurately calibrated measuring device each time a liquid medication is dispensed.
TABLE 4.3 Household devices used to measure liquid medication
| Household measure | Nominal capacity (ml.) |
| 1 teaspoonful (tsp) | 5 |
| 1 tablespoonful (1/2 fξ) (tbsp) | 15 |
| 1 glassful (8 fξ) | 240 |
If a 10-mL dose is required, the patient should be directed to take 2 teaspoonfuls. Note that a fluidounce contains 2 tablespoonfuls or 6 teaspoonfuls.
Learn the table. Then fill in the blanks:

Solutions.

 aqua p.c.
aqua p.c.
Solutions.

Tsp ii stat
Tsp i b.i.d. d 2 et 3
Tsp ii p.m. d 4 and thereafter.

Solution. 300 mL
CALCULATIONS
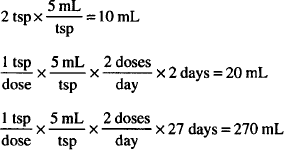
Total to be dispensed = 10 + 20 + 270 = 300 mL

 | Tetracycline oral syrup |
Sig: tsp   q.i.d. for 6 days q.i.d. for 6 days |
How many milliliters of tetracycline oral syrup should be dispensed?

Solution. 60 mL
CALCULATIONS
The directions state: “One-half (1/2) teaspoonful four (4) times a day for six (6) days.” The patient will therefore take


 | Potassium bromide | 5.4 g |
| Aqua | 30.0 mL | |
| Cherry syrup | qs ad 120.0 mL | |
| Sig: 1 tsp qid |

Solution. 0.9 g
CALCULATIONS
A total of 4 teaspoonfuls, or 20 mL, of the syrup will be taken each day. The amount of potassium bromide in that quantity can be calculated in several ways. One approach is to set up a proportion, recognizing that the relative content of potassium bromide is the same in any volume of the syrup.
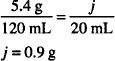

1 tsp tid
How many days will this medication last the patient?

Solutions. 6 days
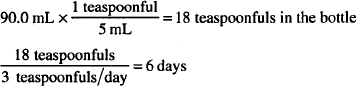

 | Chlorpheniramine maleate syrup | 2 mg/5 mL |
| Disp 3-day supply | ||
| Sig: 4 mg b.i.d. |
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


