10
Calculations involving molecular weights
Many pharmaceutical calculations involve the need to know the molecular weight or molecular structure of the drug. In some cases these can be found in reference books, but on some occasions it may be necessary to work out the molecular weight from the individual atomic weights.
Calculations involving molecular weights are rarely seen in community pharmacy. They are, however, more usual in hospital pharmacy. A common situation when these calculations are used is when a patient has presented with an electrolyte imbalance. Since the electrolyte imbalance will be specific to each patient, a standard intravenous infusion may need to have amounts of various ions, such as potassium, added. Often the amount to be added will be calculated using the molecular weight of the available product.
Molecular weights of drugs
The molecular weight of a drug is the sum of all the atomic weights of the individual atoms in the molecule expressed in grams. For example, a molecule of potassium bromide (KBr) consists of one atom of potassium and one atom of bromine (atomic weights are given in Appendix 4), so the molecular weight of potassium bromide is:
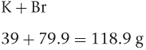
If there is more than one atom of the same kind in a molecule, all the individual atoms must be included in the calculation. For example, aluminium chloride (AlCl3) consists of one atom of aluminium and three atoms of chlorine, so the molecular weight of aluminium chloride is:
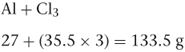
If a molecule has associated water molecules, these must be included in the calculation of molecular weight. For example, the molecular weight of zinc sulfate monohydrate (ZnSO4.H2O) is:
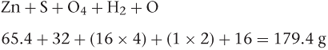
The formulae of the above molecules are simple. Many drug molecules have much more complicated formulae and to calculate the molecular weight it is easier to use the empirical formula than the structural formula. For example, the empirical formula of aspirin is C9H8O4, so the molecular weight can be calculated as follows:
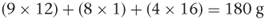
The structural formula of aspirin is:
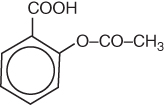
From the structural formula it is not readily clear how many atoms of each element are present. In order to calculate the molecular weight from the structural formula, it is therefore necessary to determine the number of each atom in the empirical formula. However, during the process of converting the structural formula into the empirical formula, it is easy to introduce errors; therefore, wherever possible, if the empirical formula is available it should be used. Empirical and structural formulae of drugs can be found in official publications, e.g. The Pharmaceutical Codex, Martindale and pharmacopoeias.
Knowledge of the molecular weight of a compound or drug allows the calculation of the amount of element/base/salt present in that compound or drug. With some drugs, it is only one part of the molecule that is pharmacologically active.
Some pharmaceutical calculations require the percentage of a specific component of a drug to be determined. In such cases it may be necessary to use a knowledge of molecular weights.
Drugs and their salts
Some drugs may be prepared with different salts attached to the basic drug molecule. For example, iron is presented as a number of different ferrous salts. The ferrous salts that are available for use as drugs are fumarate, gluconate, succinate, sulfate and dried sulfate. Although different salts of a drug may be prescribed, it is normal to give an equivalent amount of the base drug. It such a case it may be necessary to calculate the equivalent amount of base drug in two different salts.
Equivalent amounts of drug in different salts of that drug
In Example 10.3 two salts of iron are compared in terms of their iron content.
Calculating the weight of the salt, if the drug is expressed as the base
Many drug preparations consist of the salt (or salts) of a base drug. However, in describing the drug preparation it is usual to express the dose or strength in terms of the base drug rather than the actual salt used in the preparation. One such example is the drug erythromycin. Some of the available formulations of erythromycin are as follows:
- Erythrocin tablets contain 250 mg and 500 mg erythromycin (as stearate).
- The paediatric suspension contains 125 mg, 250 mg and 500 mg of erythromycin (as the ethyl succinate) per 5 mL.
- The intravenous infusion powder is presented as a vial containing 1 g erythromycin (as lactobionate).
- The paediatric suspension contains 125 mg, 250 mg and 500 mg of erythromycin (as the ethyl succinate) per 5 mL.
In other words, the paediatric suspensions contain an amount of erythromycin ethyl succinate that is equivalent to 125 mg, 250 mg and 500 mg of erythromycin in every 5 mL. The 250-mg and 500-mg erythrocin tablets contain, respectively, the equivalent of 250 mg and 500 mg of erythromycin presented as the stearate.
If the empirical formulae of erythromycin, erythromycin ethyl succinate and erythromycin stearate are known, it is possible to calculate the amount of the erythromycin salt required in each preparation, i.e. to give a known quantity of erythromycin.
The molecular weights are:
| erythromycin | 734 |
| erythromycin ethyl succinate | 862 |
| erythromycin stearate | 1018 |
Using the same approach the amount of adrenaline acid tartrate in adrenaline injection can be determined.
Calculations in which the base to salt ratio is more than 1
When some drug bases are converted into a salt the resultant molecule may consist of two or more base units attached to one salt unit. For example, salbutamol has the empirical formula C13H21NO3 and salbutamol sulfate has the formula (C13H21NO3)2.H2SO4. It can be seen that one molecule of salbutamol sulfate contains two molecules of the base and this must be taken into account in calculations as shown in the next example.
Using weights of salts expressed as equivalent to a known weight of base
In some official publications the salts of a drug are expressed as an amount equivalent to a known amount of the anhydrous base. For example, the British National Formulary (BNF) notes that ‘quinine (anhydrous base) 100 mg is equivalent to quinine bisulfate 169 mg is equivalent to quinine dihydrochloride 122 mg is equivalent to 121 mg of quinine sulfate’.
The equivalent values for the quinine salts can be used to determine the approximate amount of quinine anhydrous base in a tablet containing a quinine salt.



