On the basis of the observed genotype frequencies, we can directly determine the allele frequencies by simply counting the alleles. In this context, when we refer to the population frequency of an allele, we are considering a hypothetical gene pool as a collection of all the alleles at a particular locus for the entire population. For autosomal loci, the size of the gene pool at one locus is twice the number of individuals in the population because each autosomal genotype consists of two alleles; that is, a ΔCCR5/ΔCCR5 individual has two ΔCCR5 alleles, and a CCR5/ΔCCR5 individual has one of each. In this example, then, the observed frequency of the CCR5 allele is:
(2×647)+(1×134)788×2=0.906
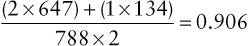
Similarly, one can calculate the frequency of the ΔCCR5 allele as 0.094, by adding up how many ΔCCR5 alleles are present [(2 × 7) + (1 × 134)] = 148 out of a total of 1576 alleles in this sample], resulting in a ΔCCR5 allele frequency of 148/1576 = 0.094. Alternatively (and more simply), one can subtract the frequency of the normal CCR5 allele, 0.906, from 1, because the frequencies of the two alleles must add up to 1, resulting in a ΔCCR5 allele frequency of 0.094.
The Hardy-Weinberg Law
As we have just shown with the CCR5 example, we can use a sample of individuals with known genotypes in a population to derive estimates of the allele frequencies by simply counting the alleles in individuals with each genotype. How about the converse? Can we calculate the proportion of the population with various genotypes once we know the allele frequencies? Deriving genotype frequencies from allele frequencies is not as straightforward as counting because we actually do not know in advance how the alleles are distributed among homozygotes and heterozygotes. If a population meets certain assumptions (see later), however, there is a simple mathematical equation for calculating genotype frequencies from allele frequencies. This equation is known as the Hardy-Weinberg law. This law, the cornerstone of population genetics, was named for Godfrey Hardy, an English mathematician, and Wilhelm Weinberg, a German physician, who independently formulated it in 1908.
The Hardy-Weinberg law has two critical components. The first is that under certain ideal conditions (see Box), a simple relationship exists between allele frequencies and genotype frequencies in a population. Suppose p is the frequency of allele A, and q is the frequency of allele a in the gene pool. Assume alleles combine into genotypes randomly; that is, mating in the population is completely at random with respect to the genotypes at this locus. The chance that two A alleles will pair up to give the AA genotype is then p2; the chance that two a alleles will come together to give the aa genotype is q2; and the chance of having one A and one a pair, resulting in the Aa genotype, is 2pq (the factor 2 comes from the fact that the A allele could be inherited from the mother and the a allele from the father, or vice versa). The Hardy-Weinberg law states that the frequency of the three genotypes AA, Aa, and aa is given by the terms of the binomial expansion of (p + q)2 = p2 + 2pq + q2. This law applies to all autosomal loci and to the X chromosome in females, but not to X-linked loci in males who have only a single X chromosome.
The Hardy-Weinberg Law
The Hardy-Weinberg law rests on these assumptions:
• The population under study is large, and matings are random with respect to the locus in question.
• Allele frequencies remain constant over time because of the following:
• There is no appreciable rate of new mutation.
• Individuals with all genotypes are equally capable of mating and passing on their genes; that is, there is no selection against any particular genotype.
• There has been no significant immigration of individuals from a population with allele frequencies very different from the endogenous population.
A population that reasonably appears to meet these assumptions is considered to be in Hardy-Weinberg equilibrium.
The law can be adapted for genes with more than two alleles. For example, if a locus has three alleles, with frequencies p, q, and r, the genotypic distribution can be determined from (p + q + r)2. In general terms, the genotype frequencies for any known number of alleles an with allele frequencies p1, p2, … pn can be derived from the terms of the expansion of (p1 + p2 + … pn)2.
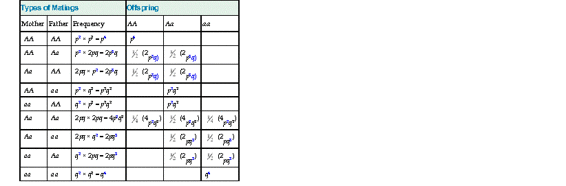
A second component of the Hardy-Weinberg law is that if allele frequencies do not change from generation to generation, the proportion of the genotypes will not change either; that is, the population genotype frequencies from generation to generation will remain constant, at equilibrium, if the allele frequencies p and q remain constant. More specifically, when there is random mating in a population that is at equilibrium and genotypes AA, Aa, and aa are present in the proportions p2 : 2pq : q2, then genotype frequencies in the next generation will remain in the same relative proportions, p2 : 2pq : q2. Proof of this equilibrium is shown in Table 9-2. It is important to note that Hardy-Weinberg equilibrium does not specify any particular values for p and q; whatever allele frequencies happen to be present in the population will result in genotype frequencies of p2 : 2pq : q2, and these relative genotype frequencies will remain constant from generation to generation as long as the allele frequencies remain constant and the other conditions introduced in the Box are met.
TABLE 9-2
Frequencies of Mating Types and Offspring for a Population in Hardy-Weinberg Equilibrium with Parental Genotypes in the Proportion p2 : 2pq : q2
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


