and Jordan Smoller2
(1)
Department of Epidemiology, Albert Einstein College of Medicine, Bronx, NY, USA
(2)
Department of Psychiatry and Center for Human Genetic Research, Massachusetts General Hospital, Boston, MA, USA
The theory of probability is at bottom nothing but common sense reduced to calculus.
Pierre Simon De Le Place
Theori Analytique des Probabilites (1812–1820)
2.1 What Is Probability?
The probability of the occurrence of an event is indicated by a number ranging from 0 to 1. An event whose probability of occurrence is 0 is certain not to occur, whereas an event whose probability is 1 is certain to occur.
The classical definition of probability is as follows: if an event can occur in N mutually exclusive, equally likely ways and if n A of these outcomes have attribute A, then the probability of A, written as P(A), equals n A /N. This is an a priori definition of probability, that is, one determines the probability of an event before it has happened. Assume one were to toss a die and wanted to know the probability of obtaining a number divisible by three on the toss of a die. There are six possible ways that the die can land. Of these, there are two ways in which the number on the face of the die is divisible by three, a 3 and a 6. Thus, the probability of obtaining a number divisible by three on the toss of a die is 2/6 or 1/3.
In many cases, however, we are not able to enumerate all the possible ways in which an event can occur, and, therefore, we use the relative frequency definition of probability. This is defined as the number of times that the event of interest has occurred divided by the total number of trials (or opportunities for the event to occur). Since it is based on previous data, it is called the a posteriori definition of probability.
For instance, if you select at random a white American female, the probability of her dying of heart disease is 0.00199. This is based on the finding that per 100,000 white American females, 199 died of coronary heart disease (estimates are for 2011, National Vital Statistics System, National Center for Health Statistics, Centers for Disease Control and Prevention). When you consider the probability of a white American female who is between ages 45 and 54, the figure drops to 0.00041 (or 41 women in that age group out of 100,000), and when you consider women 75–84 years old, the figure rises to 0.00913 (or 913 per 100,000). For white men 75–84 years old, it is 0.01434 (or 1,434 per 100,000). The two important points are (1) to determine a probability, you must specify the population to which you refer, for example, all white females, white males between 65 and 74, nonwhite females between 65 and 74, and so on; and (2) the probability figures are constantly revised as new data become available.
This brings us to the notion of expected frequency. If the probability of an event is P and there are N trials (or opportunities for the event to occur), then we can expect that the event will occur N × P times. It is necessary to remember that probability “works” for large numbers. When in tossing a coin we say the probability of it landing on heads is 0.50, we mean that in many tosses half the time the coin will land heads. If we toss the coin ten times, we may get three heads (30 %) or six heads (60 %), which are a considerable departure from the 50 % we expect. But if we toss the coin 200,000 times, we are very likely to be close to getting exactly 100,000 heads or 50 %.
Expected frequency is really the way in which probability “works.” It is difficult to conceptualize applying probability to an individual. For example, when TV announcers proclaim there will be, say, 400 fatal accidents in State X on the Fourth of July, it is impossible to say whether any individual person will in fact have such an accident, but we can be pretty certain that the number of such accidents will be very close to the predicted 400 (based on probabilities derived from previous Fourth of July statistics).
2.2 Combining Probabilities
There are two laws for combining probabilities that are important. First, if there are mutually exclusive events (i.e., if one occurs, the other cannot), the probability of either one or the other occurring is the sum of their individual probabilities. Symbolically,
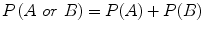
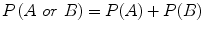
An example of this is as follows: the probability of getting either a 3 or a 4 on the toss of a die is 1/6 + 1/6 = 2/6.
A useful thing to know is that the sum of the individual probabilities of all possible mutually exclusive events must equal 1. For example, if A is the event of winning a lottery, and not A (written as 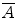 ), is the event of not winning the lottery, then
), is the event of not winning the lottery, then 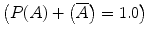 and
and 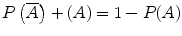 .
.
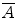 ), is the event of not winning the lottery, then
), is the event of not winning the lottery, then 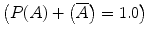 and
and 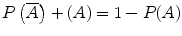 .
. Second, if there are two independent events (i.e., the occurrence of one is not related to the occurrence of the other), the joint probability of their occurring together (jointly) is the product of the individual probabilities. Symbolically,
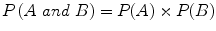
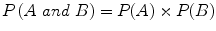
An example of this is the probability that on the toss of a die you will get a number that is both even and divisible by 3. This probability is equal to 1/2 × 1/3 = 1/6. (The only number both even and divisible by 3 is the number 6.)
The joint probability law is used to test whether events are independent. If they are independent, the product of their individual probabilities should equal the joint probability. If it does not, they are not independent. It is the basis of the chi-square test of significance, which we will consider in the next section.
Let us apply these concepts to a medical example. The mortality rate for those with a heart attack in a special coronary care unit in a certain hospital is 15 %. Thus, the probability that a patient with a heart attack admitted to this coronary care unit will die is 0.15 and that he will survive is 0.85. If two men are admitted to the coronary care unit on a particular day, let A be the event that the first man dies and let B be the event that the second man dies.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


