OUTLINE
Freezing Point Depression Method
Sodium Chloride Equivalent Method
I. GENERAL PRINCIPLES
A. Pharmaceutical solutions are sometimes applied to the sensitive membranes of the eye or nasal passages, or they may be injected into muscles, blood vessels, organs, tissue, or lesions. These solutions should be adjusted to have approximately the same osmotic pressure as that of body fluids because solutions that have the same osmotic pressure as cell contents do not cause a net movement of fluid into or out of the cells and therefore do not cause tissue damage or discomfort when placed in contact with cells. Solutions that exert the same osmotic pressure are called isoosmotic; solutions that exert the same osmotic pressure as a body fluid are termed isotonic, meaning of equal tone.
B. Osmotic pressure, like vapor pressure lowering, freezing point depression, and boiling point elevation, is a colligative property. Colligative properties depend not on the weight or the nature of the solute present in solution but only on the number of solute particles per given volume of solution. For example, one mole of dextrose (180 grams), when dissolved in one liter of solution, has the same effect on the osmotic pressure as does one mole per liter of sucrose (342 grams). Both of these substances are nonelectrolytes, and one mole of each gives an equal number of solute particles (Avogadro’s number—6.02 × 1023) when dissolved in water. In contrast, one mole of a univalent–univalent electrolyte, such as sodium chloride (58.5 grams), has twice the effect on osmotic pressure when dissolved in a liter of water because each sodium chloride gives two particles, an Na+ ion and a Cl− ion, when this salt is dissolved in water.
C. For pharmaceutical solutions, though we are interested in the changes in osmotic pressure caused by dissolved drugs and chemicals, we usually measure changes in freezing point caused by these substances. This is because osmotic pressure is difficult to measure directly, whereas freezing points are determined rather easily. Because both osmotic pressure and freezing point depression are colligative properties, freezing point depression can be used as a measure of change in osmotic pressure caused by dissolved drug or solute.
D. The fundamental expression relating freezing point depression and concentration of solute in solution is given by the equation
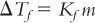
where ΔTf is the freezing point depression, Kf is the molal depression constant, and m is the molal concentration of the solute in solution. For water, which has a normal freezing point of 0°C at normal atmospheric pressure of 1 atm, Kf is 1.86, and the freezing point depression, ΔTf, for a 1 m aqueous solution is 1.86°C.
E. The foregoing equation and the molal depression constant hold true only for nonelectrolytes in dilute solution. Though the freezing point depression of a 1-molal solution of a nonelectrolyte is approximately 1.86°C, electrolytes give larger molal freezing point depressions, the amount dependent on the number of ions generated per molecule, the degree of dissociation, and the degree of attraction of ions for the solvent. If a univalent–univalent solute such as sodium chloride were completely dissociated in water and if the molecules behaved ideally, a 1-molal aqueous solution of sodium chloride would have a freezing point of 2 × −1.86° = −3.72°C. Because molecules do not behave ideally in solution, the actual freezing point depression is somewhat less, and the measured freezing point is approximately −3.35°C. (This discrepancy is an experimental measure of the extent of nonideal behavior.) The van’t Hoff equation takes these factors into account with the equation
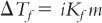
where i, the van’t Hoff factor, is the ratio of the colligative effect produced by a given concentration of electrolyte divided by the effect observed for the same concentration of nonelectrolyte.
F. This expression has been further modified for the dilute aqueous solutions encountered at isotonic concentrations to give the useful equation:
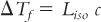
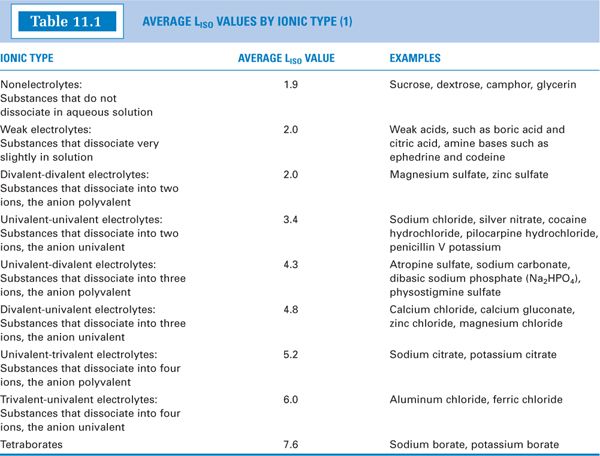
where c is the molar (rather than the molal) concentration of solute in aqueous solution and Liso is the experimentally determined iKf, the molar freezing point depression at isotonic concentration of the various ionic types (e.g., nonelectrolytes, univalent-univalent electrolytes, univalent-divalent electrolytes). Table 11.1 gives average Liso values for various ionic types (1). The foregoing equation and the values in Table 11.1 can be used to estimate freezing point depression for solutes in aqueous solution for which there are no published values of freezing point depression for that solute.
G. Known concentrations of various drugs and chemicals have been dissolved in water and the freezing points of the solutions measured. These values have been published, and the table in Appendix D gives values for many common drugs; more complete tables of values can be found in Remington:The Science and Practice of Pharmacy, and in the miscellaneous tables section in the back of the 13th edition of The Merck Index. For more information on this subject, consult a book on physical pharmacy such as Martin’s Physical Pharmacy and Pharmaceutical Sciences or the applicable chapters in Remington:The Science and Practice of Pharmacy.
II. FREEZING POINT DEPRESSION METHOD
A. Scientists have accurately measured the freezing points of the two critical body fluids, blood and tears, and have found these to be approximately the same: −0.52°C. For drug solutions to be isotonic with these fluids, they must have this same freezing point.
B. As stated, the freezing point depressions of many drugs in various concentrations in water have been measured and published in tables such as those shown in Appendix D, where the values in the column marked ΔTf1% are the freezing point depressions in degrees Celsius of 1% solutions of the drug or chemical in water. Because freezing point depression is additive, pharmacists can use these data to calculate the amount of solute to add in making isotonic solutions (i.e., in making solutions with the same freezing point as blood or tears). This method of adjusting the tonicity of solutions using freezing point depression is shown next. The values for the example are taken from Appendix D.

C. Basic steps of the freezing point depression method
1. Note or determine the percent concentration of the drug in the prescribed solution.
2. Read from Appendix D the freezing point depression caused by a 1% concentration of the drug in solution.
3. Calculate the freezing point depression caused by the prescribed concentration of drug in solution.
4. Subtract this from the desired freezing point depression of 0.52°.
5. Decide on an appropriate solute for adjusting the tonicity of the solution.
6. Using the table, determine the freezing point depression caused by a 1% concentration of this solute in solution.
7. Calculate the concentration of this solute needed to give the remaining freezing point depression.
8. Calculate the weight of solute in grams needed for the desired quantity of solution.

1. Note or determine the percent concentration of the drug in the prescribed solution: 2%.
2. Read from Appendix D the freezing point depression caused by a 1% concentration of the drug in solution: 0.07°.
3. Calculate the freezing point depression caused by the prescribed concentration of drug in solution.
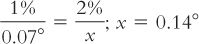
4. Subtract this from the desired freezing point depression of 0.52°.
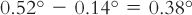
5. Decide on an appropriate solute for adjusting the tonicity of the solution: boric acid.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree