Tetracycline hydrochloride
5.0 g
Methyl parahydroxybenzoate
0.1 g
Sodium citrate
6.5 g
Sorbitol, liquid (crystallising)
65.5 g
Tragacanth
0.5 g
Water, purified
40.0 g
Total
118.2 g (= 100 mL)
Chloramphenicol has an extremely bitter taste. When this antibiotic is used orally, it should be formulated as a suspension, using the insoluble chloramphenicol palmitate.
In the European Pharmacopoeia (Ph. Eur.) various definitions for solubilities in water are described, i.e. from “very soluble” to “practically insoluble” (Table 18.2) [1]. The solubility is also indicated by the amount of water, in millilitres, necessary to dissolve 1 g of the substance at room temperature. The solubility of a substance can also be specified in grams per Litre.
Table 18.2
Explanation of the Definitions for the Solubility in Water as specified in the Ph. Eur.
Solubilitya | |
|---|---|
Very soluble | Less than 1 |
Freely soluble | From 1 to 10 |
Soluble | From 10 to 30 |
Sparingly soluble | From 30 to 100 |
Slightly soluble | From 100 to 1,000 |
Very slightly soluble | From 1,000 to 10,000 |
Practically insoluble | More than 10,000 |
Although the terms in Table 18.2 to describe the solubility of an active substance are still used in many handbooks, from a clinical view they are no longer used. The principle of solubility in perspective is now used. That is, the solubility of an active substance is connected to the dose that should be administered to the patient. Thus, solubility in perspective is not a pure physico-chemical characteristic of the active substance. For example, the solubility will not cause any problems when an active substance with a low solubility has to be given to a patient as a solution at a very low concentration. In Chap. 17 Product design and in Chap. 16 Biopharmaceutics this concept will be explained in more detail.
The rate at which an active substance dissolves does not only depend on the solubility of the active substance. The dissolution of an active substance is described by the Noyes-Whitney equation:
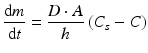
where dm/dt is the dissolution rate, D the diffusion coefficient of the active substance in solution, A the contact surface area of the active substance with the solvent, h the thickness of the diffusion layer, Cs the solubility of the active substance and C the concentration of the active substance in the bulk of the solution.
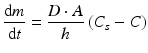
(18.1)
Amongst other strategies, the solubility of a substance can be influenced by variation of the pH, salt formation, variation of the solvent, complex formation, or derivatisation. These concepts, with pharmaceutical preparations as examples, are explained below.
18.1.1 Solubility and pH
Most substances are more easily dissolved in water when they are ionised. The degree of ionisation for many substances depends on the pH. Many active substances are weak acids or weak bases. The degree of ionisation, and thus the solubility, can be influenced by adjusting the pH of the medium. The solubility of a non-ionised weak acid can be increased by raising the pH, while the solubility of a non-ionised weak base can be increased by lowering the pH.
The pKa value of an acid indicates how weak the acid is: the higher the pKa value, the weaker the acid. Thus when a weak acid is dissolved in pure water, the decrease of the pH and the extent of dissociation of the acid will be less when the pKa value increases. The relationship of the pH, pKa, and the concentrations of a non-ionised acid [HA] and its salt [A-] is given by the Henderson-Hasselbalch equation:
![$$ \mathrm{p}\mathrm{H}=\mathrm{p}{\mathrm{K}}_{\mathrm{a}}+ \log \frac{\left[{A}^{-}\right]}{\left[HA\right]} $$](/wp-content/uploads/2017/01/A315000_1_En_18_Chapter_Equ2-1.gif)
When the pKa of a substance is known, the fraction ionised active substance as a function of the pH can be calculated using the following derivatives of this equation:
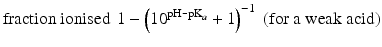
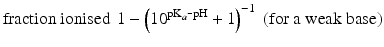
The pKa of phenobarbital is 7.4. When the pH is adjusted to 5.4, 7.4 or 9.4, the fraction ionised active substance will be: 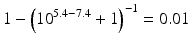 ;
; 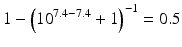 or
or 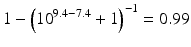 , respectively. This example emphasises that by varying the pH around the pKa, the fraction of ionised active substance can be strongly affected: up to 2 pH units below the pKa, only 1 % is ionised, whereas at 2 pH units above the pKa 99 % is ionised.
, respectively. This example emphasises that by varying the pH around the pKa, the fraction of ionised active substance can be strongly affected: up to 2 pH units below the pKa, only 1 % is ionised, whereas at 2 pH units above the pKa 99 % is ionised.
![$$ \mathrm{p}\mathrm{H}=\mathrm{p}{\mathrm{K}}_{\mathrm{a}}+ \log \frac{\left[{A}^{-}\right]}{\left[HA\right]} $$](/wp-content/uploads/2017/01/A315000_1_En_18_Chapter_Equ2-1.gif)
(18.2)
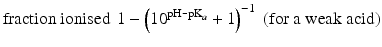
(18.3)
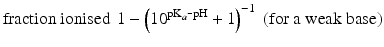
(18.4)
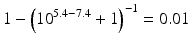 ;
; 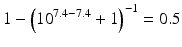 or
or 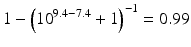 , respectively. This example emphasises that by varying the pH around the pKa, the fraction of ionised active substance can be strongly affected: up to 2 pH units below the pKa, only 1 % is ionised, whereas at 2 pH units above the pKa 99 % is ionised.
, respectively. This example emphasises that by varying the pH around the pKa, the fraction of ionised active substance can be strongly affected: up to 2 pH units below the pKa, only 1 % is ionised, whereas at 2 pH units above the pKa 99 % is ionised.For a further understanding of the dissolution of a substance by salt formation, some basic concepts of analytical chemistry are summarised (Fig. 18.1).
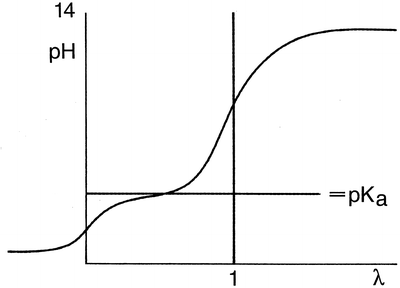

Fig. 18.1
Titration of a weak monovalent acid with a strong base
When an aqueous solution of a weak monovalent acid in water is titrated with NaOH, the pH strongly increases with the first amounts of added NaOH, but when the pH almost reaches the proteolytic constant or the pKa value of the acid, the pH changes to a lesser extent. When the pH is one to two units above the pKa, the pH again rises sharply upon adding more NaOH. For a titration, the amount of added reagent (in this case NaOH) divided by the quantity of the substance to be determined (both in moles) has been defined as λ. The pH of the initially acidic solution (λ = 0) is dependent on the concentration and the degree of dissociation of the acid. When the pH is around the pKa, the solutions acts as a buffer because the addition of a small amount of acid or base will hardly affect the pH. When λ = 0.5, the pH equal to the pKa, there is an equal amount of acid and salt present. In this situation, the buffer capacity is maximal. The equivalence point of the titration is found when λ = 1.
A salt composed of a weak base and a strong acid lowers the pH in aqueous solution. Conversely, a salt composed of a weak acid and a strong base raises the pH in aqueous solution. Examples are lidocaine hydrochloride (acid reaction) and sodium phenobarbital (alkaline reaction), respectively. When the pH of aqueous solutions of these substances is adjusted to pH = 7, lidocaine and phenobarbital, respectively, are partially formed again and precipitate.
The so-called pHp equations (18.5 and 18.6) can be used to calculate the solubility of a weak acid or a weak base as a function of the pH [2, 5]. pHp is an abbreviation for pH precipitation, the pH at which just no precipitation occurs. At a given concentration, the weak acid will precipitate when the pH is lower than the pHp and the weak base will precipitate when the pH is higher than the pHp.
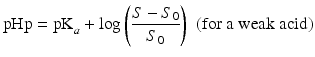
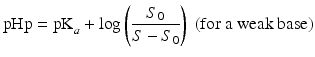
where S0 is the solubility of the undissociated acid or base and S the concentration of the acid or base which has been added initially (both in mole/L).
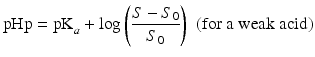
(18.5)
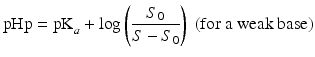
(18.6)
The pHp equation can be illustrated in more detail with an example of a calculation. Suppose a 1 % w/v solution of sodium phenobarbital should be prepared. The following information can be obtained from the Merck Index [6]:
MW phenobarbital = 232.32 g/mol;
MW sodium phenobarbital = 254.22 g/mol;
Solubility phenobarbital in water = 1 g/L;
pKa (phenobarbital) = 7.4.
It follows:
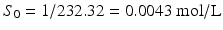 ;
;
1 % w/v corresponds to 10 g/L; thus:
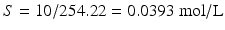 ;
;
Thus the pHp becomes:
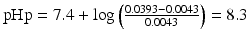 .
.
It follows that in order to obtain a 1 % w/v sodium phenobarbital solution, the pH must be at least 8.3. At a pH lower than 8.3, phenobarbital will remain partially undissolved.
However, the choice of pH cannot be unlimited. In particular at a high or a low pH, the active substance can for example be chemically unstable. In addition, an extreme pH can be incompatible with other components in the solution, for example, preservatives. In addition, the selected pH should also be compatible with the route of administration.
Thus with the correct setting of the pH, either a solution or a suspension can be obtained. The preparation of solutions and suspensions by manipulation of the pH will be illustrated with a number of examples.
There are several ways to adjust the pH to a certain value, which are essentially not different. Either NaOH or HCl can be added to obtain a suitable pH at which the salt is soluble, or the pHp equation can be used to calculate the amount of an acid or a base with its corresponding salt that will be soluble.
Examples of pharmaceutical preparations in which the active substance is dissolved by influencing the pH are infusion or inhalation solutions with acetylcysteine and a furosemide oral solution (Table 18.3). In both cases, a weak acid is brought into solution by raising the pH. Usually sodium hydroxide is used for acetylcysteine and in the formulation of Table 18.3 the primary amine trometamol is used for furosemide.
Furosemide | 0.2 g |
Methyl parahydroxybenzoate | 0.075 g |
Propyl parahydroxybenzoate | 0.025 g |
Saccharin sodium | 0.1 g |
Trometamol | 0.1 g |
Water, purified | ad 100 mL |
Tetracycline hydrochloride easily dissolves in water, to give an acidic solution. In Tetracycline hydrochloride cream 3 % FNA, the pH is adjusted to about 5.5 by adding sodium citrate to a tetracycline hydrochloride solution (Table 18.4). At this pH, tetracycline is insoluble and therefore a suspension is formed. In undissolved state tetracycline is chemically more stable than in the dissolved state. Moreover, a pH of 5.5 is only slightly lower than the third proteolytic constant of citrate (pKa = 6.4 at 25 °C), so a citrate buffer is formed. This saves tetracycline from dissolving again due to slight pH decrease.
Tetracycline hydrochloride | 3 g |
Sodium citrate | 4 g |
Water, purified | 11 g |
Cetomacrogol cream FNAa | 82 g |
Total | 100 g |
Tetracycline is an amphoteric substance which forms salts in both an acidic and an alkaline environment. The substance dissolves at a pH higher than about 8. This was made use of in the preparation of a solution of tetracycline for eye drops (Table 18.5). By the addition of borax, a pH of about 8.2 is reached. As a consequence, tetracycline readily dissolves.
Tetracycline hydrochloride | 0.5 g |
Borax | 0.5 g |
Sodium chloride | 0.7 g |
Water, purified | ad 100 mL |
Is a bumetanide infusion solution 5 mg in 50 mL (syringe for a pump) possible as a solution? The pH of the licensed product (injection solution 0.5 mg/mL) is 7.0. According to information from the manufacturer, the concentration should be maximally 0.1 mg/mL when mixed with infusion fluids. The reason is that when the concentration is higher than 0.1 mg/mL bumetanide will precipitate unless the pH of the preparation is maintained. The solubility of (non-ionised) bumetanide is 0.1 mg/mL or even lower. The licensed product contains alkaline additives in order to reach a concentration of 0.5 mg/mL. If these additives are diluted, the pH becomes too low, which may cause precipitation of non-ionised bumetanide.
Theophylline can be dissolved by salt formation with ethylenediamine or other amines. Previously, ethylenediamine theofyllinate (aminophylline) was used in oral preparations. Soluble double salts of theophylline can be prepared using sodium acetate and sodium glycinate. However, excellent absorption is achieved after oral administration of theophylline as such, for example in capsules, so administration as a solution does not seem to be necessary from a biopharmaceutical viewpoint. After absorption, at a physiological pH of approximately 7.4 there is obviously no difference in the degree of ionisation of the substance whether it was administered as such or as a salt. Therefore, no differences in physiological activity between an active substance and its salt are expected. However differences in solubility and dissolution rate and differences in absorption and absorption rate may generally influence the earlier stages of administration and lead to a difference in bioavailability. In addition, the counter ion may induce (undesirable) side-effects. The use of ethylenediamine was abandoned because of the sensitising properties, even after oral use [10]. In addition, it might be toxic, being a secondary amine.
18.1.2 Solubility and Salt Formation
Not all salts exhibit a good aqueous solubility. A number of inorganic salts having a relatively low molecular weight and a low water solubility are listed in Table 18.6. Also the solubility product often is given (Table 18.7). This allows us to determine the effect of other ions in the solution on the solubility of a given substance, for example, when sodium carbonate is added to a solution of magnesium chloride. Also the reduction of the solubility of the poorly soluble calcium carbonate can be calculated when a certain amount of the readily soluble sodium carbonate or calcium chloride is added. This reduction in the solubility of, in this case, calcium carbonate is also known as the common ion effect.
Table 18.6
Solubility of some Mineral Salts in Water in grams per Litre
22 °C | 38 °C | |
|---|---|---|
CaSO4.2H20 | 2.41 | 2.22 |
CaCO3 | 0.014 | 0.018 |
Ca3(PO4)2 | 0.02 | Not available |
CaHPO4.2H2O | 0.316 | Not available |
Ca(H2PO4)2.H2O | 18 | Not available |
MgSO4.7H2O | 710 | 910 |
MgCO3 | 0.106 | Not available |
MgHPO4.7H2O | 3 | 2a |
Table 18.7
Solubility Product of some Mineral Salts in Water
Solubility product (S)a | pS (= – logS) | |
|---|---|---|
CaSO4 | 7.1 × 10−5 | 4.15 |
CaCO3 | 5.0 × 10−9 | 8.30 |
Ca3(PO4)2 | 2.1 × 10−33 | 32.7 |
MgCO3 | 6.8 × 10−6 | 5.17 |
Mg3(PO4)2 | 6.5 × 10−5 | 4.18 |
Mg3(PO4)2 | 3.5 × 10−5 b | 4.46 |
An example of this can be found in solutions for parenteral nutrition that contain calcium and phosphate ions (see Sect. 13.9.2). At the pH of parenteral nutrition mixtures dihydrogen phosphate and monohydrogen phosphate will both be present. The solubility of calcium dihydrogen phosphate is 18 g/L and that of calcium monohydrogen phosphate 0.3 g/L.
As long as the pH of the mixture remains below 6.4, precipitation is not likely to occur. But for instance at a pH of 7.4, 60 % of the phosphate will be present in the form of monohydrogen phosphate, with an increasing risk of precipitation. Therefore, it is always best to check the solubility of the product.
Solubilities of many active substances are listed in Merck Index [6] and in Martindale [11]. When a pharmaceutical preparation contains various salts there may be (multiple) combinations of ions that are incompatible and may result in the formation of a precipitate. For example, after addition of a chloride salt to a chlorhexidine digluconate solution, the insoluble salt chlorhexidine chloride is formed resulting in precipitation. Exact data on this are hard to find. In general, the risks of precipitation are high for combinations of large positive and negative ions. Examples are carmellose anion and lauryl sulfate, which is a component of Lanette wax.
Insoluble salts can be made to mask an unpleasant taste or to prevent local irritation of the gastrointestinal tract. Well-known examples are ferrous fumarate suspension and potassium hydrogen tartrate suspension. In Sect. 5.4.10 more examples of insoluble salts to mask unpleasant tastes are discussed.
18.1.3 Solubility in Non-aqueous Solvents
When the aqueous solubility of an active substance is too low, it can be dissolved in a different solvent or mixture of solvents, which is compatible with the route of administration. The solubility of a lipophilic substance (a substance which dissolves well in the oil or fat but poorly in water) can be increased by making the dissolution medium (water) less polar by the addition of less polar but water-miscible solvents. Often mixtures of water, ethanol and propylene glycol are used. Also glycerol and macrogol (polyethylene glycol) can be used. The polarity of a solvent can be expressed by its dielectric constant, ε (for examples see Table 18.8, the higher the dielectric constant, the higher the polarity).
Table 18.8
Dielectric Constants of Some Solvents
Solvent: | Dielectrical constant, ε (25 °C) |
|---|---|
Water | 79 |
Glycerol | 43 |
Propylene glycol | 32 |
Ethanol | 24 |
Macrogol 400 | 12 |
The dielectric constant of a mixture of solvents can be calculated as the sum of the dielectric constants of its components, each multiplied by the volume fraction of that solvent. The dielectric constant of a mixture of solvents A, B, … is thus:
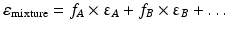
where fA, fB … are the volume fractions of the solvents A, B, respectively, and εA, εB, … the dielectric constants of the solvents A, B, …, respectively.
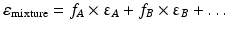
(18.7)
This equation can be used when the composition of a liquid mixture is to be changed, while keeping the dielectric constant the same. For example, assume that an active substance dissolves in a mixture of 20 % v/v water and 80 % v/v ethanol. As such a large volume percentage of ethanol is not desirable for many pharmaceutical applications; it has to be reduced to 20 % v/v. In order to maintain the dielectric constant, macrogol 400 can be used to replace a large part of the ethanol. The volume percentages of water and macrogol 400 can be calculated as follows:
Original mixture:
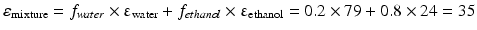 Adjusted mixture:
Adjusted mixture:
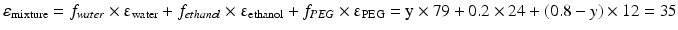 It follows that the volume fraction of water, y, is 0.31 and the volume fraction of the macrogol 400, (0.8 – y), 0.49. The composition of the adjusted mixture by volume percentage is thus: water/ethanol/ macrogol 400 = 31/20/49.
It follows that the volume fraction of water, y, is 0.31 and the volume fraction of the macrogol 400, (0.8 – y), 0.49. The composition of the adjusted mixture by volume percentage is thus: water/ethanol/ macrogol 400 = 31/20/49.
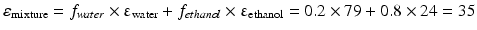
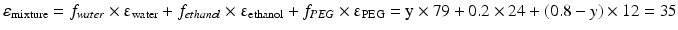
Pharmaceutical examples of solutions where a relatively poorly water soluble substance is dissolved in a mixture of solvents are injections with diazepam or digoxin (Table 18.9). In both of these preparations a mixture of ethanol, propylene glycol and water is used as the solvent.
Digoxin | 0.025 g |
Citric acid monohydrate | 0.075 g |
Disodium phosphate dodecahydrate | 0.450 g |
Ethanol (96 %) | 10 g |
Propylene glycol | 40 g |
Water for injections | ad 100 mL |
Paracetamol in an oral solution could at first be dissolved in 85 % glycerol (Table 18.10)
Paracetamol (500-90) | 2.4 g |
Ethanol (96 per cent) | 8.1 g |
Glycerol (85 per cent) | 74 g |
Raspberry flavouring (local standard) | 0.1 g |
Sodium (S)-lactate solution 600 g/kg | 6.65 g |
Sorbitol, liquid (crystallising) | 30.75 g |
Total | 122 g (= 100 mL) |
The relationship between the solvent medium, the pH and the pKa can be clearly illustrated using barbiturates as examples. Phenobarbital can be dissolved in water as its sodium salt. This requires a pH of 10 or higher. At this pH (it appears that) barbiturates decompose by ring-opening under the formation of malonylurea derivatives. The shelf life of such aqueous barbiturate solutions for oral administration is therefore limited to approximately 1 week. In addition, heat sterilisation of an aqueous solution for injection is not possible at this pH. In the formulation of injections, this problem has been solved by improving the solubility at slightly alkaline pH through the addition of a less polar solvent mixture e.g. a mixture of propylene glycol and ethanol.
In a mixture of 35 % v/v water, 35 % v/v propylene glycol and 30 % v/v ethanol at a pH of 8.9, the solubility of phenobarbital at room temperature is approximately 11 % w/v. An example of a formula for a phenobarbital injection of 50 mg/mL is given in Table 18.11. The pH is usually adjusted to a value between 7 and 8. Phenobarbital in these injections is thus partially in the ionised form. The non-ionised form is dissolved by the organic solvents.
Phenobarbital | 5.0 g |
Ethanol (96 %) | 31.5 mL |
Propylene glycol | 35.0 mL |
Sodium hydroxide solution 2 M (local standard) | q.s. |
Water for injections | ad 100 mL |
An alternative way to prepare solutions of lipophilic substances is to use solvents that are not miscible with water such as oils or esters of wax alcohols.
18.1.4 Solubility and Complex Formation
Sometimes two substances strongly interact (non-covalent) with each other in solution. In these cases complexes are formed whose solubility is different from that of the individual components. For example, iodine is only soluble in water in the form of a complex with iodide ions or with povidone. Iodinated povidone has the additional advantage that its solutions do not irritate the skin, as is the case for solutions where iodine is dissolved by complexation with potassium iodide.
Cyclodextrins are another category of substances that are used for complex formation. Cyclodextrins are ring-shaped oligosaccharides consisting of six, seven or eight glucose units referred to as alpha-, beta-, and gammacyclodextrin, respectively (see Fig. 18.2 for the chemical structure of betacyclodextrin) [15].
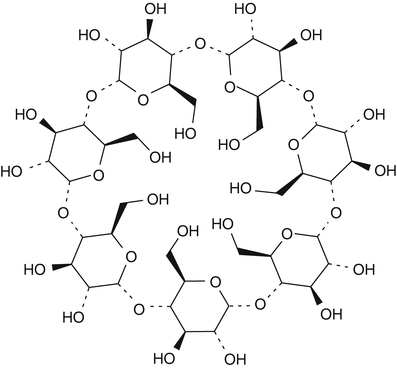

Fig. 18.2
Chemical structure formula of betadex (betacyclodextrin)
The Ph. Eur. has a monograph for betacyclodextrin: Betadex. Cyclodextrin forms a hollow truncated cone structure which is hydrophilic at the outside and contains a non-polar cavity into which lipophilic molecules fit (Fig. 18.3).
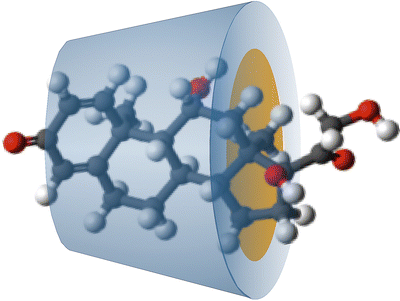

Fig. 18.3
Schematic representation of a betadex–prednisolone complex
The diameter of the non-polar cavity increases when cyclodextrin contains more glucose units. As a consequence, small lipophilic substances form better complexes with cyclodextrins having a small non-polar cavity and large lipophilic substances better with cyclodextrins having a large non-polar cavity. On the outside, cyclodextrins are polar by which they are fairly soluble in water. The aqueous solubility of cyclodextrins can be affected by derivatisation. Hydroxypropylbetacyclodextrin (Hydroxypropylbetadex Ph. Eur.) for example dissolves much better in water than the non-derivatised betadex (betacyclodextrin). Thus, the aqueous solubility of lipophilic molecules increases after complexation with cyclodextrins. By selecting the right combination of active substance and cyclodextrin, the solubility of poorly water-soluble substances can be increased.
Amongst other applications, cyclodextrins are used for the oral administration of lipophilic active substances. By complexing piroxicam with cyclodextrin a product is formed which shows an enhanced dissolution rate and therefore a more rapid absorption. An itraconazole oral mixture containing cyclodextrin has been developed to guarantee sufficient absorption of the active substance. Cyclodextrins are also used in parenteral preparations. Fluasteron is an antineoplastic agent which is preferably administered by injection to the patient at a concentration of 1,000 micrograms per millilitre. Its aqueous solubility, however, is only 0.045 microgram per millilitre. With a 20 % w/v hydroxypropylbetacyclodextrin solution, the desired concentration can be achieved [16].
18.1.5 Solubility of Derivatives
Derivatisation is a method of changing the properties of a molecule by means of a chemical reaction where an additional group is covalently coupled. By derivatisation, the solubility of substances can be either decreased or increased. In pharmacy, esters are important derivatives. This will be explained in greater detail on the basis of corticosteroids of which the C21-alcohol group can be esterified. These esters are not effective but should first be hydrolysed in the body. The rate of hydrolysis of esters in solution is strongly pH dependent. In a strongly acid or alkaline environment hydrolysis rapidly occurs. In vivo, the hydrolysis is catalysed by esterases.
Esters of corticosteroids with a polyvalent acid group, for example succinic acid or phosphoric acid, are soluble in their salt form. This is because most of the non-esterified acid groups are deprotonated when sufficiently high pH is chosen. Examples of corticosteroids which are esterified with polybasic acids are hydrocortisone sodium succinate, prednisolone sodium phosphate and dexamethasone sodium phosphate. In an aqueous medium with a pH of about 7 or higher, hydrocortisone sodium succinate is largely ionised and thus fairly soluble. At this pH, however, the hydrolysis of the ester is quite fast (this ester is most stable at a pH of about 4.5). As a result, dissolved in water, this substance is unstable and therefore its shelf life is limited.
In aqueous solution, prednisolone sodium phosphate and dexamethasone sodium phosphate are more stable than hydrocortisone sodium succinate. At a pH of about 8, the acid groups are sufficiently ionised to make the substance very soluble, while the phosphate ester is reasonably stable at this pH. Water soluble corticosteroids are mainly used in parenteral preparations, eye drops, oral mixtures and enemas. Examples are prednisolone oral mixtures and dexamethasone injections.
In order to increase their lipid solubility, corticosteroids have been esterified with monocarboxylic (fatty) acids. Examples include hydrocortisone acetate, beclomethasone dipropionate and betamethasone isovalerate. For triamcinolone, the following method has been developed to make the substance lipophilic: the hydroxyl groups at the C16 and C17-position of triamcinolone are used to form a cyclic acetal (Fig. 18.4). Although the formed substance, triamcinolone acetonide, is not a fatty acid ester, with regard to lipid solubility it behaves as such.
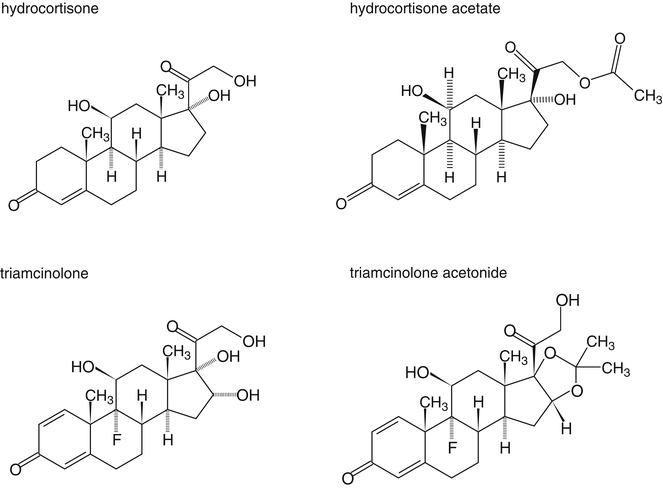

Fig. 18.4
Chemical structure formulas of hydrocortisone, hydrocortisone acetate, triamcinolone and triamcinolone acetonide
Fatty acid esters of corticosteroids may be used for the preparation of depot injections, either as oily solutions or aqueous suspensions. The nature of the fatty acid, in particular the length of the carbon chain, determines, to a large extent, its solubility and therefore its release and absorption rate into the bloodstream. In addition, in the case of corticosteroids, solutions or microcrystalline suspensions in either oil or water are used for intra- or periarticular injection.
Dermatology is another important field where fatty acid esters of corticosteroids are applied. Examples are creams with hydrocortisone acetate and triamcinolone acetonide, respectively. These fat-soluble derivatives are used because they show better penetration into the lipophilic stratum corneum of the skin.
Lipophilic esters of corticosteroids either suspended in water or dissolved in ethanol, propylene glycol, or macrogol 300 are applied in eye and ear drops, respectively. Table 18.12 gives an example of an aqueous suspension containing 1 % micronised hydrocortisone acetate.
Hydrocortisone acetate (micronised) | 1 g |
Benzalkonium chloride | 0.001 g |
Disodium edetate | 0.1 g |
Disodium phosphate dodecahydrate | 0.04 g |
Povidone | 2.5 g |
Sodium chloride | 0.85 g |
Sodium dihydrogen phosphate dihydrate | 0.03 g |
Water, purified | ad 100 mL |
Flumetasone pivalate and fludrocortisone acetate are commercially available as solutions in macrogol and a mixture of glycerol and propylene glycol, respectively.
The aqueous solubility of free, not esterified, corticosteroids and their lipophilic esters do not differ substantially. However, their solubility in ethanol is better. Examples are: hydrocortisone, prednisolone and dexamethasone. These free corticosteroids are mainly used in solid oral dosage forms. Hydrocortisone is applied in Acid Ear Drops with Hydrocortisone 1 % FNA (Table 18.13), because the underivatised steroid dissolves in propylene glycol, in contrast to its acetylated derivative. Although the lipophilic versions/variants are preferred in dermatological preparations, the free corticosteroids may also be applied.
Hydrocortisone (micronised) | 1 g |
Acetic Acid (30 %) DAC | 2.4 g |
Propylene glycol | 96.6 g |
Total | 100 g |
18.1.6 Solubility and Supersaturation
If the solubility of a substance increases with temperature, its dissolution rate can be enhanced by heating. When a saturated solution is obtained at an elevated temperature, it will be supersaturated after cooling. Also solutions that are prepared at room temperature can become supersaturated when they have to be stored in the refrigerator because of their chemical instability. It may happen that supersaturation does not immediately result in crystallisation. Such a solution is called metastable and sooner or later crystallisation will occur. This process can proceed faster if solid particles are present in the solution. These solid particles may act as crystallisation nuclei and so initiate the crystallisation process.
The rate of crystallisation increases when the difference between the temperature at which the solution is prepared and the storage temperature increases. This is because the driving force for crystallisation will increase when the temperature difference increases. Supersaturation can occur in starting materials or intermediates, but supersaturated compositions are also used in therapy. Some relevant examples will be briefly discussed below.
Liquid Sorbitol 70 % (crystallising) is a supersaturated starting material. Before using/processing this product in preparations the operator should check whether crystallisation has occurred. Crystals can be dissolved by heating and cooling again. Using a crystallised solution in several portions at different times will lead to a too low sorbitol concentration in the first portions, while in subsequent portions the concentration will be too high if the crystals have been dissolved again. Thus, when using a crystallised material in preparations, there is a risk that the content in the final product will not be correct.
Calcium gluconate 100 mg/mL is an example of a supersaturated injection solution.
Mannitol 20 % w/v is an example of a supersaturated solution for infusion. The solution should be inspected for the presence of crystals. As said, the crystals can be dissolved by heating and cooling again.
Magnesium Citrate Oral Solution 80 mg/mL FNA (Table 18.14) is a supersaturated solution of magnesium citrate. The patient should be warned that crystallisation can take place after about 2 weeks, or earlier when the preparation is stored in the refrigerator. Magnesium citrate mixture USP has a similar formula.
Magnesium carbonate, light | 3.00 g |
Citric acid monohydrate | 8.33 g |
Lemon Spirit BP | 0.40 g |
Syrup B.P. | 10 g |
Water, purified | ad 100 mL |
Given the risks of crystallised products, the use of supersaturated solutions in pharmaceutical preparations should be avoided as much as possible.
18.2 Rheology
The rheology describes the flow behaviour of fluids. When a force is exerted on a liquid, it will start to flow. The resistance to flow is called dynamic viscosity but in practice it is usually simply referred to as viscosity. Consider a cube of liquid composed of slices like a stack of cards (Fig. 18.5).
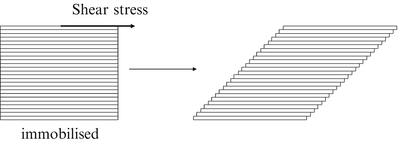

Fig. 18.5
Effect of shear stress on a cube of liquid
When the bottom of the cube is immobilised and a shear force is applied at the top, the upper slice will get the maximum speed, the slice underneath a little less speed, and so on, until the bottom slice which does not move. Consequently, there is a velocity gradient, D (shear rate). According to the Newton’s law (18.8), viscosity (η) is defined as the force exerted per unit area (τ) (shear stress) divided by the shear rate (D). The dimension of viscosity is Pascal.second (Pa.s), but in practice the derived dimension millipascal.second (mPa.s) is generally used.
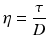
Rheology and viscosity are important for a proper understanding of the stability of disperse systems and for the accuracy of the dosage of liquid preparations.
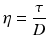
(18.8)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


