(1)
Faculty of Biomedical Engineering, Czech Technical University in Prague, Kladno, Czech Republic
(2)
J. Heyrovský Institute of Physical Chemistry v.v.i., Academy of Sciences of the Czech Republic, Prague, Czech Republic
Abstract
Studies of lateral diffusion are used for the characterization of the dynamics of biological membranes. One of the techniques that can be used for this purpose is fluorescence correlation spectroscopy (FCS), which belongs to the single-molecule techniques. Unfortunately, FCS measurements, when performed in planar lipid systems, are associated with a few sources of inaccuracy in the determination of the lateral diffusion coefficient. The main problems are related to the imperfect positioning of the laser focus relative to the plane of the sample. Another source of inaccuracy is the requirement for external calibration of the detection volume size. This protocol introduces a calibration-free method called Z-scan fluorescence correlation spectroscopy (Z-scan FCS), which is based on the determination of the diffusion time and particle number in steps along the optical (z-) axis by sequential FCS measurements. Z-scan FCS could be employed for diffusion measurements in planar membrane model systems—supported phospholipid bilayers (SPBs) and giant unilamellar vesicles (GUVs) and also in biological membranes. A result from measurements in SPBs is also presented in the protocol as a principle example of the Z-scan technique.
Key words
Z-scan fluorescence correlation spectroscopySupported phospholipid bilayersLateral diffusionFCS diffusion lawHumpolíčková plotMicrodomains1 Introduction
This chapter is dedicated to Z-scan fluorescence correlation spectroscopy (Z-scan FCS) which is based on fluorescence correlation spectroscopy (FCS); therefore we mention the basic principles of FCS at first. FCS is an experimental technique which was introduced in the early 1970s [1–4], but has become widespread only much later when confocal microscopes equipped with single-photon detectors with low noise, lasers with high temporal stability, and high-quality objectives became available [5–7]. Such instrumentation based on confocal microscopes is the most common in FCS nowadays.
Thanks to the confocal setup, where a pinhole is positioned in the image plane and is adjusted to overlap with the image of the focal spot, the signal from out-of-focus fluorescence is suppressed. Fluorescence emission from a dye is effectively collected by the detector only from a small volume element of the sample (detection volume), which is typically about 1 μm3 (1 fl) or smaller [5, 6, 8–10]. The size and shape of this effective detection volume is given by the so-called point-spread function, which is the product of the excitation light intensity distribution within the sample and of the light-collection efficiency, which is determined by the detection optics (especially by the confocal aperture) [5, 6, 10, 11]. The radius of the detection volume within the focal plane (the xy plane) is diffraction limited and ranges from 200 to 300 nm. The characteristic dimension along the optical axis of the microscope (the z-axis) is a few micrometers [5, 6, 10–16]. The profile of the laser beam within the sample is Gaussian in the x and the y directions and Lorentzian in the z-direction, but the shape of the effective detection volume is often approximated by a three-dimensional Gaussian [5, 9, 10, 17].
A typical source of the signal in FCS measurements is the diffusion of a few molecules through the detection volume, resulting in fluctuations in the fluorescence signal above the level of the background noise. The basic scheme of the FCS procedure starts by recording the intensity fluctuations with sufficient temporal resolution (at least an order of magnitude better than the timescale of the studied process), followed by the analysis of this recorded signal via autocorrelation functions G(τ). The physically relevant parameters, i.e., diffusion time τ D and particle number N, are then extracted from the obtained G(τ) by nonlinear fitting with an appropriate theoretical model taking into account the processes which may occur in the sample. The standard deviation of the fit of the autocorrelation curve can be obtained using the method described by Wohland et al. [18].
The normalized autocorrelation function G(τ) (see Eq. 1) is calculated from recorded time traces of fluorescence intensity I(t). G(τ) indicates the probability of finding a molecule in the detection volume at time t + τ, given a molecule was present there at time t. Pointed brackets in Eq. 1 represent averaging over all values of t:
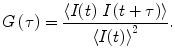
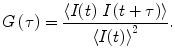
(1)
The shape of the autocorrelation function is given by the timescale of the fluctuations of the fluorescence intensity I(t) originating from the detection volume. The sources of intensity fluctuations are translational diffusion into and out of the detection volume, ligand–macromolecule binding, rotational diffusion, internal macromolecule dynamics, intersystem crossing to nonfluorescent triplet state, and excited-state reactions [19]. Fluctuations due to diffusion occur on a timescale of hundreds of microseconds to seconds, while fluctuations due to photochemical processes are much faster. This enables separation each of their contributions to the recorded time traces [5, 6, 20–22].
The detection volume in the case of confocal FCS has been described above. The theoretical model of autocorrelation function G(τ) for three-dimensional Brownian diffusion in a Gaussian volume element is given by [7]
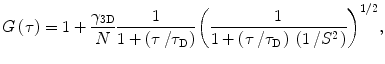
where the structure parameter S is the ratio ω z /ω 0 of the characteristic dimensions of the detection volume along the optical z-axis and in the xy plane, respectively. ω z and ω 0 are defined as distances at which the intensity drops by factor 1/e 2. τ D is the diffusion time, and N is the particle number (number of fluorescent particles within the detection volume). Correction factor γ 3D is defined by Thompson [7] to take into account the intensity profile in the focus, and it depends on experimental geometry. For a three-dimensional Gaussian profile γ 3D equals 2−3/2 [7]. The dimensions of the detection volume can be determined by a calibration measurement of the diffusion of a molecule with known diffusion coefficient D, fitting the data to Eq. 2 and using Eq. 3 [17].
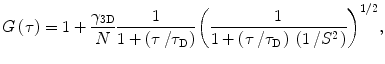
(2)
Diffusion coefficient D is an important parameter for mobility description of molecules in biological membranes. Coefficient D can be extracted directly from the experimentally obtained τ D by using the following expression:
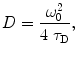
where ω 0 is the radius of the detection volume and is defined as the radial distance from the optical axis, at which intensity drops by 1/e 2 [17].
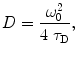
(3)
If the transition of fluorophores to nonfluorescent triplet state due to intersystem crossing cannot be neglected, Eq. 2 has to be extended by an average fraction of dye molecules in the triplet state T and an intersystem crossing relaxation time τ T into following fitting function [23, 24]:
![$$\begin{array}{lll}{G_{\mathrm{ T}}}\left( \tau \right) = 1+\left[ {1-T+T\exp \left( {{{{-\tau }} \left/ {{{\tau_{\mathrm{ T}}}}} \right.}} \right)} \right]\frac{{{\gamma_{{3\mathrm{ D}}}}}}{{N\left( {1-T} \right)}}\frac{1}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}}}}} \right.}} \right)}}\cr {{\left( {\frac{1}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}}}}} \right.}} \right)\;{{{\left( {{1 \left/ {S } \right.}} \right)}}^2}}}} \right)}^{{{1 \left/ {2} \right.}}}}. \end{array}$$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00284.gif)
![$$\begin{array}{lll}{G_{\mathrm{ T}}}\left( \tau \right) = 1+\left[ {1-T+T\exp \left( {{{{-\tau }} \left/ {{{\tau_{\mathrm{ T}}}}} \right.}} \right)} \right]\frac{{{\gamma_{{3\mathrm{ D}}}}}}{{N\left( {1-T} \right)}}\frac{1}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}}}}} \right.}} \right)}}\cr {{\left( {\frac{1}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}}}}} \right.}} \right)\;{{{\left( {{1 \left/ {S } \right.}} \right)}}^2}}}} \right)}^{{{1 \left/ {2} \right.}}}}. \end{array}$$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00284.gif)
(4)
The expression for the autocorrelation function is simplified when the diffusion is restricted to two dimensions, for example, in phospholipid bilayers or other planar systems. Unfortunately, when FCS is measured in these structures, it is accompanied by a few artifacts (see below). In case of two-dimensional diffusion, Eq. 4 can be simplified into [7, 25]:
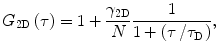
where the correction factor γ 2D is 0.5 in the case of the two-dimensional Gaussian profile [7].
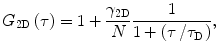
(5)
If introduction of intersystem crossing into two-dimensional Eq. 5 is necessary, the parameters T and τ T extend the equation to [17, 23–25]:
![$$ {G_{2\mathrm{ D}\mathrm{ T}}}\left( \tau \right) = 1+\left[ {1-T+T\;\exp \left( {{{{-\tau }} \left/ {{{\tau_{\mathrm{ T}}}}} \right.}} \right)} \right]\frac{{{\gamma_{{2\mathrm{ D}}}}}}{{N\left( {1-T} \right)}}\frac{1}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}}}}} \right.}} \right)}}. $$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00286.gif)
![$$ {G_{2\mathrm{ D}\mathrm{ T}}}\left( \tau \right) = 1+\left[ {1-T+T\;\exp \left( {{{{-\tau }} \left/ {{{\tau_{\mathrm{ T}}}}} \right.}} \right)} \right]\frac{{{\gamma_{{2\mathrm{ D}}}}}}{{N\left( {1-T} \right)}}\frac{1}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}}}}} \right.}} \right)}}. $$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00286.gif)
(6)
In case that M fluorophores with different diffusion times and detection efficiency contribute to the recorded signal, the following general equation should be used [7, 22, 25]:
![$$ {G_{2\mathrm{ D}\mathrm{ TM}}}\left( \tau \right) = 1+\frac{{{\gamma_{{2\mathrm{ D}}}}\sum\limits_{i=1}^M {{{{\left( {\frac{{{Q_i}}}{{{Q_1}}}} \right)}}^2}{F_i}\;{g_i}\left( \tau \right)} }}{{N\;{{{\left[ {\sum\limits_{{\acute{i}=1}}^M {\frac{{{Q_i}}}{{{Q_1}}}{F_i}} } \right]}}^2}}}, $$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00287.gif)
where F i is fraction of fluorophores diffusing with diffusion time τ Di , and Q i represents their detection efficiency which depends on quantum yields, extinction coefficients, and overlap of emission spectra with transmission region of the optical filters in the detection pathway. Term g i (τ) incorporates triplet parameters and diffusion time for i-fluorophore into Eq. 7 and is defined as [7, 22, 25]:
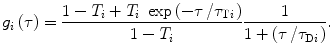
![$$ {G_{2\mathrm{ D}\mathrm{ TM}}}\left( \tau \right) = 1+\frac{{{\gamma_{{2\mathrm{ D}}}}\sum\limits_{i=1}^M {{{{\left( {\frac{{{Q_i}}}{{{Q_1}}}} \right)}}^2}{F_i}\;{g_i}\left( \tau \right)} }}{{N\;{{{\left[ {\sum\limits_{{\acute{i}=1}}^M {\frac{{{Q_i}}}{{{Q_1}}}{F_i}} } \right]}}^2}}}, $$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00287.gif)
(7)
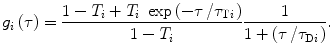
(8)
The probability of errors introduced to the fits of the autocorrelation function using Eq. 7 increases with increasing number (M) of components due to the higher number of free parameters [26, 27].
Equation 7 is reduced when only one type of fluorophore is present within the sample, but it could have two different diffusion times (for instance when a fraction of fluorophores F 1 is bound to larger molecules and the rest is free). If it can be assumed that Q and triplet properties are not affected by binding, Eq. 7 is simplified in [7, 23]:
![$$ \begin{array}{lll}{G_{2\mathrm{ D}\mathrm{ T}}}\left( \tau \right) = 1+\left[ {1-T+T\;\exp \left( {{{{-\tau }} \left/ {{{\tau_{\mathrm{ T}}}}} \right.}} \right)} \right]\frac{{{\gamma_{{2\mathrm{ D}}}}}}{{N\left( {1-T} \right)}}\\ \left( {\frac{{{F_1}}}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}1}}}} \right.}} \right)}}+\frac{{1-{F_1}}}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}2}}}} \right.}} \right)}}} \right),\end{array} $$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00289.gif)
where τ D1 is the diffusion time of bound fluorophore, and τ D2 is analogously for free fluorophore.
![$$ \begin{array}{lll}{G_{2\mathrm{ D}\mathrm{ T}}}\left( \tau \right) = 1+\left[ {1-T+T\;\exp \left( {{{{-\tau }} \left/ {{{\tau_{\mathrm{ T}}}}} \right.}} \right)} \right]\frac{{{\gamma_{{2\mathrm{ D}}}}}}{{N\left( {1-T} \right)}}\\ \left( {\frac{{{F_1}}}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}1}}}} \right.}} \right)}}+\frac{{1-{F_1}}}{{1+\left( {{\tau \left/ {{{\tau_{\mathrm{ D}2}}}} \right.}} \right)}}} \right),\end{array} $$](/wp-content/uploads/2017/03/A299540_1_En_28_Chapter_Equ00289.gif)
(9)
The first source of artifacts in FCS is related to high excitation intensities which are not necessary for performing measurement as proved in [11, 28, 29]. High excitation intensities can even lead to artifacts due to photobleaching, when a time trace of fluorescence intensity during the measurement is no longer stationary (which is one of the assumptions behind the above mentioned theoretical models of autocorrelation functions). The probability, that fluorescent species undergo photobleaching, is related to the time spent in the illuminated volume (which is longer for slowly diffusing molecules) and grows with increasing laser power. Optical saturation is the other effect related to the excitation intensity. This saturation occurs when an increased number of molecules within the detection volume is not in the ground state but in an excited or triplet state, leading to the loss of proportionality between excitation and fluorescence intensities [5, 6, 10, 11, 28].
Other artifacts that can influence the results of FCS are caused by deviations of the real shape of the detection volume from its form assumed in the derivation of the above mentioned theoretical models for the diffusion coefficient. A detailed discussion of the sources of those artifacts (like laser beam astigmatism, refractive index mismatch between the sample and objective immersion medium, or imperfect pinhole adjustment) and numerical simulations showing how they influence the physically relevant parameters obtained by FCS (τ D and N) is presented in studies by Jörg Enderlein and his group.[5, 6, 11, 28]
The most important source of artifacts in FCS measurements in phospholipid bilayers and other planar system is positioning of the sample with respect to the focus along the z-axis. Those artifacts are specific for planar samples and are not encountered in FCS investigations of three-dimensional diffusion in bulk. The thickness of a membrane bilayer is about 5 nm and therefore several orders of magnitude smaller than the characteristic dimension ω z of the detection volume. Different positions of bilayer with respect to the focus result in different diameters of illuminated bilayer area (thanks to divergence of laser beam) and thus in different measured values of τ D and N (Fig. 1). There are different ways to overcome this problem, for example, the recently developed two-focus FCS [9, 30, 31], which requires a nonstandard setup using two alternatively pulsed polarized lasers. The Z-scan method [17, 29, 32], on the other hand, can be easily performed with a standard FCS setup allowing scanning along the z-axis.
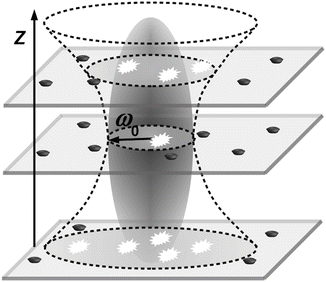

Fig. 1
Scheme of Z-scan positioning problem of planar samples. Z-positioning of planar sample out of the focus plane results in a larger detection area due to the divergence of the laser beam and, thus, higher N and τ D. The interior of the ellipsoid marks the volume where photon detection efficiency is higher than 1/e 2 of its maximum
Z-scan fluorescence correlation spectroscopy (Z-scan FCS) overcomes the positioning problem and is a calibration-free method; this means that there is no requirement for the calibration measurement of the detection volume dimensions. Z-scan FCS can be employed for diffusion monitoring of labelled membrane lipids or membrane associated molecules such as proteins and also for characterizing the binding kinetics of these entities to planar membrane model systems—supported phospholipid bilayers (SPBs) and giant unilamellar vesicles (GUVs)—as well as to suitable biological membranes. When comparing GUVs and SPBs, Przybylo et al. [29] found the diffusion in GUVs to be more than 2 times higher than in SPBs, which suggests coupling of the bilayer with the support; on the other hand, GUVs membranes suffer from thermal undulations [33]. Another typical field of biophysics investigations is the study of the dependence of the D of proteins or lipids, on their content in membrane composition.
The Z-scan method is based on the determination of τ D and N in steps along the optical axis (z-axis) by sequential FCS measurements (see Fig. 2). Assuming a Lorentzian profile of the effective detection volume along the z-axis, dependencies of τ D and N on the z-coordinate (Fig. 3) are the following [34, 35]:
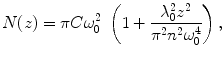
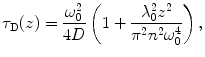
where C is the average concentration of diffusing fluorescence molecules in the illuminated area, ω 0 is the 1/e 2 radius of the beam in the focal plane (the waist of the beam; the term 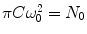 is the particle number in the beam waist), λ 0 is the wavelength of the excitation light in vacuum, z is the axial distance between the sample position and the focal plane, and n is the refractive index of the medium [17, 22, 25, 32, 36].
is the particle number in the beam waist), λ 0 is the wavelength of the excitation light in vacuum, z is the axial distance between the sample position and the focal plane, and n is the refractive index of the medium [17, 22, 25, 32, 36].

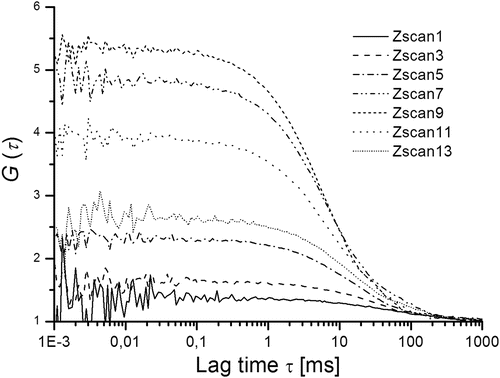
Fig. 2
Resulting Z-scan autocorrelations. Measurements with 0.2 μm steps were performed with starting position (Z-scan 1) 1 μm below estimated z-position of the focal plane. It can be concluded that Z-scan 8 and Z-scan 9 were performed when the focus plane and the sample were in the nearest vicinity (where autocorrelation amplitude G(0) is the highest, thanks to its indirect proportionality to N)

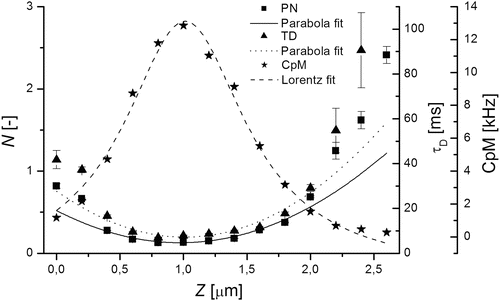
Fig. 3
Dependencies of N(z)—triangle, τ D(z)—squares and the photon count per molecule—stars (CpM—the total fluorescence count rate divided by N) on sample positioning are depicted. Values N(z) and τ D(z) are fitted with parabolas described by Eqs. 10 and 11 while CpM(z) is fitted with a Lorentzian function describing the axial intensity profile in the focus
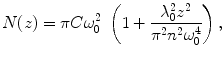
(10)
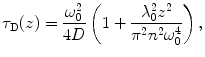
(11)
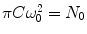 is the particle number in the beam waist), λ 0 is the wavelength of the excitation light in vacuum, z is the axial distance between the sample position and the focal plane, and n is the refractive index of the medium [17, 22, 25, 32, 36].
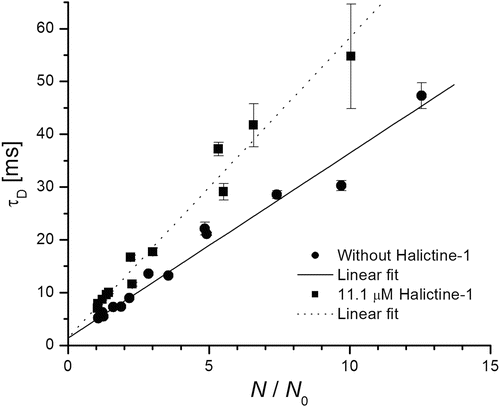
is the particle number in the beam waist), λ 0 is the wavelength of the excitation light in vacuum, z is the axial distance between the sample position and the focal plane, and n is the refractive index of the medium [17, 22, 25, 32, 36].A theoretical model, called the FCS diffusion law, was formulated by Wawrezinieck et al. [37] for characterization of hindered lateral diffusion in membranes. This model is valid only when membranes contain diffusion-preventing obstacles in low concentrations, and their size is sufficiently small in comparison to the ω 0 value. Otherwise, if this assumption is not fulfilled, it is necessary to take into account a theoretical fitting model for description of anomalous diffusion. Humpolíčková et al. utilized diffusion law analysis (based on determination of diffusion times in dependence on alterations in size of detection area) and character of the Z-scan FCS (changes in dimensions of the illuminated membrane area while performing scanning in the z-direction) and elegantly combined the diffusion law equation [37] with Eqs. 10 and 11. Resulting equation expresses the theoretical linear dependence of τ D on z-position [32]:
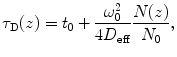
where D eff is the effective diffusion coefficient, N(z) number of particles in the detection area at a given z-coordinate, and t 0 is intersection point with the diffusion time axis, and its value gives information about the presence of obstacles in the membrane [32, 37].
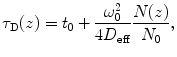
(12)
The basic issue of this combination method is plotting the dependency of the measured τ D(z) on N(z)/N 0 (sometimes called Humpolíčková plots) and fitting these data by Eq. 12. Figure 4 is an example of such a Humpolíčková plot of pure SPBs and SBPs after treatment by halictine-1 peptide [38, 39]. The obtained value t 0 indirectly reveals information about the presence and dimensions of membrane structures. Monte Carlo simulations made by Wawrezinieck et al. [37] showed that if fluorophores move by free Brownian diffusion in membranes without any inhomogeneities, then t 0 = 0; the same holds if only fully impermeable obstacles are in the membrane (they only lead to a decrease of D). Secondly they assumed isolated lipid rafts—microdomains in membrane; those act as a trap for diffusing fluorescent species, which can enter them, and their movement is hindered inside the microdomains. In such cases t 0 value is positive. Finally simulations were done for the case that membranes are divided into corrals (within which fluorophores diffuse freely) separated by partially permeable barriers. t 0 < 0 was found in that case. The absolute value of t 0 yields information on dimensions of the obstacles [22, 36, 37].