As you saw in Chapter 1, one of the main uses of epidemiology is to identify the causes of disease, and this is of fundamental importance in all areas of public health – if we can work out what is causing ill health then we can work to prevent it. In Chapter 2 we looked at the ways in which we can measure the occurrence of disease and touched on some ways in which we can compare different populations. However, while measuring the occurrence of a disease in a population can tell us about the health of that population, it does not directly shed much light on the underlying causes of the disease. To identify the aspects of people or their environment (exposures) that might lead to the onset of disease, we need to compare disease occurrence in groups with and without the exposures of interest. In Chapter 4 we looked at some of the study designs that we can use to do this; now we will look more closely at the measures we use to quantify the associations between ‘exposures’, or potential causes of disease, and the disease itself. By quantifying the association between an exposure and disease we can start to make judgements as to whether the exposure might actually cause the disease (we will discuss causality in more detail in Chapter 10). If we believe that it is causing disease, we can then identify the importance of that exposure in terms of its overall effect on the health of a community.
In this chapter we will look at the ways in which we calculate, use and interpret these ‘measures of association’, so-called because they describe the association between an exposure and a health outcome. An understanding of these measures will help you to interpret reports regarding the causes of ill health and the effects of particular exposures or interventions on the burden of illness in a community. Note that, while we will discuss the measures in the context of an ‘exposure’ and ‘disease’, they can be used to assess the association between any measure of health status and any potential ‘cause’.
You will often see measures of association referred to as ‘effect’ measures. Although this name suggests a cause and effect relationship (i.e. that the exposure causes the outcome to occur), we are actually only measuring associations and these may or may not be causal (see Chapter 10).
Looking for associations
We all know that smoking is a cause of lung cancer, but might it also increase the risk of stroke? To answer this question we could compare the incidence of stroke in a group of women who smoke with that in a group of non-smokers.
Exchangeability: Throughout this chapter we assume that the groups we are comparing are comparable in all ways except with regard to the exposure of interest – i.e. that they are exchangeable. We will discuss some of the issues we face when they are not exchangeable when we discuss bias and confounding in Chapters 7 and 8.
Table 5.1 displays data from a cohort study in which the investigators followed a large group of women for several years (person-years of observation). They classified the women as never smokers, ex-smokers and current smokers, recorded how many women had a stroke during the follow-up period and calculated the incidence rate of stroke in each group.
The answers to these questions reflect the two main ways in which we can compare smokers and non-smokers. First, ex-smokers were 1.6 times (27.9 ÷ 17.7) and current smokers were 2.8 times (49.6 ÷ 17.7) as likely to have a stroke as never smokers during the follow-up period. An alternative way to look at the data would be to say that, all other things being equal, if the smokers had never smoked we would have expected them to have the same rate of stroke as the never smokers, i.e. 17.7/100,000 person-years. This means that, compared with never smokers, there were an extra 10.2 strokes per 100,000 person-years (27.9 – 17.7) in ex-smokers and an extra 31.9 strokes per 100,000 person-years (49.6 – 17.7) in current smokers.
What we calculated above were, first, the rate ratio and, second, the rate difference for the association between smoking and stroke. These measures give us two different ways of quantifying the relation between an exposure and a disease. The rate ratio tells us how many times higher the rate of disease is in one group than in another group (e.g. current smokers are almost three times as likely to have a stroke as never smokers). This gives an indication of the strength of the association and can help us to decide whether smoking could be a cause of stroke. The rate difference tells us how much extra disease occurred in one group compared with another group (e.g. there were an extra 32 strokes per 100,000 person-years among current smokers compared with non-smokers). If we believe that smoking is a cause of stroke then this extra disease can be attributed to the fact that the women are smokers and, theoretically, it would not have occurred if they had never smoked. This information gives some sense of the potential value of a preventive intervention, in this case a programme aimed at stopping women from taking up smoking. (Of course, if such an intervention were successful it would reduce the incidence of many diseases, not just stroke.)
It is important to remember that ratio and difference measures give us very different perspectives on a given situation. Look back to Box 5.1 at the start of the chapter. Men would probably prefer to look at the ratio or relative measure: they do three times more housework now than 40 years ago. In contrast, women would focus on the difference or absolute measure: men may do three times more laundry now than 40 years ago, but they still do an average of only 5 minutes (3.5 minutes extra) per day.
His view: Australian men do three times more housework today than they did 40 years ago …
Her view: Australian men spend 5 minutes a day on laundry now compared to 1.6 minutes 40 years ago – an extra 3½ minutes a day …
Ratio measures (relative risk)
The cholera was therefore 14 times as fatal at this period amongst persons having the impure water of the Southwark and Vauxhall Company, as amongst those having the purer water from Thames Ditton (Snow, 1855) (from Box 1.7).
People who ate cold chicken at the youth camp were almost four times as likely to become ill as people who did not eat cold chicken (from Table 1.2).
Ratio or relative measures tell us how many times as likely it is that someone who is exposed to something will develop a certain disease or experience a particular health outcome compared (or relative) to someone who is not exposed. They do not tell us anything about the actual amount of disease occurring in either group. They provide information about the strength of the association between the exposure and the outcome and, as you will see in Chapter 10, a strong association is more suggestive that the exposure is actually causing the outcome. In the example above, the rate ratio for stroke and current smoking was 2.8. This is a fairly strong association and would add weight to an argument that smoking was actually causing strokes, although it is not as compelling as the much stronger relation between smoking and lung cancer, for which the rate ratio for current smoking is somewhere between 10 and 15.
As the example shows, ratio measures are very easy to calculate – you simply divide the frequency of disease (or of any health outcome) in the group that is exposed to the factor of interest by the frequency in the group that is not exposed to it. This can be done using either of the measures of disease incidence that you met in Chapter 2. If you divide two incidence rates you end up with a rate ratio (as for the stroke example above); if you divide two incidence proportions or risks then it is a risk ratio. It is also possible to divide two measures of prevalence to calculate a prevalence ratio. Note that you must always divide two measures of the same type – you cannot usefully divide an incidence rate by an incidence proportion.
Rate ratios
As you saw above, a rate ratio is calculated by simply dividing the incidence rate of disease in a group of people exposed to the factor of interest (often denoted by a subscript ‘e’) by the incidence rate in a group of people who are not exposed to the same factor (denoted by a subscript ‘o’):
 (5.1)
(5.1)This factor could be a potential cause of disease, it could be a characteristic of a person, such as their age or where they live, or it could be something that influences behaviour. Equally, it could be a preventive measure or, in the clinical context, a drug or other treatment that we hope will reduce the incidence of disease.
Risk ratios
Similarly, the risk ratio (also called the relative risk) is calculated by dividing the incidence proportion or risk of disease in an exposed group by the incidence proportion in an unexposed group:
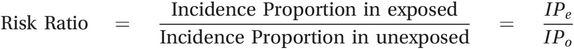 (5.2)
(5.2)In this trial, the risk ratio was 28.3% ÷ 20.0% = 1.4; those who took aspirin were 1.4 times as likely to develop blood clots as those who did not take aspirin. A risk ratio of 1.0 would mean that there was no difference between the groups, so those taking aspirin were 40% more likely to develop blood clots than those not taking aspirin (in the context of clinical epidemiology this may be described as the relative risk increase or RRI). If aspirin had reduced the risk of blood clots then we would have expected to see a risk ratio of less than 1.0. Clearly this intervention did not work the way the investigators had hoped it would.
This approach can be used much more widely than in the search for the causes of disease. As an example, a trial was conducted in three general practices in the UK to find out whether telephoning patients to offer them an appointment for immunisation against influenza would increase immunisation uptake rates (Hull et al., 2002). In this study, attending for immunisation was the outcome of interest and receiving a telephone call was the exposure. A total of 1318 patients aged 65–74 years were randomly assigned to two groups. Patients in one group (n = 660) received a telephone call from the receptionist at their general practice inviting them to make an appointment for immunisation (the intervention or exposed group). Patients in the other group (n = 658) were not called (the control or unexposed group). The investigators then waited to see who turned up for immunisation. They found that 328 of the patients who received a phone call attended, as did 288 of those who did not receive a call.
The easiest way to look at these data is in the form of a ‘2 × 2 table’. These tables are usually set out so that the two columns show the numbers of people with and without the outcome of interest while the rows show the numbers in the exposed and unexposed groups (Table 5.2).
| Exposure | Outcome | ||
|---|---|---|---|
| Immunised | Not immunised | % immunised | |
| Received a call | 328 | 332 | 50 |
| No call | 288 | 370 | 44 |
| Total | 616 | 702 | 47 |
What percentage of patients attended for immunisation (the incidence proportion) in each of the two groups?
How many times as likely were patients to attend if they had received a personal call to make an appointment than if they had not been telephoned?
In the intervention group 50% of patients were immunised, compared with 44% of those in the control group (despite the intervention the immunisation rates were still below the government target of 60%). This means that patients who received an invitation were 1.14 times (50% ÷ 44%) as likely to attend for immunisation. This measure is still a relative risk because it has the same structure – the incidence proportion (or risk) of a particular health outcome in one group is divided by the incidence proportion in a second group. In this case the word ‘risk’ seems less appropriate, but the term relative risk is still regularly used.
Prevalence ratios
As you saw when we discussed prevalence surveys in Chapter 3 and cross-sectional studies in the previous chapter, it is also possible to use measures of prevalence instead of incidence to compare the burden of disease in two groups and in this situation you end up with a prevalence ratio:
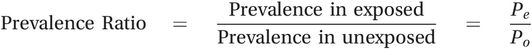 (5.3)
(5.3)As we discussed in Chapter 2, measures of prevalence are harder to interpret than measures of incidence and for this reason prevalence ratios are used much less frequently than rate and risk ratios.
A note about relative risks
We noted above that the term relative risk is synonymous with risk ratio. In practice, it is also commonly used to describe a rate ratio, because both the rate ratio and the risk ratio compare the amount of disease in one group relative to that in another. If a disease is rare (incidence proportion or risk less than 1%), then the rate ratio and risk ratio will be almost identical; if it is not so rare then the risk ratio will be closer to 1.0 than the rate ratio although, in practice, there is little difference as long as the incidence proportion is less than about 10%. The three terms rate ratio, risk ratio and relative risk are also commonly and conveniently abbreviated as RR. When we use the term relative risk it will refer to both the rate ratio and the risk ratio.
It is also worth noting that, although relative risks are also used in the context of clinical trials, several other related measures are also used in the field of clinical epidemiology (Box 5.2).
In 1998, Botti et al. reported a trial of the use of pressure bandages for patients undergoing coronary angiography. Some of their results are shown in Table 5.3.
| Pressure bandages | Total | Number with bleeding | Incidence proportion or event rate |
|---|---|---|---|
| Yes | 519 | 18 | EERa = 3.5% |
| No | 556 | 37 | CERb = 6.7% |
| Total | 1075 | 55 | 5.0% |
The relative risk of bleeding among those given pressure bandages compared with those without is 3.5 ÷ 6.7 = 0.52. This tells us that those given pressure bandages were about half as likely to develop bleeding as those who were not given bandages. The results of treatment trials are sometimes also reported as a relative risk reduction (RRR). This is the amount by which the treatment has reduced the relative risk and it is calculated by subtracting the relative risk from 1.0. It may then be expressed as a percentage by multiplying by 100:
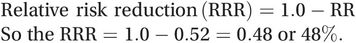 (5.4)
(5.4)Alternatively, it can be calculated directly from the incidence proportion or, using the terminology of clinical epidemiology (see Box 2.4 on page 43), the event rates among the experimental (EER) and control (CER) groups:
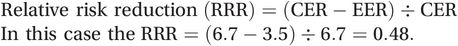 (5.5)
(5.5)In other words, use of the pressure bandages has reduced the risk of bleeding among patients undergoing coronary angiography by 48%. Obviously, the greater the RRR the better the intervention.
For studies with a positive association (RR > 1.0) the results are turned around to give what is logically called the relative risk increase (RRI). In the aspirin study discussed previously, aspirin increased the risk of bleeding by 40% (RR = 1.4).
Note that you will see associations described in this way in all fields of epidemiology, e.g. ‘The risk of disease was 20% lower among those who exercised more’. It is a simple, informative mode of description that just happens to have been given a separate name in the area of clinical epidemiology.
Standardised incidence and mortality ratios
We discussed these measures in Chapter 2 (pages 56–58) because of the links between direct and indirect standardisation, but they also deserve a mention here because they compare the rate of disease (or death) in two populations and so, in effect, are also measures of relative risk.
Difference measures (attributable risk)
As we noted above, the relative risk tells us nothing about the actual amount of disease that is occurring. If the incidence proportions or risks of disease in exposed and unexposed groups were 0.5% and 0.1%, respectively, the relative risk would be 5.0. Similarly, if the risks were 50% and 10%, the relative risk would also be 5.0. The major difference between these two situations is obvious: the actual amount of disease that is occurring is vastly different – in fact, in the second example it is 100 times greater. This vital public health information cannot be obtained from the relative risk.
The approach to measuring the excess amount of disease occurring among those exposed to a potential risk factor is just as intuitive, and the measures are as simple to calculate as the relative risk. As you saw in the smoking and stroke example at the start of the chapter, we can calculate the extra amount of disease that is occurring in the exposed group by simply subtracting the incidence in the unexposed group (IRo, CIo or background risk) from the incidence in the exposed group (IRe, CIe). This can again be done using either of the measures of disease incidence (incidence rate or incidence proportion) that you met in Chapter 2. If you are subtracting two incidence rates (as in the stroke example) you end up with a rate difference, whereas if you are subtracting two incidence proportions or risks (as in the immunisation example) you have a risk difference. These measures are also sometimes described as the excess rate and excess risk as they measure the extra disease that only occurs in the presence of the exposure. If we think that it is reasonable to assume that the excess disease can be attributed to the exposure, i.e. the exposure is causing the disease, then both of these measures can also be described as the attributable risk (in the same way that relative risk is used to describe both rate ratios and risk ratios).
Rate differences
Consider the smoking and stroke example again (Table 5.1). Compared with never smokers, there were an extra 10.2 strokes (27.9 – 17.7) per 100,000 person-years in ex-smokers and an extra 31.9 strokes (49.6 – 17.7) per 100,000 person-years in current smokers. These differences are illustrated in Figure 5.1. The left-hand bar (a) shows the incidence rate of stroke in non-smokers. This is often called the reference or background rate because it reflects the natural occurrence of the disease in an unexposed population. We expect this to operate on all members of the population regardless of their smoking status, and this is shown for the ex- and current smokers. This lets us visualise directly the extra burden of stroke added by past and present smoking habits. Thus the second bar shows the extra incidence of stroke in ex-smokers (b) that is presumably due to the fact that the women had smoked in the past. Similarly, the third bar shows the far greater added rate of stroke in current smokers (c) that is attributable to their smoking. This extra disease is simply the difference between the rate in the exposed group (smokers) and the rate in the unexposed group (non-smokers). The total rate of disease in exposed individuals is therefore the sum of the background rate (due to other causes) and the additional rate due to the exposure in question.
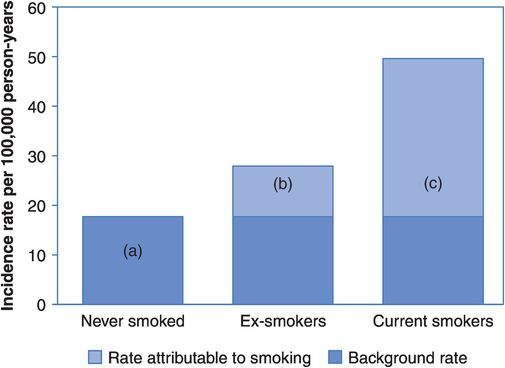
Attributable risks: the results of a study of smoking and stroke
If the groups differ only in their smoking habit and if we believe that smoking is actually causing strokes to occur then we can say that the extra disease in the smokers is attributable to their smoking – if they had not smoked then it would not have occurred. This rate difference is also called the attributable risk (AR) because it measures the actual amount of disease that can be attributed to a particular exposure:
Rate difference or attributable risk
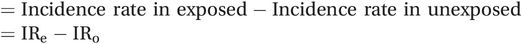 (5.6)
(5.6)Risk differences
Look back to the example of immunisation against influenza in Table 5.2.
What percentage of patients in the intervention group would have been expected to attend for immunisation even if they hadn’t received a phone call (background ‘risk’)?
What extra percentage of patients presumably attended only because they had received a call (i.e. how many attendances could be attributed to the phone call)?
We would have expected 44% of patients in the intervention group to go for immunisation even if the practice receptionists had not called to offer them an appointment. We can therefore say that an extra 6% of patients (50% – 44%) in the intervention group presumably went for immunisation only because they had received a call, i.e. their immunisation can be attributed to this. Here we have calculated a risk difference (as opposed to a rate difference) because we are subtracting incidences proportions (or risks):
Risk difference or attributable risk
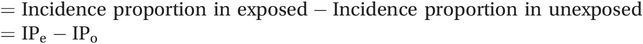 (5.7)
(5.7)Again we are assuming the two groups are exchangeable and that if the intervention group had not been invited to go for immunisation their rate of attendance would have been the same as that in the control group.
Attributable fractions (AFs)
In addition to the attributable risk, it may also be informative to consider the proportion of cases in the exposed group that would not have occurred in the absence of the exposure. This measure is often called the attributable fraction or attributable proportion, although you will also come across it described as the attributable risk percent. To calculate the attributable fraction you simply divide the attributable risk by the incidence in the exposed group:
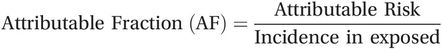
or 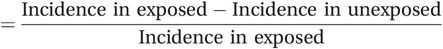
Again, this can be done using either the incidence rate or the incidence proportion:
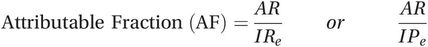 (5.8)
(5.8)Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



