(1.1)
where E is Young’s modulus, σ is axial strain, and ε is axial stress. Young’s modulus can be used to predict compression as a result of axial stress. Typical values of Young’s modulus for human tissues are given in Table 1.1 (Hoskins et al. 2010). When a material is stressed, its breadth contracts and its length extends. Poisson’s ratio, v, is defined from this contraction and extension. It is given by
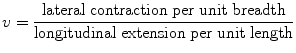
(1.2)
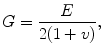
(1.3)
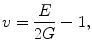
(1.4)
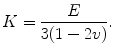
(1.5)
Table 1.1
Young’s modulus values for human tissues
Tissue | E (kPa) |
|---|---|
Artery | 700–3,000 |
Cartilage | 790 |
Tendon | 800 |
Healthy soft tissues (Breast, kidney, liver, prostate) | 0.5–70 |
Cancer in soft tissues (Breast, kidney, liver, prostate) | 20–560 |
For a triaxial stress, the total normal strains are given by
![$$ \begin{aligned} \varepsilon_{x} & = \frac{{\sigma_{x} }}{E} - \frac{{v\sigma_{y} }}{E} - \frac{{v\sigma_{z} }}{E} = \frac{1}{E} \left[ {\sigma_{x} - v\left( {\sigma_{y} + \sigma_{z} } \right)} \right] \\ \varepsilon_{y} & = \frac{{\sigma_{y} }}{E} - \frac{{v\sigma_{x} }}{E} - \frac{{v\sigma_{z} }}{E} = \frac{1}{E} \left[ {\sigma_{y} - v(\sigma_{x} + \sigma_{z} )} \right] \\ \varepsilon_{z} & = \frac{{\sigma_{z} }}{E} - \frac{{v\sigma_{x} }}{E} - \frac{{v\sigma_{y} }}{E} = \frac{1}{E} \left[ {\sigma_{z} - v(\sigma_{x} + \sigma_{y} )} \right] \\ \end{aligned} $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equa.gif)
![$$ \begin{aligned} \varepsilon_{x} & = \frac{{\sigma_{x} }}{E} - \frac{{v\sigma_{y} }}{E} - \frac{{v\sigma_{z} }}{E} = \frac{1}{E} \left[ {\sigma_{x} - v\left( {\sigma_{y} + \sigma_{z} } \right)} \right] \\ \varepsilon_{y} & = \frac{{\sigma_{y} }}{E} - \frac{{v\sigma_{x} }}{E} - \frac{{v\sigma_{z} }}{E} = \frac{1}{E} \left[ {\sigma_{y} - v(\sigma_{x} + \sigma_{z} )} \right] \\ \varepsilon_{z} & = \frac{{\sigma_{z} }}{E} - \frac{{v\sigma_{x} }}{E} - \frac{{v\sigma_{y} }}{E} = \frac{1}{E} \left[ {\sigma_{z} - v(\sigma_{x} + \sigma_{y} )} \right] \\ \end{aligned} $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equa.gif)
Alternatively, in matrix form,
![$$ \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ \end{array} } \right] = \frac{1}{E}\left[ {\begin{array}{*{20}c} 1 & { - v} & { - v} \\ { - v} & 1 & { - v} \\ { - v} & { - v} & 1 \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ \end{array} } \right]. $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equ6.gif)
![$$ \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ \end{array} } \right] = \frac{1}{E}\left[ {\begin{array}{*{20}c} 1 & { - v} & { - v} \\ { - v} & 1 & { - v} \\ { - v} & { - v} & 1 \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ \end{array} } \right]. $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equ6.gif)
(1.6)
By solving for the direct stresses it is obtained;
![$$ \left[ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ \end{array} } \right] = \frac{vE}{(1 - 2v)(1 + v)}\left[ {\begin{array}{*{20}c} {\frac{1 - v}{v}} & 1 & 1 \\ 1 & {\frac{1 - v}{v}} & 1 \\ 1 & 1 & {\frac{1 - v}{v}} \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ \end{array} } \right] . $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equ7.gif)
![$$ \left[ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ \end{array} } \right] = \frac{vE}{(1 - 2v)(1 + v)}\left[ {\begin{array}{*{20}c} {\frac{1 - v}{v}} & 1 & 1 \\ 1 & {\frac{1 - v}{v}} & 1 \\ 1 & 1 & {\frac{1 - v}{v}} \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ \end{array} } \right] . $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equ7.gif)
(1.7)
And the shear strain is given by
![$$ \left[ {\begin{array}{*{20}c} {\tau_{xy} } \\ {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right] = G \left[ {\begin{array}{*{20}c} {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right] $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equ8.gif)
where τ is shear stress, and γ is shear strain. The elastic constants, E, ν, and G, are related so that there are only two independent constants. The speeds at which mechanical waves propagate in a solid are given by the following equations (Postema 2011).
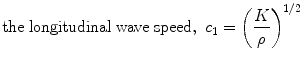
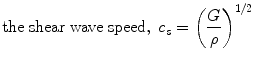
where ρ is the tissue mass density.
![$$ \left[ {\begin{array}{*{20}c} {\tau_{xy} } \\ {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right] = G \left[ {\begin{array}{*{20}c} {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right] $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equ8.gif)
(1.8)
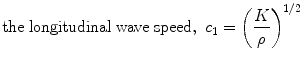
(1.9)
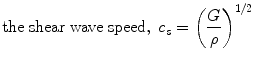
(1.10)
1.3 Basic Stiffness Data of Breast Tissue
The ability of a tissue to deform its shape when a mechanical force is applied and to recover its original shape after removing the force is referred to as the tissue elasticity. Tumor tissue is harder than normal tissue. In general, soft tissues are anisotropic, viscoelastic, and nonlinear. However, they are usually assumed as linear, elastic, and isotropic for the purpose of analytical simplification (Ophir et al. 2002; Gao et al. 1996). Soft tissues comprise both solid and fluid components, and so their mechanical properties are being somewhere between those of the materials. The ratio G/K of soft tissues is close to a few tenths for solid materials, where as that of liquid is zero. Poisson’s ratio for soft tissues is usually between 0.490 and 0.499 (Wells and Liang 2011), which make them mechanically alike to liquid. For most of the solids, the Poisson’s ratios are between 0.2 and 0.4 (Sarvazyan et al. 1995).
The values of Young’s modulus are usually reported, rather than those of shear modulus in the literature. This is because tissue is almost incompressible. The published data for Young’s moduli of breast tissues is listed in Table 1.2 (Krouskop et al. 1998). Most cancers feel stiffer on palpation because they have a lower strain value and a higher Young’s modulus. Breast tumors can have a much higher Young’s modulus than the surrounding normal tissue, they can be 4 to 10 or more times stiffer, and this ratio is called the relative Young’s modulus or the contrast.
Table 1.2
Stiffness measurements (kPa) of normal and abnormal breast tissues in vitro
Breast tissue type | 5 % pre-compression loading frequency | 20 % pre-compression loading frequency | ||||
|---|---|---|---|---|---|---|
0.1 | 1 | 4 | 0.1 | 1 | 4 | |
Normal fat (n = 40) | 18 ± 7 | 19 ± 7 | 22 ± 9 | 20 ± 8 | 20 ± 6 | 24 ± 6 |
Normal glandular (n = 31) | 28 ± 14 | 33 ± 11 | 35 ± 14 | 48 ± 15 | 57 ± 19 | 66 ± 17 |
Fibrous (n = 21) | 96 ± 34 | 107 ± 32 | 118 vs. 83 | 220 ± 88 | 233 ± 59 | 244 ± 85 |
Ductal CA (n = 23) | 22 ± 8 | 25 ± 4 | 26 ± 5 | 291 ± 67 | 301 ± 58 | 307 ± 78 |
Infiltrating ductal CA (n = 32) | 106 ± 32 | 93 ± 33 | 112 ± 43 | 558 ± 180 | 490 ± 112 | 460 ± 178 |
The elastic moduli of the different breast tissues did not change with the frequency of the applied displacement over the experimental range of the strain rates (Krouskop et al. 1998). It can be clearly shown in Table 1.2 that the breast fibrous tissues are stiffer than glandular tissues and they are in turn harder than adipose tissue. Tumors with the infiltrating ductal carcinomas are apparently stiffer than the tumors with ductal carcinomas.
1.4 Elastography
It is a direct imaging technique of the strain and Young’s modulus of tissues (Ophir et al. 1999; Gao et al. 1996; Sarvazyan 1993). The images produced by elastography are high-resolution images and called elastograms. Elastograms display the axial or lateral strains. The basic principal of elastography method will be described here.
In order to avoid the problems due to reflections, standing waves, and mode patterns, quasi-static stress is applied to the tissue. All points in the tissue experience a certain level of three-dimensional strains. Since a rapid compression is applied, only the elastic property is observed and slow viscous properties are neglected although tissues have viscoelastic properties. In elastography, quasi-static uniaxial stress is applied and the estimation of strain along the ultrasound beam (longitudinal strain) is considered in small tissue elements. If one or more of the tissue elements has different stiffness with the others, the level of strain in that element will be higher or lower. And if the tissue element is harder, then it will experience less strain than the softer one.
The longitudinal axial strain is estimated in one dimension from the analysis of ultrasound signals obtained from the medical ultrasound machine. To accomplish this estimation, the tissue is compressed with the ultrasonic transducer along the ultrasonic radiation axis by a small amount, and then the first set of digitized radio frequency (RF) echo lines reflected from the interesting tissue region is acquired, and then the second, post-compression set of echo lines from the same region of interest is acquired. Congruent echo lines are then subdivided into small temporal windows, which are compared pairwise by using cross-correlation techniques (Foster et al. 1990). From this comparison, the change in arrival time before and after compression can be estimated. Because of the small magnitude of applied stress, small distortions of the echo lines occur and the arrival time changes are also small. The local longitudinal strain is estimated as in Eq. 1.11 (Ophir et al. 1991).
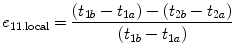
where t 1a = arrival time of pre-compression echo from the proximal window, t 1b = arrival time of pre-compression echo from the distal window, t 2a = arrival time of post-compression echo from the proximal window, and t 2b = arrival time of post-compression echo from the distal window.
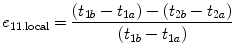
(1.11)
Since elastography is a method that is used to generate the new types of images, properties of elastograms are quite different from the properties of sonogram. Sonograms display the information related to the local acoustic backscatter energy from tissue components, and elastograms display the information related to its local strains, Young’s modulus or Poisson’s ratio. Figure 1.1 illustrates the general process of creating strain and modulus elastograms (Ophir et al. 1997, 1999). The input to elastography system is the tissue modulus distribution. The output can be either elastogram (strain image) or the modulus image. By applying quasi-static stress compression and restricting by mechanical boundary conditions, the tissue strain is obtained and this is measured with ultrasound system. The strain filter (SF) here is the selective filtering of the tissue strain with the contribution of the ultrasound system parameters (acoustical parameters) and signal processing parameters. The SF predicts the elastogram quality by specifying the elastographic signal-to-noise ratio (SNRe), sensitivity and the strain dynamic range at a given resolution (Varghese and Ophir 1997). The contrast-transfer efficiency (CTE) of the strain elastogram from SF is improved in recursive inverse problem solution block.
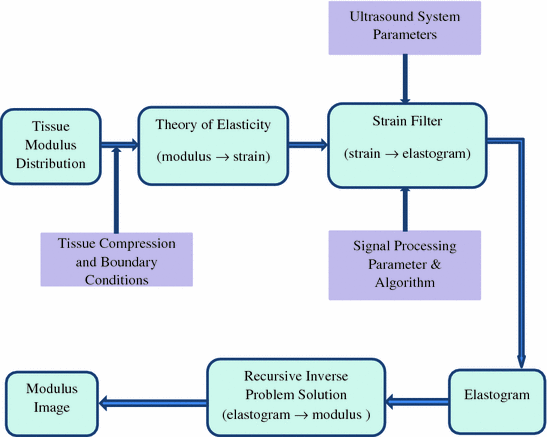

Fig. 1.1
Elastography system block diagram
1.5 Constant-Transfer Efficiency
Using ultrasonic techniques, some of the local longitudinal components of the strain tensor in the tissue can be determined. The strain elastogram represents only the distribution of tissue elastic moduli, and the local components of the stress tensor keep on as unknown (Ophir et al. 1999, 2002). The CTE is defined as the ratio of the observed (axial) strain contrast, C 0, measured from the strain elastogram, and the underlying true modulus contrast, C T , using a plane-strain-state model. By expressing in decibels, the ratio becomes a difference as
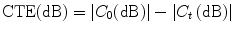
![$$ \begin{aligned} C_{t} & = \frac{{E_{t} }}{{E_{M} }} \\ \frac{1}{{C_{0} }} & = \left[ {\frac{(1 - 2v )}{{C_{t} + (1 - 2v)}} + \frac{2}{{1 + C_{t} (3 - 4v)}} } \right] \\ \end{aligned} $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equb.gif) where
where
CTE is normalized to the 0 dB, i.e., the maximum efficiency is reached at 0 dB for both hard and soft inclusions.
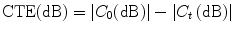
(1.12)
![$$ \begin{aligned} C_{t} & = \frac{{E_{t} }}{{E_{M} }} \\ \frac{1}{{C_{0} }} & = \left[ {\frac{(1 - 2v )}{{C_{t} + (1 - 2v)}} + \frac{2}{{1 + C_{t} (3 - 4v)}} } \right] \\ \end{aligned} $$](/wp-content/uploads/2017/03/A313638_1_En_1_Chapter_Equb.gif)
E t
target Young’s modulus
E M
background Young’s modulus
v
Poisson’s ratio.
1.6 Time Delay Estimation in Elastography
Time delays between pre-compression and post-compression echo signals are used to estimate the local tissue displacements, and these are in turn used to estimate the tissue strain. Peak of cross-correlation function between pre-compression and post-compression echo signals are applied to predict the time delays. The quality of the elastography is mainly determined from the quality of TDE. The random noises and the compression force needed for tissue strains introduce the errors in TDE. Then degradation of TDE is being occurred and that degrades the strain estimation.
In strain estimation and imaging, echo signal decorrelation is one of the major artifacts. Decorrelation errors are affected of the relative displacement of scatterers in three dimensions due to tissue compression. For small strains, post-compression echo signal stretching can be totally compensated for signal decorrelation. When the post-compression echo signal is stretched, all the scatters restore within the correlation window. Global uniform stretching could significantly improve the SNRe and expand the strain dynamic range in elastograms (Alam and Ophir 1997). In low-contrast targets and/or low strains, global uniform stretching produces quality elastograms. However, in high-contrast targets, significant over-stretching occurs in the areas of low strains, which causes noteworthy degradation of elastograms in these areas. For these situations, an adaptive axial stretching introduced in Alam et al. (1998a) becomes essential. But axial stretching can recover most of the decorrelation due to scatterer motion in the axial direction and cannot recover the decorrelation due to lateral and elevation motions. The decorrelation due to lateral motion may be compensated using a signal interpolation technique and large improvements in elastographic image quality is obvious (Konofagou and Ophir 1998). During post-compression signal stretching, decorrelation due to the unintended stretching of the transducer point-spread function (PSF) is occurred and the deconvolution filter is used to reduce this artifact (Alam et al. 1998b).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


