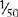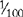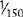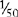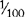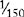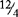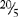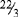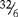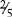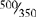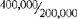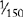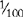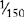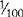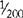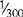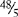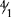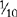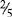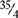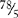INTRODUCTION TO BASIC MATH REVIEW
Objectives
OUTLINE
The basic math review assists nurses in converting Roman and Arabic numerals, multiplying and dividing fractions and decimals, and solving ratio and proportion problems and percentage problems. Nurses need to master basic math skills to solve drug dosage problems for the administration of medication.
A math test, found on pages 11 to 15, follows the basic math review. The test may be taken first, and, if a score of 90% or greater is achieved, the math review, or Part I, can be omitted. If the test score is less than 90%, the student should do the basic math review section. Some students may choose to start with Part I and then take the test.
Answers to the Practice Problems are at the end of Part I, before the Post-Math Test.
NUMBER SYSTEMS
Two systems of numbers currently used are Arabic and Roman. Both systems are used in drug administration.
Arabic System
The Arabic system is expressed in the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These can be written as whole numbers or with fractions and decimals. This system is commonly used today.
Roman System
Numbers used in the Roman system are designated by selected capital letters, e.g., I, V, X. Roman numbers can be changed to Arabic numbers.
Conversion of Systems
| Roman Number | Arabic Number |
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
The apothecary system of measurement uses Roman numerals for writing drug dosages. The Roman numerals are written in lowercase letters, e.g., i, v, x, xii. The lowercase letters can be topped by a horizontal line, e.g. 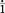 ,
, 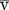 ,
,  ,
, 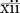 .
.
Roman numerals can appear together, such as xv and ix. Reading multiple Roman numerals requires the use of addition and subtraction.
Method A
If the first Roman numeral is greater than the following numeral(s), then ADD.
EXAMPLES
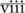 = 5 + 3 = 8
= 5 + 3 = 8
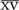 = 10 + 5 = 15
= 10 + 5 = 15
Method B
If the first Roman numeral is less than the following numeral(s), then SUBTRACT. Subtract the first numeral from the second (i.e., the smaller from the larger).
EXAMPLES
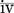 = 5 − 1 = 4
= 5 − 1 = 4
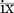 = 10 − 1 = 9
= 10 − 1 = 9
Some Roman numerals require both addition and subtraction to ascertain their value. Read from left to right.
EXAMPLES
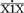 = 10 + 9 (10 − 1) = 19
= 10 + 9 (10 − 1) = 19
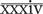 = 30 (10 + 10 + 10) + 4 (5 − 1) = 34
= 30 (10 + 10 + 10) + 4 (5 − 1) = 34
FRACTIONS
Fractions are expressed as part(s) of a whole or part(s) of a unit. A fraction is composed of two basic numbers: a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of parts.
EXAMPLES
Fraction:
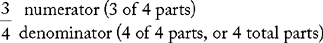
The value of a fraction depends mainly on the denominator. When the denominator increases, for example, from 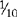 to
to 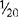 , the value of the fraction decreases, because it takes more parts to make a whole.
, the value of the fraction decreases, because it takes more parts to make a whole.
EXAMPLES
Which fraction has the greater value: ¼ or ⅙? The denominators are 4 and 6.
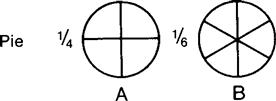
The larger value is ¼, because four parts make the whole, whereas for ⅙, it takes six parts to make a whole. Therefore ⅙ has the smaller value.
Proper, Improper, and Mixed Fractions
In a proper fraction (simple fraction), the numerator is less than the denominator, e.g., ½, ⅔, ¾,  . (When possible, the fraction should be reduced to its lowest terms, e.g.,
. (When possible, the fraction should be reduced to its lowest terms, e.g.,  = ⅓ [2 goes into 2 and 6].)
= ⅓ [2 goes into 2 and 6].)
In an improper fraction, the numerator is greater than the denominator, e.g., 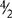 ,
, 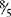 ,
, 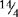 . (Reduce improper fractions to whole numbers or mixed numbers, e.g.,
. (Reduce improper fractions to whole numbers or mixed numbers, e.g., 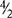 = 2 [
= 2 [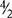 means the same as 4 ÷ 2];
means the same as 4 ÷ 2]; 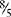 = 1⅗ [8 ÷ 5, 5 goes into 8 one time with 3 left over, or ⅗]; and
= 1⅗ [8 ÷ 5, 5 goes into 8 one time with 3 left over, or ⅗]; and 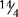 = 3
= 3 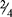 = 3½ [14 ÷ 4, 4 goes into 14 three times with 2 left over, or
= 3½ [14 ÷ 4, 4 goes into 14 three times with 2 left over, or 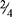 , which can then be reduced to ½].)
, which can then be reduced to ½].)
A mixed number is a whole number and a fraction, e.g., 1⅗, 3½. Mixed numbers can be changed to improper fractions by multiplying the denominator by the whole number, then adding the numerator, e.g., 1⅗ = 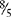 (5 × 1 = 5 +3 = 8).
(5 × 1 = 5 +3 = 8).
Fractions may be added, subtracted, multiplied, or divided. Multiplying fractions and dividing fractions are the two common methods used in solving dosage problems.
Multiplying Fractions
To multiply fractions, multiply the numerators and then the denominators. Reduce the fraction, if possible, to lowest terms.
EXAMPLES
PROBLEM 1:
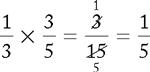
The answer is 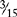 , which can be reduced to ⅕. The number that goes into both 3 and 15 is 3. Therefore 3 goes into 3 one time, and 3 goes into 15 five times.
, which can be reduced to ⅕. The number that goes into both 3 and 15 is 3. Therefore 3 goes into 3 one time, and 3 goes into 15 five times.
PROBLEM 2: 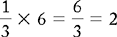
A whole number can also be written as that number over one (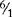 ). Six is divided by 3 (6 ÷ 3); 3 goes into 6 two times.
). Six is divided by 3 (6 ÷ 3); 3 goes into 6 two times.
PROBLEM 3: 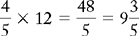
Dividing Fractions
To divide fractions, invert the second fraction, or divisor, and then multiply.
EXAMPLES
PROBLEM 1: 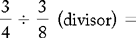
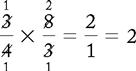
When dividing, invert the divisor ⅜ to 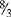 and multiply. To reduce the fraction to lowest terms, 3 goes into both 3s one time, and 4 goes into 4 and 8 one time and two times, respectively.
and multiply. To reduce the fraction to lowest terms, 3 goes into both 3s one time, and 4 goes into 4 and 8 one time and two times, respectively.
PROBLEM 2:
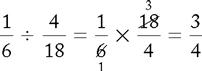
Six and 18 are reduced, or canceled, to 1 and 3.
PROBLEM 3:
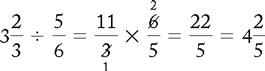
Change 3⅔ to fraction and invert ⅚ to 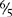 and then multiply.
and then multiply.
Reduce 3 and 6 to 1 and 2.
Decimal Fractions
Change fraction to decimal. Divide the numerator by the denominator.
PROBLEM 1:
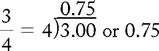
Therefore ¾ is the same as 0.75.
PROBLEM 2:
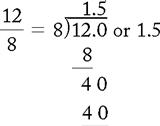
DECIMALS
Decimals consist of (1) whole numbers (numbers to the left of decimal point) and (2) decimal fractions (numbers to the right of decimal point). The number 2468.8642 is an example of the division of units for a whole number with a decimal fraction.
| Whole Numbers | Decimal Fractions | |||||||
| 2 | 4 | 6 | 8 | • | 8 | 6 | 4 | 2 |
| T | H | T | U | T | H | T | T | |
| h | u | e | n | e | u | h | e | |
| o | n | n | i | n | n | o | n | |
| u | d | s | t | t | d | u | ||
| s | r | s | h | r | s | T | ||
| a | e | s | e | a | h | |||
| n | d | d | n | o | ||||
| d | s | t | d | u | ||||
| s | h | t | s | |||||
| s | h | a | ||||||
| s | n | |||||||
| d | ||||||||
| t | ||||||||
| h | ||||||||
| s | ||||||||
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



 I ROMAN NUMERALS
I ROMAN NUMERALS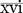
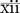
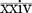
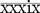
 II FRACTIONS
II FRACTIONS