, James Levitt1 and Pei-Hua Chung1, 2
(1)
Department of Physics, King’s College London, London, UK
(2)
Faculty of Life Sciences, University of Manchester, Manchester, UK
Abstract
Fluorescence can be characterized by its intensity, position, wavelength, lifetime, and polarization. The more of these features are acquired in a single measurement, the more can be learned about the sample, i.e., the microenvironment of the fluorescence probe. Polarization-resolved fluorescence lifetime imaging—time-resolved fluorescence anisotropy imaging, TR-FAIM—allows mapping of viscosity or binding or of homo-FRET which can indicate dimerization or generally oligomerization.
Key words
FAIMTR-FAIMPolarization-resolved FLIMTCSPCFluorescence spectroscopyFluorescence microscopyHomo-FRET1 Introduction
Fluorescence imaging techniques are powerful and versatile tools in the life sciences, because they use nonionizing radiation, are minimally invasive, and can be applied to living cells and tissues. Measurements can be made in situ, thus allowing access to biological function within a true physiological context [1–4].
In order to maximize the information available from a limited fluorescence photon budget, it is advantageous to record multiple fluorescence parameters—such as lifetime, spectrum, and polarization—in a single imaging experiment [5]. Fluorescence is polarized due to the existence of a transition dipole moment of the fluorophore and thus the electric dipole characteristics of the emission. Indeed, polarization-resolved fluorescence measurements have been performed since the 1920s [6]. When using fluorescence as a probe, polarization-resolved measurements can yield information on the properties of a sample that cannot be extracted by intensity and lifetime methods alone [7, 8].
In a polarization-resolved fluorescence microscopy experiment, a fluorescently labeled sample is excited using linearly polarized light, and the (time-resolved) fluorescence intensity is measured at polarizations parallel and perpendicular to that of the exciting light. The difference between the parallel and perpendicular fluorescence signal is due to depolarization of the fluorescence. The fluorescence anisotropy r is then defined as
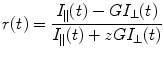
where I ||(t) and I ⊥(t) are the fluorescence intensity decays parallel and perpendicular to the polarization of the exciting light. The value of z depends on the NA of the microscope objective, where 1 ≤ z ≤ 2 (z = 1 for a high NA objective, z = 2 for a collimated beam) [9–16]. Although a rigorous treatment of the effect of high NA objectives to “see around” the fluorophore and therefore collect all three emission components I x , I y , I z leads to a slightly more complex description than Eq. 1 [10, 15, 17], this empirical approach is attractive due to its simplicity and similarity with that of a collimated beam and has worked well in our laboratory and others [18]. The empirical constant z is a function of the NA of the microscope objective and is chosen such that (1) a time-resolved fluorescence anisotropy decay starts at the correct initial anisotropy r 0 (as determined by spectroscopic measurements using collimated excitation light) and (2) the total fluorescence intensity decay I ||(t) + zI ⊥(t) is the same as a decay collected using collimated beams with magic angle detection such that polarization contributions are removed [18]. The denominator is proportional to the total fluorescence emission, and G accounts for differences in the transmission and detection efficiencies of the imaging system at parallel and perpendicular polarization. If necessary, an appropriate background has to be subtracted [19]. Due to the nature of the photoselection for absorption and emission transition dipoles, multiphoton excitation provides a greater dynamic range for anisotropy measurements than single photon excitation [20].
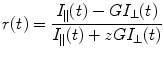
(1)
The depolarization of the fluorescence, i.e., the decay of the anisotropy r as a function of time, can either be due to the rotational diffusion of the fluorophore in its excited state before emission of a fluorescence photon or due to energy migration or homo-FRET.
1.1 Rotational Diffusion
The rotational diffusion of the fluorophore in its excited state before emission of a fluorescence photon depends on its volume and the viscosity and temperature of its environment. For a spherical molecule, r(t) decays as a single exponential and is related to the rotational correlation time θ according to
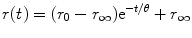
where r 0 is the initial anisotropy (maximum value is 0.4 for single photon excitation) and r ∞ accounts for a restricted rotational mobility. r ∞ = 0 for freely rotating fluorophores, e.g., in isotropic, homogeneous solution. For a spherical molecule in an isotropic medium, θ is directly proportional to the viscosity η of the solvent and the hydrodynamic volume V of the rotating molecule:
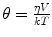
where k is the Boltzmann constant and T the absolute temperature. Therefore, if the volume of the fluorophore is known, the rotational correlation time can report on the viscosity of the fluorophore’s immediate environment. Alternatively, as the rotational diffusion can be slowed down by binding or sped up by cleavage, θ can yield information about the size of the tumbling unit. In addition, evidence of a hindered rotation of the fluorophore due to geometrical restrictions, e.g., in the cell membrane, can be gleaned from r ∞.
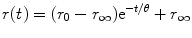
(2)
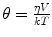
(3)
Note that the steady-state anisotropy is calculated from the fluorescence intensities, i.e., integrated fluorescence decays, from Eq. 1 and obeys the Perrin equation
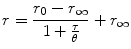
where τ is the fluorescence lifetime [21]. While the steady-state anisotropy is relatively easy to measure, and in particular to image, it may not be unambiguous to interpret in the absence of time-resolved measurements.
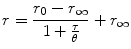
(4)
Steady-state fluorescence anisotropy imaging has, for example, been used to study viscosity, enzyme activity or binding in cells [22–29], and DNA digestion [30] or to identify FRET between fluorescent proteins [31–35]. However, it is difficult to obtain information about a hindered rotational mobility as indicated by a nonzero r ∞, and time-resolved measurements are needed to determine this parameter.
Time-resolved fluorescence anisotropy has been used on cells for single-point measurements [23, 36–38] and for mapping solvent interactions in microfluidic devices [39], as well as the viscosity in the cell cytoplasm [19, 21, 40] and membrane [41].
In the absence of rotational diffusion, i.e., in cases where τ/θ is small, polarization-resolved measurements can be used to elucidate the orientation of fluorophores, e.g., in the membrane [42, 43], muscle fibers [44], or in DNA [45]. In these cases, neither the depolarization due to Brownian rotational motion nor homo-FRET is measured but rather the angle between the electric vector of the light exciting the sample and the transition dipole moment of the static fluorophore, thus yielding its orientation.
1.2 Energy Migration or Homo-FRET
FRET can occur if the absorption spectrum of the acceptor overlaps with the emission spectrum of the donor, the fluorophores are in close proximity, and their orientation is favorable (i.e., orientation factor κ 2 ≠ 0 [46–48]), as extensively discussed in reference [49]. These conditions can apply to fluorophores with a small Stokes shift and hence lead to the donor and acceptor being the same type of fluorophore. Thus resonance energy transfer between the same type of fluorophore can take place, known as energy migration or homo-FRET. This phenomenon depolarizes the fluorescence emission [6] and has been exploited in single-point measurements and imaging, e.g., to monitor the proximity of isoforms of the glycosyl phosphatidylinositol (GPI)-anchored folate receptor bound to a fluorescent analogue of folic acid to study lipid rafts [50, 51], to monitor actin polymerization [52], or to image the aggregation of protein α-synuclein, relevant for Parkinson’s disease [53].
Time-resolved fluorescence anisotropy measurements to identify homo-FRET have been carried out to study conformational changes in G-protein-coupled receptors [54], dimerization [55], and quantification of protein cluster sizes [56–59], to show that a neuronal isoform of Venus-tagged calcium-calmodulin-dependent protein kinase-II (CaMKIIa) holoenzyme forms catalytic domain pairs, and to show that glutamate receptor activation in neurons triggers an increase in anisotropy consistent with a structural transition from a paired to unpaired conformation [60, 61] and to study the homodimerization of amyloid precursor protein at the plasma membrane, relevant for Alzheimer’s disease [62]. In these cases, it is advantageous to have negligible rotational diffusion (τ/θ is small), so that homo-FRET can be identified, see Fig. 1.
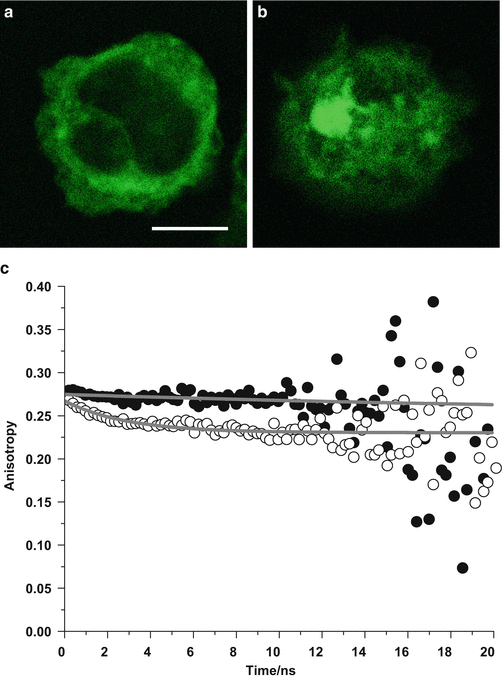

Fig. 1
Time and polarization-resolved fluorescence data from 3 μM rhodamine 123 in a 25/75 (V/V) methanol/glycerol mixture recorded using an inverted confocal laser scanning microscope with a 63× NA 1.2 objective and TCSPC detection. (a) Fluorescence decays recorded with polarization components parallel and perpendicular to that of the excitation light and (b) the time-resolved anisotropy decay created using Eq. 1 and the decays in (a)
For homo-FRET involving two fluorophores, and in the absence of any rotational diffusion, r(t) decays as a single exponential and is related to the FRET efficiency E TR according to [63]
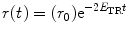
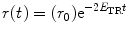
(5)
While hetero-FRET between different donors and acceptors to identify protein interaction can routinely be imaged with FLIM, mapping energy migration or homo-FRET to identify protein dimerization requires polarization-resolved FLIM, i.e., TR-FAIM. The only way to detect homo-FRET is by polarization measurements, because homo-FRET does not affect spectra or fluorescence lifetime—as long as the fluorescence lifetime of both fluorophores is the same—and thus cannot be identified by intensity and lifetime methods. If the fluorescence lifetimes of the two fluorophores are different, however, then FRET can be identified by fluorescence lifetime measurements [64, 65]. This has, for example, been done in the case of tryptophan to tryptophan homo-FRET in barnase, where the tryptophans are located in different environments yielding different fluorescent lifetimes [66].
Homo-FRET between fluorescent proteins can be extremely fast, 2 ps has been quoted for YFP [67], and is an indicator of protein dimerization or oligomerization, and TR-FAIM is the only technique which can image it.1
Anisotropy imaging can be performed as steady-state or time-resolved measurements in the time domain or frequency domain [68] using scanning or wide-field methods [5, 69, 70] and has been combined with spectral imaging [71]. Photon counting approaches are particularly attractive because of their excellent signal-to-noise ratio and single photon sensitivity [72–74].
The combination with TIRF with time-resolved fluorescence anisotropy measurements allows excitation with s– and p-polarized evanescent waves and provides spatial information on the fluorescence depolarization processes near an interface. This has, for example, facilitated the observation of membrane dyes in and out of plane [75, 76] and has indeed been combined with imaging [77].
2 Materials
2.1 Hardware
1.
Inverted Leica TCS SP2 confocal scanning microscope with internal analogue photomultiplier detectors.
2.
Coherent Mira 900 Ti:Sapphire femtosecond laser with a Verdi V6 pump laser or Hamamatsu PLP-10,470 ps pulsed diode laser excitation sources.
3.
Becker & Hickl SPC 830 board for time-correlated single photon counting (TCSPC) in 3 GHz, Pentium IV, 1 GB RAM computer with Windows. (The minimum requirements recommended by the manufacturer are PC Pentium, multi-core CPU.)
4.
Cooled Becker & Hickl PMC100-01 detector head based on Hamamatsu H5773P-01 photomultipliers, mounted on microscope’s X1 port, or hybrid detectors (external detectors).
5.
DCC 100 detector control module.
3 Methods
3.1 Align the Optical System
A schematic representation of the time-resolved fluorescence anisotropy experiment is shown in Fig. 2.
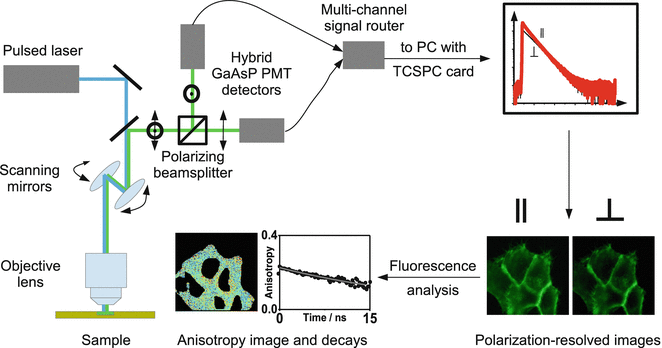

Fig. 2
Green fluorescent protein-labeled proteins in fixed leukocytes. (a) Monomeric proteins. (b) Clustered proteins. (c) Time-resolved fluorescence anisotropy decays. In the upper curve (filled black circles, corresponding to scan over confocal fluorescence image (a)), there is almost no depolarization of the fluorescence over time due to the restricted motion of the monomeric GFP in the fixed cell. In the lower curve (open circles, corresponding to scan over confocal fluorescence image (b)), a fast decay component in the GFP fluorescence anisotropy decay appears, which is the characteristic signature of GFP undergoing homo-FRET. Scale bar 5 μm
Ensure that the incident laser (excitation beam) is linearly polarized and that this linear polarization state is retained to the highest degree possible at the sample plane. Accurate alignment through the microscope scan head along with the half-wave plate and linear polarizer combination in the incident beam path will ensure that this is the case and allow for rotation of the polarization of the beam.
Ensure that the polarization components of the detected light, parallel and perpendicular, are split adequately by the polarizing beam splitter. Using unpolarized light (e.g., from a lamp) to test the detection, the intensity of each polarization component after the beam splitter should be equal. Circularly polarized light, created by placing a quarter waveplate in the beam, can also be used. Ensure correct alignment of cleanup polarizers in each arm of the detection.
Select a suitable microscope objective for the sample of interest you wish to study. Phase objectives should be avoided due to the phase plate, and note that high NA objectives partially depolarize the light (an effect that can be corrected for, as described in the context of Eq. 1).
Select the correct emission filter/wavelength for the sample of interest.
Check polarized fluorescence decays of a test sample. Select time window size, adjust delay to place peak at the beginning of the time window, and select the number of time channels, typically 4,096 for recording single decays and 256 for imaging.
3.2 Measure the G-Factor
Place a suitable test sample of a small molecule fluorophore in solution on the microscope stage. An example of a suitable test sample with peak emission wavelength ~530 nm is rhodamine 123 in homogeneous solution (methanol) with micromolar concentration. The sample used to measure the G-factor should be freely rotating in a single, uniform environment, ideally with monoexponential fluorescence decay kinetics. This will avoid artifacts arising from hindered rotations and associated anisotropy which can be found in complex samples [84]. This sample should also have similar spectral emission characteristics to the sample of interest. This is because the G-factor may vary as a function of wavelength due to differences in the spectral response of the detectors (see Note 1).
Select the objective you wish to use for the sample of interest and select/note the confocal pinhole size (see Note 2). Record the fluorescence decays with polarization parallel and perpendicular to the excitation beam with a suitable number of time channels in the decay (see Note 3). Where possible, ensure that the complete decay (into the noise floor) is recorded in the time window. This allows for the steady-state anisotropy to be correctly measured from the time-resolved data using the integrated decays in each detector (see Note 4). The photon count rate should be kept at around 1 % (or below) of the laser repetition rate to avoid photon pileup, both conventional pileup [85] and cross-detector pileup [86]. Ideally, these decays should be recorded simultaneously (using two detectors) to ensure that there are no artifacts due to sample or laser drift [87]. If the parallel and perpendicular decays are recorded sequentially using a single detector, then repeat measurements should be performed to ensure reproducibility.
Save the decays, and import into Origin (or similar spreadsheet/analysis software).
Subtract the background from each of the decays using the intensity values from the end of each decay trace, after the fluorescence has decayed completely, where the intensity value in each time channel should be only noise (see Note 5).
Perform any timing corrections necessary to ensure correct temporal overlap of the decays measured in each detector (see Note 6).
Divide the parallel signal by the perpendicular signal in each time channel. The limiting value of the resulting decay at long times is the G-factor—this is the tail-matching method. For an optimized system, this value will be close to 1.
Representative fluorescence decays of 3 μM rhodamine 123 in a 25/75 (V/V) methanol/glycerol mixture, yielding a G-factor of 1.15, are shown in Fig. 3a along with b the resulting fluorescence anisotropy decay curve.
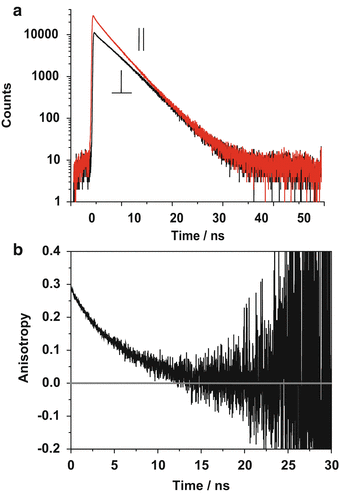

Fig. 3
Experimental arrangement for confocal microscope-based time-resolved anisotropy measurements. The sample is excited by linearly polarized pulsed laser light. The fluorescence polarized parallel and perpendicular to the incident light is separated using a polarizing beam splitter and detected using multichannel time-correlated single photon counting (TCSPC) [18]. The time- and polarization-resolved images are processed to give anisotropy images
3.3 Preparation and Measurement of Cell Samples
3.3.1 Living Cell Samples
Cells labeled with fluorescent proteins, quantum dots/nanoparticles, or stained with fluorescent dyes should be transferred to a suitable multi-well plate/sample chamber with a coverslide underside for imaging. This may be a micro-incubation system with a resistively heated multi-well plate with CO2 input (and medium exchange, if necessary) or dish or multi-well plate placed inside a specialized temperature-controlled housing around the microscope. The samples should be kept at 37 °C and 5 % CO2. The imaging medium should be free of fluorescent indicators (i.e., OptiMEM or equivalent) to eliminate measurement artifacts arising from the medium itself.
3.3.2 Fixed Cell Samples
Cells which have been fixed on microscope coverslides can be imaged at room temperature. Note that particularly thick samples such as tissue scatter and thus depolarize light.
3.3.3 Imaging the Cell Samples
Place samples on microscope stage and optimize CO2 levels/temperature as necessary.
Select an appropriate microscope objective for the measurements, making sure that the G-factor for the system is known for measurements using this objective. We typically use a 63× NA 1.2 water immersion objective (Leica) for living cell samples and a 63× NA 1.4 oil immersion objective (Leica) for fixed cell samples.
Obtain transmitted light and fluorescence images of the fluorescent cells, verifying that the fluorescence originates from the regions/organelles expected. Measure a fluorescence emission spectrum, from a series of wavelength-resolved images in order and verify that it corresponds to that of the dye or protein used in the cell labeling. These measurements, along with those from an unstained sample, will serve to check for and assess possible artifacts arising from autofluorescence. This procedure is not specific to polarization-resolved fluorescence experiments but is generally good practice.
Focus on the sample and select the region of interest (ROI) for imaging. If the ROI is found using software/hardware other than the B&H SPCM/SPC card (e.g., Leica software), then it is important to note that the image settings in SPCM will determine the region of the original image that will be imaged in the time-resolved measurements. Specifically, we typically image two 256 × 128 pixel images (one from each detector) using the B&H software with 256 time channels—a 256 × 256 pixel image would limit the maximum number of time channels to <256 available using the SPC-830 TCSPC card (see Note 7). (The measured 256 × 128 pixel image corresponds to the top half of the image recorded using the Leica confocal software).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


