and Jordan Smoller2
(1)
Department of Epidemiology, Albert Einstein College of Medicine, Bronx, NY, USA
(2)
Department of Psychiatry and Center for Human Genetic Research, Massachusetts General Hospital, Boston, MA, USA
Science is built up with facts, as a house is with stones. But a collection of facts is no more a science than a heap of stones is a house.
Jules Henri Poincare
La Science et l’Hypothese (1908)
1.1 The Logic of Scientific Reasoning
The whole point of science is to uncover the “truth.” How do we go about deciding something is true? We have two tools at our disposal to pursue scientific inquiry:
We have our senses, through which we experience the world and make observations.
We have the ability to reason, which enables us to make logical inferences.
In science we impose logic on those observations.
Clearly, we need both tools. All the logic in the world is not going to create an observation, and all the individual observations in the world won’t in themselves create a theory. There are two kinds of relationships between the scientific mind and the world and two kinds of logic we impose—deductive and inductive—as illustrated in Figure 1.1.
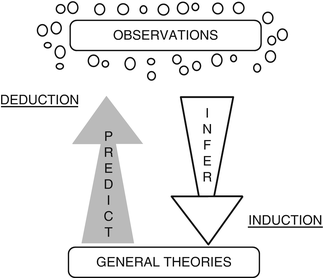

Figure 1.1
Deductive and inductive inference
In deductive inference, we hold a theory, and based on it, we make a prediction of its consequences. That is, we predict what the observations should be. For example, we may hold a theory of learning that says that positive reinforcement results in better learning than does punishment, that is, rewards work better than punishments. From this theory, we predict that math students who are praised for their right answers during the year will do better on the final exam than those who are punished for their wrong answers. We go from the general, the theory, to the specific, the observations. This is known as the hypothetico-deductive method.
In inductive inference, we go from the specific to the general. We make many observations, discern a pattern, make a generalization, and infer an explanation. For example, it was observed in the Vienna General Hospital in the 1840s that women giving birth were dying at a high rate of puerperal fever, a generalization that provoked terror in prospective mothers. It was a young doctor named Ignaz Phillip Semmelweis who connected the observation that medical students performing vaginal examinations did so directly after coming from the dissecting room, rarely washing their hands in between, with the observation that a colleague who accidentally cut his finger while dissecting a corpse died of a malady exactly like the one killing the mothers. He inferred the explanation that the cause of death was the introduction of cadaverous material into a wound. The practical consequence of that creative leap of the imagination was the elimination of puerperal fever as a scourge of childbirth by requiring that physicians wash their hands before doing a delivery! The ability to make such creative leaps from generalizations is the product of creative scientific minds.
Epidemiologists have generally been thought to use inductive inference. For example, several decades ago, it was noted that women seemed to get heart attacks about 10 years later than men did. A creative leap of the imagination led to the inference that it was women’s hormones that protected them until menopause. EUREKA! They deduced that if estrogen was good for women, it must be good for men and predicted that the observations would corroborate that deduction. A clinical trial was undertaken which gave men at high risk of heart attack estrogen in rather large doses, 2.5 mg per day or about four times the dosage currently used in postmenopausal women. Unsurprisingly, the men did not appreciate the side effects, but surprisingly to the investigators, the men in the estrogen group had higher coronary heart disease rates and mortality than those on placebo.2 What was good for the goose might not be so good for the gander. The trial was discontinued, and estrogen as a preventive measure was abandoned for several decades.
During that course of time, many prospective observational studies indicated that estrogen replacement given to postmenopausal women reduced the risk of heart disease by 30–50 %. These observations led to the inductive inference that postmenopausal hormone replacement is protective, i.e., observations led to theory. However, that theory must be tested in clinical trials. The first such trial of hormone replacement in women who already had heart disease, the Heart and Estrogen/progestin Replacement Study (HERS), found no difference in heart disease rates between the active treatment group and the placebo group, but did find an early increase in heart disease events in the first year of the study and a later benefit of hormones after about 2 years. Since this was a study in women with established heart disease, it was a secondary prevention trial and does not answer the question of whether women without known heart disease would benefit from long-term hormone replacement. That question has been addressed by the Women’s Health Initiative (WHI), which is described in a later section.
The point of the example is to illustrate how observations (that women get heart disease later than men) lead to theory (that hormones are protective), which predicts new observations (that there will be fewer heart attacks and deaths among those on hormones), which may strengthen the theory, until it is tested in a clinical trial which can either corroborate it or overthrow it and lead to a new theory, which then must be further tested to see if it better predicts new observations. So there is a constant interplay between inductive inference (based on observations) and deductive inference (based on theory), until we get closer and closer to the “truth.”
However, there is another point to this story. Theories don’t just leap out of facts. There must be some substrate out of which the theory leaps. Perhaps that substrate is another preceding theory that was found to be inadequate to explain these new observations and that theory, in turn, had replaced some previous theory. In any case, one aspect of the “substrate” is the “prepared mind” of the investigator. If the investigator is a cardiologist, for instance, he or she is trained to look at medical phenomena from a cardiology perspective and is knowledgeable about preceding theories and their strengths and flaws. If the cardiologist hadn’t had such training, he or she might not have seen the connection. Or, with different training, the investigator might leap to a different inference altogether. The epidemiologist must work in an interdisciplinary team to bring to bear various perspectives on a problem and to enlist minds “prepared” in different ways.
The question is, how well does a theory hold up in the face of new observations? When many studies provide affirmative evidence in favor of a theory, does that increase our belief in it? Affirmative evidence means more examples that are consistent with the theory. But to what degree does supportive evidence strengthen an assertion? Those who believe induction is the appropriate logic of science hold the view that affirmative evidence is what strengthens a theory.
Another approach is that of Karl Popper,1 perhaps one of the foremost theoreticians of science. Popper claims that induction arising from accumulation of affirmative evidence doesn’t strengthen a theory. Induction, after all, is based on our belief that the things unobserved will be like those observed or that the future will be like the past. For example, we see a lot of white swans and we make the assertion that all swans are white. This assertion is supported by many observations. Each time we see another white swan, we have more supportive evidence. But we cannot prove that all swans are white no matter how many white swans we see.
On the other hand, this assertion can be knocked down by the sighting of a single black swan. Now we would have to change our assertion to say that most swans are white and that there are some black swans. This assertion presumably is closer to the truth. In other words, we can refute the assertion with one example, but we can’t prove it with many. (The assertion that all swans are white is a descriptive generalization rather than a theory. A theory has a richer meaning that incorporates causal explanations and underlying mechanisms. Assertions, like those relating to the color of swans, may be components of a theory.)
According to Popper, the proper methodology is to posit a theory, or a conjecture, as he calls it, and try to demonstrate that it is false. The more such attempts at destruction it survives, the stronger is the evidence for it. The object is to devise ever more aggressive attempts to knock down the assertion and see if it still survives. If it does not survive an attempt at falsification, then the theory is discarded and replaced by another. He calls this the method of conjectures and refutations. The advance of science toward the “truth” comes about by discarding theories whose predictions are not confirmed by observations, or theories that are not testable altogether, rather than by shoring up theories with more examples of where they work. Useful scientific theories are potentially falsifiable.
Untestable theories are those where a variety of contradictory observations could each be consistent with the theory. For example, consider Freud’s psychoanalytic theory. The Oedipus complex theory says that a child is in love with the parent of the opposite sex. A boy desires his mother and wants to destroy his father. If we observe a man to say he loves his mother, that fits in with the theory. If we observe a man to say he hates his mother, that also fits in with the theory, which would say that it is “reaction formation” that leads him to deny his true feelings. In other words, no matter what the man says, it could not falsify the theory because it could be explained by it. Since no observation could potentially falsify the Oedipus theory, its position as a scientific theory could be questioned.
A third, and most reasonable, view is that the progress of science requires both inductive and deductive inference. A particular point of view provides a framework for observations, which lead to a theory that predicts new observations that modify the theory, which then leads to new, predicted observations, and so on toward the elusive “truth,” which we generally never reach. Asking which comes first, theory or observation, is like asking which comes first, the chicken or the egg.
In general then, advances in knowledge in the health field come about through constructing, testing, and modifying theories. Epidemiologists make inductive inferences to generalize from many observations, make creative leaps of the imagination to infer explanations and construct theories, and use deductive inferences to test those theories.
Theories, then, can be used to predict observations. But these observations will not always be exactly as we predict them, due to error and the inherent variability of natural phenomena. If the observations are widely different from our predictions, we will have to abandon or modify the theory. How do we test the extent of the discordance of our predictions based on theory from the reality of our observations? The test is a statistical or probabilistic test. It is the test of the null hypothesis, which is the cornerstone of statistical inference and will be discussed later. Some excellent classic writings on the logic and philosophy of science, and applications in epidemiology, are listed in the references section at the end of this book, and while some were written quite a while ago, they are still obtainable.2–7
1.2 Variability of Phenomena Requires Statistical Analysis
Statistics is a methodology with broad areas of application in science and industry as well as in medicine and in many other fields. A phenomenon may be principally based on a deterministic model. One example is Boyle’s law, which states that for a fixed volume an increase in temperature of a gas determines that there is an increase in pressure. Each time this law is tested, the same result occurs. The only variability lies in the error of measurement. Many phenomena in physics and chemistry are of such a nature.
Another type of model is a probabilistic model, which implies that various states of a phenomenon occur with certain probabilities. For instance, the distribution of intelligence is principally probabilistic, that is, given values of intelligence occur with a certain probability in the general population. In biology, psychology, or medicine, where phenomena are influenced by many factors that in themselves are variable and by other factors that are unidentifiable, the models are often probabilistic. In fact, as knowledge in physics has become more refined, it begins to appear that models formerly thought to be deterministic are probabilistic.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


