Fig. 1
Cross-section of the stent mesh, the coating, and the arterial wall: geometrical configuration and reference system (figure not to scale)
Our results demonstrate a strong coupling of the release kinetics in the polymer and the drug dynamics in the wall. The results highlight the importance of tailoring drug release to drug kinetics in the arterial wall to ensure optimal DES performance.
2 A Two-Layer Model for Drug Elution
We consider a stent that is coated with a thin layer (of thickness 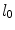 ) of a porous polymer containing a drug and that is embedded into the arterial wall. As the bulk of drug transport occurs along the direction normal to the polymeric surface (radial direction) and by assuming axial symmetry, we can restrict our study to a simplified one-dimensional model (Fig. 1). In particular, we consider a radial line crossing the metallic strut, the coating and the arterial wall and pointing outwards. Because the wall thickness is very small compared to the radius of the artery, a Cartesian coordinate system
) of a porous polymer containing a drug and that is embedded into the arterial wall. As the bulk of drug transport occurs along the direction normal to the polymeric surface (radial direction) and by assuming axial symmetry, we can restrict our study to a simplified one-dimensional model (Fig. 1). In particular, we consider a radial line crossing the metallic strut, the coating and the arterial wall and pointing outwards. Because the wall thickness is very small compared to the radius of the artery, a Cartesian coordinate system 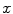 is used along the radial line. For simplicity, we consider the situation where the stent polymer is in direct contact with the medial layer of the arterial wall (hereafter simply referred to as wall). This layer is modeled as a homogeneous porous medium of thickness
is used along the radial line. For simplicity, we consider the situation where the stent polymer is in direct contact with the medial layer of the arterial wall (hereafter simply referred to as wall). This layer is modeled as a homogeneous porous medium of thickness 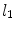 . Without loss of generality, we assume
. Without loss of generality, we assume 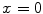 is the coating-wall interface (Fig. 1).
is the coating-wall interface (Fig. 1).
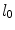 ) of a porous polymer containing a drug and that is embedded into the arterial wall. As the bulk of drug transport occurs along the direction normal to the polymeric surface (radial direction) and by assuming axial symmetry, we can restrict our study to a simplified one-dimensional model (Fig. 1). In particular, we consider a radial line crossing the metallic strut, the coating and the arterial wall and pointing outwards. Because the wall thickness is very small compared to the radius of the artery, a Cartesian coordinate system
) of a porous polymer containing a drug and that is embedded into the arterial wall. As the bulk of drug transport occurs along the direction normal to the polymeric surface (radial direction) and by assuming axial symmetry, we can restrict our study to a simplified one-dimensional model (Fig. 1). In particular, we consider a radial line crossing the metallic strut, the coating and the arterial wall and pointing outwards. Because the wall thickness is very small compared to the radius of the artery, a Cartesian coordinate system 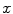 is used along the radial line. For simplicity, we consider the situation where the stent polymer is in direct contact with the medial layer of the arterial wall (hereafter simply referred to as wall). This layer is modeled as a homogeneous porous medium of thickness
is used along the radial line. For simplicity, we consider the situation where the stent polymer is in direct contact with the medial layer of the arterial wall (hereafter simply referred to as wall). This layer is modeled as a homogeneous porous medium of thickness 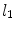 . Without loss of generality, we assume
. Without loss of generality, we assume 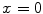 is the coating-wall interface (Fig. 1).
is the coating-wall interface (Fig. 1).In this paper we are interested in non-local mass transfer processes in the coating, where the drug passes from a solid (polymer-encapsulated, 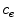 ) to a free phase (
) to a free phase (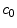 ) by dissolution. Similarly, a part of the dissolved and transported drug in the wall (
) by dissolution. Similarly, a part of the dissolved and transported drug in the wall (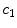 ) is metabolized by the cells and transformed to a bound state (
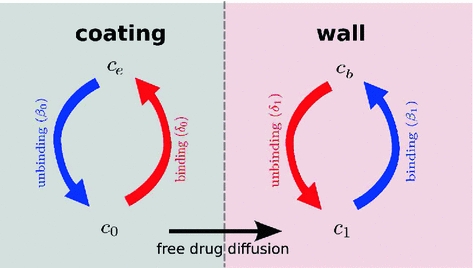
) is metabolized by the cells and transformed to a bound state (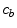 ). Thus, the drug delivery process starts in the coating and ends at the SMC receptors, with bidirectional phase changes in a cascaded sequence, as schematically depicted in Fig. 2. A microscopic approach would require knowledge of the specific and local geometry of the individual pore structure networks, which is unfeasible. Therefore, both the polymeric matrix and the wall are treated as macroscopically homogeneous porous media with volume-averaged concentrations. Even though we are only considering the 1D case in this study, we will express concentrations in units of
). Thus, the drug delivery process starts in the coating and ends at the SMC receptors, with bidirectional phase changes in a cascaded sequence, as schematically depicted in Fig. 2. A microscopic approach would require knowledge of the specific and local geometry of the individual pore structure networks, which is unfeasible. Therefore, both the polymeric matrix and the wall are treated as macroscopically homogeneous porous media with volume-averaged concentrations. Even though we are only considering the 1D case in this study, we will express concentrations in units of 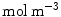 . These chosen units have no influence on the results.
. These chosen units have no influence on the results.
 ) to a free phase (
) to a free phase ( ) by dissolution. Similarly, a part of the dissolved and transported drug in the wall (
) by dissolution. Similarly, a part of the dissolved and transported drug in the wall (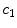 ) is metabolized by the cells and transformed to a bound state (
) is metabolized by the cells and transformed to a bound state (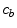 ). Thus, the drug delivery process starts in the coating and ends at the SMC receptors, with bidirectional phase changes in a cascaded sequence, as schematically depicted in Fig. 2. A microscopic approach would require knowledge of the specific and local geometry of the individual pore structure networks, which is unfeasible. Therefore, both the polymeric matrix and the wall are treated as macroscopically homogeneous porous media with volume-averaged concentrations. Even though we are only considering the 1D case in this study, we will express concentrations in units of
). Thus, the drug delivery process starts in the coating and ends at the SMC receptors, with bidirectional phase changes in a cascaded sequence, as schematically depicted in Fig. 2. A microscopic approach would require knowledge of the specific and local geometry of the individual pore structure networks, which is unfeasible. Therefore, both the polymeric matrix and the wall are treated as macroscopically homogeneous porous media with volume-averaged concentrations. Even though we are only considering the 1D case in this study, we will express concentrations in units of 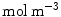 . These chosen units have no influence on the results.
. These chosen units have no influence on the results.
Fig. 2
Schematic of the cascade mechanism of drug delivery in the coating-wall coupled system. An unbinding (resp. binding) reaction occurs in the coating (resp. in the wall) (blue arrows). In both layers, reverse reactions (red arrows) are present in a dynamic equilibrium. Drug transport occurs only in the free phases 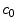 and
and 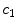
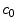 and
and 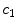
2.1 The Two-Phase Coating Model
The coating of a DES consists of a porous polymeric matrix that encapsulates a therapeutic drug in solid phase; as such, it is unable to diffuse and to be delivered into the tissue [5]. Nevertheless, when expanded and deployed into the wall, the stent coating is exposed to the surrounding biological fluids. As a consequence, such fluids fill the interstitial spaces of the polymer and form a network of liquid channels, acting as a release medium for the drug. Thus, a fraction of the drug mass is first transferred, in a finite time, to the liquid phase, and then released and diffuses into the arterial wall. We carry out a mesoscale description of the volume-averaged drug concentrations in the liquid (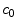 ) and solid (
) and solid (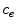 ) phases considered separately. By using a microstructure argument [17], the governing equations are:
) phases considered separately. By using a microstructure argument [17], the governing equations are:
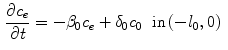
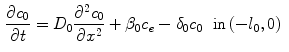
where 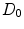 (
(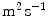 ) is the diffusion coefficient of the unbound solute,
) is the diffusion coefficient of the unbound solute, 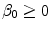 (
(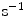 ) and
) and 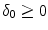 (
(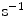 ) are the unbinding (dissociation) and binding (re-association) rate constants in the coating, respectively [10]. It should be noted that
) are the unbinding (dissociation) and binding (re-association) rate constants in the coating, respectively [10]. It should be noted that 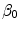 depends on the porosity of the coating
depends on the porosity of the coating 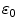 [17]. The binding rate constant is defined as the inverse of the characteristic solid-liquid transfer time scale,
[17]. The binding rate constant is defined as the inverse of the characteristic solid-liquid transfer time scale, 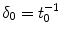 . The ratio of the unbinding and binding rate constants is the equilibrium dissociation constant
. The ratio of the unbinding and binding rate constants is the equilibrium dissociation constant 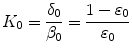 .
. 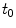 and
and 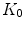 are quantities that can typically be determined experimentally.
are quantities that can typically be determined experimentally.
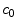 ) and solid (
) and solid (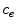 ) phases considered separately. By using a microstructure argument [17], the governing equations are:
) phases considered separately. By using a microstructure argument [17], the governing equations are: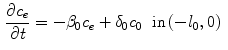
(1)
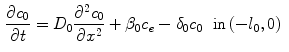
(2)
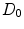 (
(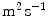 ) is the diffusion coefficient of the unbound solute,
) is the diffusion coefficient of the unbound solute, 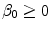 (
(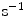 ) and
) and 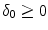 (
(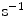 ) are the unbinding (dissociation) and binding (re-association) rate constants in the coating, respectively [10]. It should be noted that
) are the unbinding (dissociation) and binding (re-association) rate constants in the coating, respectively [10]. It should be noted that 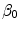 depends on the porosity of the coating
depends on the porosity of the coating 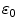 [17]. The binding rate constant is defined as the inverse of the characteristic solid-liquid transfer time scale,
[17]. The binding rate constant is defined as the inverse of the characteristic solid-liquid transfer time scale, 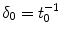 . The ratio of the unbinding and binding rate constants is the equilibrium dissociation constant
. The ratio of the unbinding and binding rate constants is the equilibrium dissociation constant 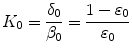 .
. 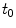 and
and 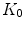 are quantities that can typically be determined experimentally.
are quantities that can typically be determined experimentally.The associated initial conditions are:

expressing that, at initial time, the entire drug exists in the solid phase at a maximum constant concentration, and it is subsequently released into the liquid phase. Since the metallic strut is impermeable to the drug, no mass flux passes through the boundary surface 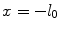 ; hence, we impose a no-flux condition:
; hence, we impose a no-flux condition:


(3)
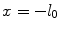 ; hence, we impose a no-flux condition:
; hence, we impose a no-flux condition:
(4)
2.2 The Two-Phase Wall Model
Drug that enters the arterial wall is transported by convection and diffusion through the tortuous paths of the extracellular matrix surrounding the wall’s cells. Similarly to the coating, a phase change can occur in the wall from the free state (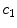 ) of the drug to the bound state (
) of the drug to the bound state (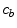 ) and vice versa at the surface of the cells within the wall. The free drug (
) and vice versa at the surface of the cells within the wall. The free drug (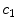 ) binds to specific receptors on the surface of SMCs to form a bound complex (
) binds to specific receptors on the surface of SMCs to form a bound complex (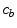 ). The maximum density of specific receptors available to the drug is denoted as
). The maximum density of specific receptors available to the drug is denoted as 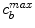 . The formed drug-receptor complex is not permanent and can be dissolved after a typical time scale
. The formed drug-receptor complex is not permanent and can be dissolved after a typical time scale 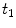 . These two processes (binding and unbinding) are modeled by a second order reversible saturating binding equations [1]:
. These two processes (binding and unbinding) are modeled by a second order reversible saturating binding equations [1]:
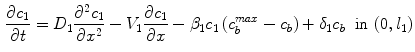
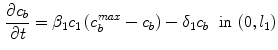
where 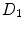 is the effective diffusivity of unbound drug,
is the effective diffusivity of unbound drug, 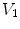 (
(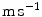 ) is a convection velocity, and
) is a convection velocity, and 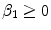 (
(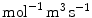 ) and
) and 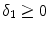 (
(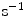 ) are the binding and unbinding rate constants, respectively [15]. The unbinding rate constant is defined by the inverse of the characteristic unbinding time scale,
) are the binding and unbinding rate constants, respectively [15]. The unbinding rate constant is defined by the inverse of the characteristic unbinding time scale, 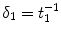 . It should be noted that due to the cross product of
. It should be noted that due to the cross product of 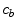 and
and 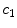 in the binding term of Eq. (6), the units of
in the binding term of Eq. (6), the units of 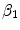 are different from those of
are different from those of 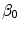 (
(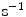 ).
). 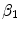 is related to
is related to 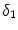 by the equilibrium dissociation constant
by the equilibrium dissociation constant 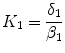 (
(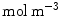 ). The initial conditions are:
). The initial conditions are:

Finally, a perfectly absorbing boundary condition is imposed at the wall limit:

At the coating-wall interface, we impose the balance of flux
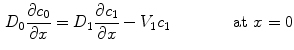
and continuity of the liquid-phase concentration:
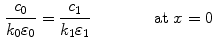
where 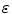 and
and 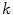 are the porosities and the partition coefficients in the respective layers.
are the porosities and the partition coefficients in the respective layers.
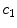 ) of the drug to the bound state (
) of the drug to the bound state (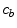 ) and vice versa at the surface of the cells within the wall. The free drug (
) and vice versa at the surface of the cells within the wall. The free drug (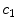 ) binds to specific receptors on the surface of SMCs to form a bound complex (
) binds to specific receptors on the surface of SMCs to form a bound complex (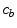 ). The maximum density of specific receptors available to the drug is denoted as
). The maximum density of specific receptors available to the drug is denoted as 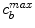 . The formed drug-receptor complex is not permanent and can be dissolved after a typical time scale
. The formed drug-receptor complex is not permanent and can be dissolved after a typical time scale 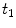 . These two processes (binding and unbinding) are modeled by a second order reversible saturating binding equations [1]:
. These two processes (binding and unbinding) are modeled by a second order reversible saturating binding equations [1]: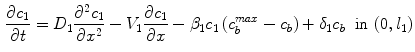
(5)
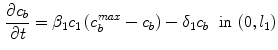
(6)
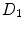 is the effective diffusivity of unbound drug,
is the effective diffusivity of unbound drug, 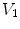 (
(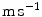 ) is a convection velocity, and
) is a convection velocity, and 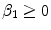 (
(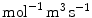 ) and
) and 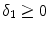 (
(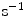 ) are the binding and unbinding rate constants, respectively [15]. The unbinding rate constant is defined by the inverse of the characteristic unbinding time scale,
) are the binding and unbinding rate constants, respectively [15]. The unbinding rate constant is defined by the inverse of the characteristic unbinding time scale, 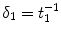 . It should be noted that due to the cross product of
. It should be noted that due to the cross product of 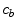 and
and 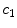 in the binding term of Eq. (6), the units of
in the binding term of Eq. (6), the units of 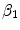 are different from those of
are different from those of 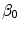 (
(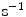 ).
). 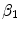 is related to
is related to 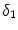 by the equilibrium dissociation constant
by the equilibrium dissociation constant 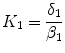 (
(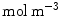 ). The initial conditions are:
). The initial conditions are:
(7)

(8)
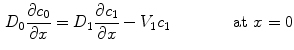
(9)
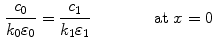
(10)
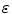 and
and 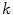 are the porosities and the partition coefficients in the respective layers.
are the porosities and the partition coefficients in the respective layers.2.3 Physiological Parameters
The two most common drugs used for DES are paclitaxel and sirolimus. These two drugs have similar molecular size and resulting transport properties (effective diffusivity and convection velocity), but drastically different binding and unbinding dynamics in the arterial wall, resulting in different binding 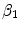 and unbinding
and unbinding 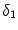 rate constants and maximum binding site densities
rate constants and maximum binding site densities 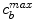 [14]. Based on the parameters determined in [14, 15, 17], we have chosen a set of parameters that describes a generic drug that is similar in its transport properties to paclitaxel and sirolimus and lies in between paclitaxel and sirolimus for its binding/unbinding properties. The parameters of the reference model are summarized in Table 1. We consider the entire polymer and wall tissue as accessible and thus
[14]. Based on the parameters determined in [14, 15, 17], we have chosen a set of parameters that describes a generic drug that is similar in its transport properties to paclitaxel and sirolimus and lies in between paclitaxel and sirolimus for its binding/unbinding properties. The parameters of the reference model are summarized in Table 1. We consider the entire polymer and wall tissue as accessible and thus 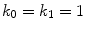 . The values for
. The values for 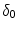 and
and 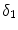 correspond to a characteristic solid-liquid transfer time
correspond to a characteristic solid-liquid transfer time 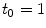 day and an unbinding time scale
day and an unbinding time scale 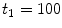 h, respectively.
h, respectively.
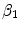 and unbinding
and unbinding 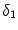 rate constants and maximum binding site densities
rate constants and maximum binding site densities 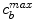 [14]. Based on the parameters determined in [14, 15, 17], we have chosen a set of parameters that describes a generic drug that is similar in its transport properties to paclitaxel and sirolimus and lies in between paclitaxel and sirolimus for its binding/unbinding properties. The parameters of the reference model are summarized in Table 1. We consider the entire polymer and wall tissue as accessible and thus
[14]. Based on the parameters determined in [14, 15, 17], we have chosen a set of parameters that describes a generic drug that is similar in its transport properties to paclitaxel and sirolimus and lies in between paclitaxel and sirolimus for its binding/unbinding properties. The parameters of the reference model are summarized in Table 1. We consider the entire polymer and wall tissue as accessible and thus 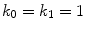 . The values for
. The values for 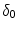 and
and 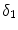 correspond to a characteristic solid-liquid transfer time
correspond to a characteristic solid-liquid transfer time 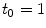 day and an unbinding time scale
day and an unbinding time scale 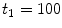 h, respectively.
h, respectively.Table 1




Model parameters of the reference model
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


