Fig. 1
TIRF versus epifluorescence imaging. A fixed MDA-MB-231 breast cancer cell labeled for alpha-tubulin (a, b) and phospho-paxillin (c, d). TIRF imaging (a, c) results in a much higher signal-to-noise ratio for both structures compared to epifluorescence imaging (b, d) which has a hazy appearance. Scale bar: 10 μm. (g, h) Show the illumination schematics for TIRF (g) and epifluorescence (h)
Although there now exists numerous commercially available TIRF systems, there are still several considerations that need to be taken into account before purchasing a system to ensure that you meet the requirements of your experiment and achieve the desired image quality.
Most commercially available TIRF microscopes use a “through-the-objective” optical configuration (we describe this and its alternative below). One of the most important considerations for this type of setup is the choice of the objective lens used. High numerical aperture (NA) lenses are always desirable for high-resolution optical microscopy, as they ultimately determine the “resolving power” of a system due to Abbe theory of imaging [19]. It is generally agreed in the literature that the physical minimum for an objective-based TIRF setup is 1.40 NA, but in practice, 1.45 NA is usually the smallest used. The reasons for this are described in detail in the “objective-based TIRF” section. Usually the cost of an objective lens increases with the numerical aperture (NA) of the lens. Therefore, choosing the correct objective for your application, while considering cost implications, is a significant factor when designing your TIRF system.
Another import element that will affect the image quality is the type of camera chosen. Factors influencing camera performance are described in detail in Millis [20], but the main points are summarized here. Monochromatic charge-coupled devices (CCDs) are generally preferable over color-based CCDs. Cameras come with different bit depths; a higher bit depth means that a greater number of gray levels can be detected, increasing dynamic range of intensity measured. For example, a 12-bit camera in our system gives 212 = 4,096 gray levels. If imaging speed is an important factor in your research, an electron-multiplying CCD (EM-CCD) may be more appropriate. EM-CCDs are much more sensitive to low light and therefore allow exposure times to be reduced, allowing faster imaging and also reducing photobleaching of the sample. The physical pixel size of EM-CCDs is typically larger than those in standard CCDs, and hence, the resolution of the resulting images is lower. To compensate for this, higher magnification objectives, e.g., 150×, may have to be used to ensure that optical images are sampled above the Nyquist criteria. EM-CCDs are also very expensive and are easily damaged by relatively intense light signals or prolonged low-intensity light signals.
Many applications of TIRF require imaging of more than one color, for example, imaging dynamics of a receptor where the receptor (EGFR) is labeled in green and a vesicle marker (clathrin) is in red [21]. In many other instances, simultaneous acquisition of the two colors would be beneficial as a lot of processes occur very rapidly and switching between different wavelengths might mean that any colocalization may not be detected, when it really does occur. If rapid imaging of two color samples is necessary for your application, it may be worth investing in an emission beam splitter that allows simultaneous imaging of the two colors. This separates the emitted light into two separate beams (one per color) that are each projected onto one half of the camera chip. Although the two colors are imaged simultaneously, there is the drawback that the area that can be imaged is half of that which can be obtained via sequential imaging. Therefore, whether to perform simultaneous or sequential two-color imaging will depend on what is more important to your application.
Once you have your system up and running, the next thing you need to think about is the design of your experiments. Although it is true that an image is worth a thousand words, a TIRF image of a cell without proper quantitative analysis is just a pretty picture. When planning experiments, it is necessary to think about ways to get the most data out of your image and to ensure that you really are measuring the processes that you want to study. In this chapter, we will briefly outline the physical basis of TIRF microscopy, describing the two main different optical configurations, prism- and objective-based, and also introduce another specialist TIRF technique called variable angle TIRF microscopy (VA-TIRFM). We will discuss the benefits of combining TIRF with other microscope modalities and then delve into some of the biological applications of TIRF microscopy and include important tips and tricks for setting up experiments and analyzing the imaging data.
1.1 The Physical Basis of TIRF
Every advantage of using TIRF microscopy emanates from the physical properties of the illumination method that it employs. Therefore, an understanding of the fundamental physical principles behind the formation of TIRF images is absolutely necessary to reap the full benefits of this powerful microscopy technique. This knowledge is also essential when trying to interpret and extract quantitative information from the images obtained through TIRF, as factors such as fluorophore position within the illumination field have a significant influence on the apparent intensity of its fluorescence. This section aims to provide the reader with some of the key physical concepts behind TIRF microscopy as well as important considerations for choosing the appropriate TIRF configuration for various biological applications.
TIRF microscopy relies on what is known as an evanescent field, which serves to exclusively illuminate a thin plane just above the imaging surface, i.e., a glass coverslip. The evanescent field is produced when light rays are totally internally reflected at the interface between the imaging surface and an aqueous medium. Below is a short explanation of the fundamentals of total internal reflection for dielectric media (media that does not conduct electricity; most applications of TIRF in cell biology use dielectric media).
The refractive index, n, of an optical medium tells us how electromagnetic waves, in this case visible light, propagate through it, relative to how it propagates through a perfect vacuum. It is defined as n = c/v, where c is the velocity of light in a vacuum and v the velocity of light in the medium. When light rays propagating through one medium (e.g., glass) meet an interface of another medium (e.g., air, water, cytosol) which has a different refractive index, the subsequent direction of the light rays is changed depending on the angle at which the light meets this interface (Fig. 2). Some of the light rays may be reflected from the interface and some may be transmitted into the second medium (Fig. 2a). If the refractive indices of both media are known, n 1 and n 2, as well as the angle of incidence, θ 1, then Snell’s law gives us the angle at which light rays are transmitted and/or reflected from this interface, θ 2 Eq. 1.
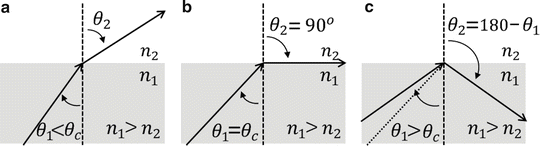
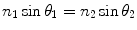
Total internal reflection occurs when the refractive index of the first medium is greater than that of the second, n 1 > n 2, and the angle of incidence is greater than what is known as the “critical” angle, θ c. When the angle of incidence is equal to the critical angle, θ 1 = θ c, light rays emerge into the second medium and propagate tangentially along the direction of the interface, or θ 2 = 90° (Fig. 2b). So Snell’s law gives us: n 1 sin θ c = n 2 sin 90°, sin 90° = 1, and therefore, θ c = sin− 1(n 2/n 1). For angles of incidence greater than θ c, light rays are totally reflected back into the first medium (Fig. 2c).

Fig. 2
Ray diagrams for the case of total internal reflection. This figure shows how the direction of light rays changes when they propagate through one medium (gray ) and encounter an interface of a second medium (white ), such that they experience an abrupt decrease in refractive index. (a) The angle of incidence is less than the critical angle. (b) The angle of incidence is equal to the critical angle. (c) The angle of incidence is greater than the critical angle
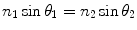
(1)
As we have just seen, Snell’s law describes which direction light rays leave a boundary between two media for a given angle of incidence, but it tells us nothing about the proportions of the light reflected and transmitted from such a boundary; Fresnel’s equations must be used in for this. When Fresnel’s equations are solved for the case of total internal reflection, they show that although the propagation of the light rays is totally reflected, there is still an electric component of light which crosses the boundary and, hence, still a field in the second medium. This field is known as the evanescent field, and its intensity decays exponentially with perpendicular distance from the boundary:
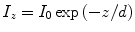
where I z is the field intensity at the distance, z, from the interface, d is the decay constant of the field, and I 0 is the intensity of the field at the interface (z = 0).
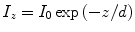
(2)
The mathematics behind this is beyond the scope for this article, but interested readers are referred to texts [19, 22] or other good optics text books. In addition, Fresnel’s equations demonstrate that there are also implications for the amplitude of an evanescent field for different polarizations of the incident light [2]. However, apart from some specialist experiments [23, 24], the effects of polarization are negligible.
1.2 Penetration Depth
The penetration depth of the evanescent field for a particular TIRF configuration is critical. Local areas of high refractive index within a sample will convert the evanescent field into scattered propagating light which will in turn contaminate images. For that reason, it is often desirable for a TIRF system to have the capability to vary the penetration depth of the evanescent field. The equation below shows what determines the penetration depth of the evanescent field:
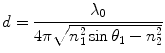
This is perhaps one of the most important equations when designing TIRF-based experiments as there are severe technical/economic implications on the ability to adjust the penetration depth. It shows that the penetration depth is dependent on the wavelength of the excitation beam, λ 0; the angle of incidence of the excitation beam, θ 1; and the refractive indices of the two media: n 1 and n 2. In practice, we do not usually have much control on the refractive index of a biological sample (n 2), and we are usually confined to specific excitation wavelengths (λ 0) of a specific fluorophore once in a sample. We cannot vary the refractive index of the imaging surface once intact during an experiment (n 1). Therefore, experimentally we can only control the penetration depth through variation of the angle of incidence. However, as described below, with many commercially available TIRF objectives, the ability to vary the angle of incident light and thus penetration depth can be limited.
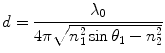
(3)
1.3 TIRF Configurations
When TIRF microscopy was first applied in the field of cell biology, the experimental setup consisted of a few basic components added to an inverted fluorescence microscope [25]. Since then, many different optical configurations have been designed and presented in publications, most of which fall into two categories, either prism-based or through-the-objective-based TIRF systems.
1.3.1 Prism-Based TIRF
The key to producing an evanescent field at the imaging surface/sample interface is the delivery of light rays to the interface at the correct angle of incidence. In order to get a “pure” evanescent field, all light rays must meet the interface with the same angle of incidence. A pure evanescent field is one which follows a single exponential profile Eq. 2 with a given decay constant, d. If the incident beam of light meets the interface with a spread of angles, then a field consisting of multiple evanescent fields is created, each with different penetration depths; thus, we no longer follow the profile of a single exponential. Therefore, the excitation beams must be well collimated, and the imaging surface should be as flat as possible. With the aim of imaging cell substrates, glass prisms were optically coupled to glass coverslips, to which cells were adhered, to ensure that these two conditions were met. Hence, the origin of the term “prism-based” TIRF. There are several different configurations for prism-based TIRF microscopes, the first introduced into cell biology studies by Axelrod in 1981 [25].
Although through-the-objective systems are becoming increasingly popular, there are numerous benefits of using prism-based systems. Some of these benefits include:
1.
Prism-based systems are typically cost-effective as they can be constructed with “off-the-shelf” components and “home built” in a laboratory/department workshop. Thus, they are not confined to any particular manufacturer or microscope system.
2.
They usually achieve a “purer” evanescent field due to the fact that it is easy to get well-collimated light to the reflective boundary (i.e., minimal scattered light).
3.
The resultant evanescent field covers the full field of view, again due to ease of focusing collimated light to the sample interface.
4.
Prism-based systems can be designed and built to suit a specific purpose.
Some of the main disadvantages of prism-based systems include:
1.
It is difficult to change the angle of incidence (although for simple prism-based setups, a variable angle design is demonstrated in Stock et al. [26]).
2.
It is more complicated to set up each experiment as they require the imaging surface (typically a glass coverslip) to be optically coupled to the prism using substances such as glycerol.
1.3.2 Objective-Based TIRF
As the potential of TIRF was realized, and its use in cellular imaging increased, various developments were made to the technology which led to the design of the “through-the-objective”-based systems. The main advantage of this design is that the excitation light is delivered by the objective lens like most other microscopy modalities, therefore making it easier to perform experiments on a high-throughput basis.
The excitation beam is directed off-axis in the back focal plane of the objective and along the periphery of a high NA lens such that it emerges from the front aperture at a sufficiently high angle to achieve total internal reflection at the coverslip/sample interface. In objective-based TIRF systems, high NA objectives are a necessity because of the high angle of incidences required for achieving total internal reflection at the coverslip/sample interface. High NA provides the freedom of a larger range of incident angles and hence variation of penetration depth; therefore, most commercially available lenses are 1.45 and 1.49, but higher NA lenses are available. Olympus has a 100×, 1.65 NA objective which is capable of producing a very pure evanescent field at low penetration depths. The drawback of this lens is that it requires a special immersion oil (which is volatile) and expensive sapphire high refractive index coverslips to match. Fish’s review has a good discussion on the NA of an objective and the range of above critical angles [27].
As stated above, in order to get a “pure” evanescent field, the incident light rays need to all meet the coverslip/sample interface at the same angle of incidence. The challenge with the objective-based systems is maintaining a well-collimated beam of light through the special confinements of the margins of the objective lens.
There are many advantages of using an objective-based TIRF system, including:
1.
It is easier to use than a prism-based system as it is not restricted by the position of a prism in the setup and does not require the imaging surface to be optically coupled to a prism with a liquid such as glycerol.
2.
The user is free to use different off-the-shelf imaging surfaces, i.e., microscope slides, coverslips, and glass-bottom dishes, providing that they have an appropriate refractive index.
3.
Light paths can be changed at a “flick of a switch” to image with different wavelengths or imaging modalities.
4.
Useful for multipoint, multi-dish, or slide experiments as the excitation and emission beams come from the same side of the objective.
Essentially, all commercially available TIRF microscopes employ objective-based TIRF. These generally allow rapid change of TIRF angle and switching between excitation beams. Some even have simultaneous dual-wavelength or multiwavelength imaging capability by exciting with two or more different wavelengths at the same time and chromatically separating the light emitted from the sample using a beam splitter. Simultaneous wavelength can be achieved in two ways: (1) Use a beam splitter combined with a right-angle prism, so that the separated light paths are projected in adjacent positions on the same CCD chip. (2) A separate CCD could be used for each light path coming from the beam splitter. The former has the obvious disadvantage of sacrificing the field of view for each channel, and the latter is considerably more expansive as it requires additional cameras.
Although through-objective TIRF systems do offer many advantages over the prism-based setups, there are also a few disadvantages:
1.
The evanescent waves produced by the through-the-objective-based systems are usually less “pure” than prism-based systems. This is because more rays are scattered as the excitation beam is guided through the back focal plane of the objective than in the prism-based systems.
2.
Due to the obscure path the light has to take to leave the objective at the correct angle, the resultant diameter of the beam leaving the objective is very small, typically smaller than the field of view of the microscope. Consequently, the width of the evanescent field is also less than the field of view of the microscope, and hence the image intensity is seen to drop off at the edges of images.
3.
The maximum angle of incidence achievable with through-the-objective systems is restricted by the NA of the objective, and therefore, smaller penetration depths are achievable with prism-based systems.
4.
Purpose-built TIRF objectives are specially engineered so typically cost several thousand pounds.
1.3.3 Variable Angle TIRF Microscopy (VA-TIRFM)
Earlier we discussed the factors that influence the penetration depth of the evanescent field and gave the equation which relates them. We also point out that the only one of these we have any real control over during an experiment is the angle of incidence of the laser beam. Altering this gives us control of the penetration depth of the evanescent field providing the option of illuminating as deep or as shallow into the sample as we wish (Fig. 3), within the constraints of the system (realistically between 100 and 400 nm although 60–600 nm is theoretically possible depending on the specific setup). The technique of VA-TIRF makes possible the measurement of submicroscopic z-distances, with slices up to 10 times thinner than those achieved with a confocal scanning microscope. This allows a much finer level of detail to be resolved in in vitro studies, for example, determining distances between fluorescent probes and cell membranes [28] or the ability to map cell-substrate topology [26]. There are several ways to implement such a technique. The most common models incorporate a single or series of rotating mirrors [26, 28], though setups with an acousto-optic modulator and telecentric lens optics with wavelength-dependant deflection angles and varying image planes are also relatively common [29, 30]. As long as the optics contain a correction for movement of the exciting laser beam in the x – y plane when the angle of incidence is changed, then variable angle TIRF is possible on nearly any system.
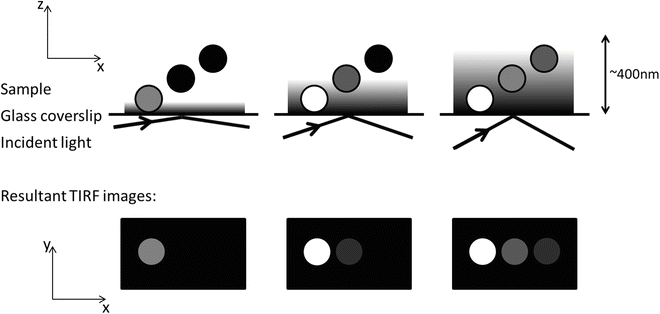

Fig. 3
Variable Angle TIRF. This figure shows how the penetration depth of the evanescent wave varies with incident angle of the incoming laser. The resultant images are shown beneath
Images obtained through this method can be interpreted in a number of different ways. In cell biological applications, qualitative measurements, when the detection of membrane-bound fluorophores is differentiated from those located in the cytosol alone, are possible as are quantitative observations based on relative levels of fluorophore excitation [31]. As of yet, we are not aware of reports of a 3D image stack being created from the images, but the theoretical framework is there.
1.4 TIRF and Other Microscopy Techniques Combined
1.4.1 Epi–TIRF
The addition of a TIRF system to a microscope leaves its optical configuration relatively unchanged; therefore, the sample is still accessible by other microscopy light paths. Most commonly, TIRF is combined with epifluorescence microscopy, due to the fact that they are both widefield techniques and use the same collection optics (filters, dichroics, CCD cameras) which makes it easy to switch between them. Epi-illumination can be achieved in one of the following two ways: (1) through use of an independent epi-light source such as a standard arc lamp light source and (2) by changing the angle of incidence from above the critical angle for TIRF to a subcritical angle such that light is no longer reflected and hence propagates into the sample. The former method is the one more commonly seen in the literature [32–34] as the mechanical switching between each excitation light path can be performed very rapidly (typically a hundreds of milliseconds, some as fast as tens of milliseconds). The latter is less popular due to the speed at which most TIRF systems can “detune” the TIRF beam and then accurately “tune” it again. However, now commercially available microscopes are being produced which can rapidly and accurately change the angle of incidence of the excitation beam for this purpose.
1.4.2 Confocal–TIRF
Combining TIRF with epifluorescence has its obvious limitations, the main being the large depth field of the epi-illumination. In order to overcome this limitation, it can be combined with confocal microscopy because of its optical sectioning capability. Images from confocal microscopes represent a much thinner cross section than epifluorescence images (~1μm compared to ~10μm) because the effective volume of the point spread function (PSF) of confocal is much smaller than that of epi. In conjunction with the sharp PSF, a pin hole is placed before the detector which prevents out-of-focus light rays from reaching the detector. Conventional point-scanning confocal microscopes use a pair of oscillating mirrors to scan the focal point of the excitation light across planar sections through the sample. Any fluorescence from the focal point is then detected using a photon multiplier tube, converted to a digital signal, and the image is recorded serially by a computer. Because images are constructed in this point-by-point manner, the acquisition time per image can be significantly greater than that of the CCD-based acquisition of epi or TIRF (e.g., ~1 s compared to ~100 ms for a 1,000 × 1,000 pixel image). As a result, it would not be possible to perform some of the same experiments which combine epi with TIRF as the distribution of fluorophores within the evanescent field can change significantly in the time it takes to acquire a confocal image. To overcome this limitation, fast confocal systems such as a resonance scanner or spinning disk configurations can be used which are capable of acquiring a 512 × 512 two-dimensional image in ~100 ms (some spinning disk systems can acquire images in less than 20 ms). Resonance scanner systems use high-temporal-resolution photon multiplier tubes and form images in the same way conventional confocal microscopes do. To facilitate colocalization studies with TIRF and resonance scanner images, their data sets must be co-registered as they will generally differ by a rotation, scale, and position within the image. A method for automated co-registration is presented in Pitkeathly et al. [35].
Spinning disk confocal microscopes use an array of micro lenses on a fast rotating disk which is used to simultaneously illuminate multiple points in the sample rather than scanning a single point across it. Images are recorded using a high-grade CCD, and in some setups, the TIRF images are acquired with the same CCD. If the same CCD is used for both light paths, then the images should already be naturally registered. However, this configuration will potentially require significant switch times to alter the light paths.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


