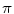(1)
University of South Australia, Adelaide, Australia
Abstract
This chapter presents “The pharmacotherapy needs a premium” Game where the Institution that lowers the decision threshold must respond to the industry’s Threat. The pharmaceutical industry’s claim is that while the health shadow price β c captures information about the budget constraint and can improve static efficiency in a fixed budget, β c does not capture information about the loss in future health as a consequence of lower drug prices today. The industry claims that new drugs should have a premium above the threshold for other programmes because when a fund holder buys new drugs they are also buying future innovation. The Game is structured as a Firm’s choice between two strategies: (1) invest in research and development; or (2) do nothing. The Game extends over three periods and up to two drugs (a new drug and a future drug) can be developed. The key decision by the Institution is whether or not to pay a premium over β c for the new drug (the first drug) in order to facilitate development of the future (second) drug. The result of the Game is that there is no incentive for an Institution to price above β c for the new drug in order to generate an incentive for the Firm to develop the future drug. Furthermore, pricing above β c is found to be neither a necessary nor sufficient condition for the development of the future drug. I conclude that the Institution should respond to the Threat by suggesting that the Firm approach the Capital Market and that this is the social-welfare-maximising solution.
10.1 The Reimburser’s Problem
The Reimburser is presented with a new drug by a pharmaceutical Firm. The new drug is more effective than the best existing drug, ΔE P > 0 but it also comes at an additional financial cost, ΔC P > 0. In order to finance the new drug within the fixed economically efficient health budget, an existing programme needs to be displaced; the least cost-effective of existing programmes. However, this existing programme has an aICER less than the IPER of the new drug (m < f), therefore, the health effects displaced to finance the new drug will be more than the health effects gained from reimbursing the new drug. Furthermore, the budget is currently economically efficient and displacement is optimal so, using PEA, the threshold is β c = d = m, where d is the aICER of an optimally displaced service and m is the aICER of the least cost-effective in contraction of an existing programme.
The Reimburser is reluctant to choose to reimburse the new drug in this situation. However, the Firm presents the Reimburser with a paper by pharma-economists Jena and Philipson (2008) who propose that new pharmaceuticals should have a higher threshold applied to them than non-pharmaceutical inputs. The authors’ reasoning is that purchasing the former is simply buying health effects from current technologies whereas purchasing new drugs has the benefits of both current health effects and future innovation. They claim that the product with the worst cost-effectiveness could also be the one that maximises health and status and dynamic efficiency. They suggest that the choice is not between “a cheap or expensive technologies once marketed—as CE adoption suggests.”1 Instead the choice is one between an “initially expensive technology and no technology” and if the latter is chosen then society is also choosing a future with “higher real prices for producing a healthy life” (Jena and Philipson 2008, p. 1235).
The Reimburser recognises that the programme that will be displaced to finance the additional costs of the new drug does not have an R&D component, so there appears to be little potential to change the efficiency of future health budgets through improved technology via this programme. Jena and Philipson’s conclusion has intuitive appeal: why not pay a bit extra for a new drug, given that we are getting more than just the health effects of that drug? The Reimburser asks her Health Economic Adviser how the Institution should respond to the following Threat.
When the Institution buys this new drug, it buys the health effects from this drug and the health benefits from future innovation. This is not the case with other health programmes. Therefore, unless the Institution pays a premium for the health effects from the new drug, the population will be worse off because innovation will be suboptimal and the future drug will not be produced.
10.2 The Pharmacotherapy Needs a Premium Game
Chapter 8 presented a one-period GTM of the reimbursement process. The following Game extends that one-period model to a three-period model where the decisions linking successive time periods are the Firm’s decision to invest today in the R&D required for future drugs and the Reimburser’s decision to change the threshold price in order to change the availability of future NMEs.
This game is set out in the following four Sects. (10.3 to 10.6). Section 10.3 describes the World from which the problem characterised by the same is drawn. In Sect. 10.4 the model is described and defined, first in terms of the Narrative then the structure of the applied game. The theory used to derive the solution is described in Sect. 10.5 and the Solution is presented in Sect. 10.6.
10.3 The World
In 2008 a Firm developed a new drug, Araamax for rheumatoid arthritis. The evidence from double-blinded RCTs showed a statistically and clinically significant gain to a subgroup of patients compared with the existing best therapy, Rathmab. Purchasing Araamax will come at a significant additional cost to the health care sector, ΔC P , which will be financed by displacing an existing programme. The aICER of the displaced programme is less than the IPER of the new drug so there will be a net loss in the population’s health. However, the Firm claims that because the new drug has both dynamic and static welfare implications whereas the existing programme has only the latter, the new drug should be purchased at the offer price despite the short-term reduction in the health effects for the population.2
The Firm makes the following Threat.
When the Institution buys this new drug, it buys the health effects from this drug and the health benefits from future innovation. This is not the case with other health programmes. Therefore, unless the Institution pays a premium for the health effects from the new drug, the population will be worse off because innovation will be suboptimal and the future drug will not be produced.
How should the Institution respond to this Threat?
10.4 The Model
The Model comprises the Narrative and the Game Structure.
10.4.1 The Narrative
The Game takes place over three periods. Currently patients with rheumatoid arthritis use a drug called Rathmab which is off-patent and hence its IPER, compared with placebo, is the same as its IMER; there is no economic rent. It is produced by a different firm from the one in this Game.
Note
The relationship between the IMER, IPER and IπER of each of the three drugs is illustrated using numeric values for variables in Tables 10.1, 10.2, 10.3, 10.4 and 10.5. The Game is solved algebraically and hence these values are illustrative only. These numbers are referenced in brackets and italics throughout the narrative.
Table 10.1
Clinical innovation per course measured in QALYs for three drugs compared to their up to three alternatives: a hypothetical example
Comparison | Rathmab (R) | Araamax (A) | Araamaxplus (A+) |
|---|---|---|---|
Compared to placebo (QALYs) | 0.05(d) | 0.1(d) | 0.22 |
Compared to Rathmab (QALYs) | n/a | 0.05(e) | 0.17 |
Compared to Araamax (QALYs) | n/a | n/a | 0.12 |
Table 10.2
Price, manufacturing cost and economic rent per course for three: a hypothetical example
Rathmab (R) | Araamax (A) | Araamaxplus (A+) | |
|---|---|---|---|
Price per course ($) | 250 | 4,000 | 13,000 |
Cost of manufacture per course ($) | 250(c) | 500(c) | 620(h) |
Economic rent per course ($) | 0 | 3,500 | 12,380 |
Table 10.3
Incremental price per incremental health effect (IPER) for three drugs against different comparators: a hypothetical example
Comparison | Rathmab (R) | Araamax (A) | Araamaxplus (A+) |
|---|---|---|---|
Compared to placebo ($) | 5,000 | 40,000 | 59,091 |
Compared to Rathmab ($) | n/a | 75,000(a) | 75,000 |
Compared to Araamax ($) | n/a | n/a | 75,000 |
Table 10.4
Incremental manufacturing cost per additional QALY for three drugs against different comparators: a hypothetical example
Comparison | Rathmab (R) | Araamax (A) | Araamaxplus (A+) |
|---|---|---|---|
Compared to placebo ($) | 5,000(b) | 5,000(f) | 2,818(k) |
Compared to Rathmab ($) | n/a | 5,000(j) | 2,176(n) |
Compared to Araamax ($) | n/a | n/a | 1,000(i) |
Table 10.5
Incremental economic rent per additional QALY for three drugs against different comparators: a hypothetical example
Comparison | Rathmab (R) ($) | Araamax (A) ($) | Araamaxplus (A+) ($) |
|---|---|---|---|
Compared to placebo | – | 35,000(l) | 56,273(m) |
Compared to Rathmab | n/a | 70,000(g) | 72,824 |
Compared to Araamax | n/a | n/a | 74,000 |
10.4.1.1 Period 1
The Game starts in Period 1 when the Firm makes a decision about whether to invest a fixed research budget financed by internal funds into pharmaceutical R&D or do nothing. The Firm’s objective is to maximise economic rent. If the Firm invests in R&D, at the end of Period 1 they will have a new drug (Araamax) for rheumatoid arthritis. This new drug will have an additional clinical benefit compared with the best existing pharmaco-therapy (Rathmab). This additional effect is for a sub-group of patients and is a reduction in pain and stiffness to a threshold that allows normal daily living. The additional effect is experienced by: (1) all patients in the sub-group who receive the drug (intervention); (2) no patients in the sub-group who do not receive the drug (the control group); and (3) no patients who receive this drug but are outside this sub-group (control and intervention).
10.4.1.2 Period 2
If the Firm does invest in R&D in Period 1, then at the start of the Period 2, the Firm offers the Institution the new drug, Araamax, which has an IPER calculated relative to the best existing drug, Rathmab ($75,000 (a) Table 10.3). Rathmab is currently priced at its IMER (which his equivalent to pricing at marginal cost); calculated relative to placebo. ($5,000 (b) Table 10.4) The cost of producing a vial of Araamax is more than the cost of producing a vial of Rathmab. ($500 > $250 (c) Table 10.2) Each vial of Araamax “contains” more health effects compared with placebo than a vial of Rathmab compared with placebo. (0.1 > 0.05 (d) Table 10.1) This is the clinical innovation of Araamax. (0.1 − 0.05 = 0.05 (e) Table 10.1) Therefore the IMER of Araamax (compared with Rathmab)3 is greater than zero (250/0.05 = $5,000 > 0 (f) Table 10.4) and is assumed to be the same as the IMER for Rathmab (compared with placebo) ($5,000 (b) Table 10.4). This means there is clinical innovation (more health effects per vial) but no manufacturing innovation (the incremental costs of manufacturing each incremental health gain is the same for Araamax versus Rathmab and Rathmab versus placebo).
The Firm makes no economic rent on the non-clinically innovative units of Araamax because these are priced at their IMER. However, on every unit of additional health effect (Araamax compared with Rathmab) sold, the difference in the IPER and the IMER of these additional health effects represents economic rent to the Firm on the innovative health effects, the IπER ($75,000 − $5,000 = $70,000 (g) Table 10.5).
The Institution can choose to reimburse Araamax or do nothing. The Institution seeks to maximise the health of the population given the existing budget. If the Institution is indifferent to the payoff of reimbursement compared with that for doing nothing, it must choose to reimburse. If the Institution chooses to reimburse Araamax, it will reimburse it for all patients who are in the sub-group for which there is an effect. None of the patients who currently have their access to Rathmab subsidised will continue to be prescribed Rathmab. Instead they will all be prescribed Araamax, which is clinically superior. If Araamax is not reimbursed, no patients will have the new drug due to its very high annual cost (around 75 % of the average salary of a person with severe RA).4 In this way the health effect of the policy to reimburse Araamax is discrete rather than continuous.
The Institution, which has a fixed budget, must displace existing services to finance the additional cost of the new drug for every year that Araamax continues to be the best available pharmaco-therapy for these patients. Furthermore, once Araamax is reimbursed, it cannot be displaced until a new drug that is clinically superior for this group of patients is reimbursed; Araamax cannot be displaced to finance a different programme or a new drug for which it is not a clinical substitute. The health budget is allocatively efficient at the start of Period 2; there is no alternative allocation of resources across existing inputs and technologies that can improve health outcomes for the population. There is also no investment in improved practice that can be made today that will have returns of a lower aICER for a programme in the future that offsets the health effects foregone today due to the initial investment. Finally, if Araamax is reimbursed, it is financed by optimal displacement (d = m). The contracted programme is unpatented and continuous, that is, it can be contracted or expanded by any unit and there will be a corresponding decrease or increase in health effects.
If Araamax is reimbursed at the start of Period 2 then the Firm will produce it at an IMERc 1 ($5,000 (f) Table 10.4). At the start of Period 2 the Firm has to decide whether it will use some of the economic rent from the production and sale of Araamax to develop a new RA drug, or whether it will no longer innovate and simply continue to produce Araamax. The Firm’s payoff to continuing to manufacture Araamax will be the economic rent from the sale of the drug in Periods 2 and 3. If the Firm decides to invest in the development of a new RA drug, it will incur a cost of R&D in Period 2 in addition to the cost of manufacturing Araamax. It will also be in receipt of the revenue from the sales of Araamax in Period 2.
10.4.1.3 Period 3
If the Firm chose not to invest in R&D in Period 2 then in Period 3 the Firm continues to manufacture Araamax and the Institution continues to displace services to finance its additional cost and reimburse Araamax for eligible patients.
If the Firm chose to invest in R&D in Period 2 then at the end of Period 2 the Firm has a new drug, Araamaxplus, a more effective drug than Araamax. The gain compared with Araamax is both clinically and statistically significant. It works for the same patient group as for Araamax and if Araamaxplus is approved for reimbursement then all patients who currently receive Araamax will instead be prescribed Araamaxplus. If the Institution chooses to reimburse Araamaxplus it must displace additional services to finance the additional cost of these additional health effects.
10.4.1.4 Political Economy
This narrative contains two aspects of the political economy of the reimbursement process.
1.
If the Institution is indifferent between reimbursing the new drug and continuing funding the existing drug, it must select the new drug.
2.
The Institution cannot displace a drug that it has reimbursed to finance care for the same or different group of patients; it can only replace it with a superior drug for the same patient group.
10.4.1.5 The Relationship Between IMERs, IPERs, Expenditure and Costs of Manufacturing
This Game introduces the possibility that a future drug can have both clinical and manufacturing innovation; a reduction in the average cost of manufacturing each incremental QALY compared to either placebo or the previous drug. It also demonstrates how successive drugs capture the economic rent of previous drugs as a consequence of the combined effect of new drugs being introduced before comparators are off-patent and the application of CEA i .
Tables 10.1 to 10.5 set out a hypothetical example of the drugs that this Game characterises. These tables illustrate some of the characteristics of IMER, IPERs and IπERs in the case of drugs reimbursed successively. Araamaxplus has clinical innovation. If Araamax is still on patent and the IPER > IMER5 then the economic rent appropriated by the Firm in relation to the clinically innovative health effects of Araamax relative to Rathmab ($70,000 (g) Table 10.5), are also available on the sale of Araamaxplus. This is in addition to the IπER available on the clinically innovative health effects of Araamaxplus compared with Araamax. (See Pekarsky [2012, Appendix 6) for a discussion of the appropriation of first drug in class surplus by subsequent drugs.]
Now consider the consequences for the IπER of Araamaxplus (compared to Araamax) if there is manufacturing innovation. The additional cost of manufacturing a course of Araamax relative to Rathmab ($500 (c) − $250 (c) = $250 Table 10.2) is more than the additional cost of manufacturing a course of Araamaxplus relative to Araamax ($620 (h) − $500 (c) = $120 Table 10.2). Also, Araamaxplus has an IMER on the innovative units relative to Araamax ($1,000 (i) Table 10.4) that is less than the IMER of the clinically innovative units of Araamax relative to Rathmab ($5,000 (f) Table 10.4). Therefore there is manufacturing innovation relative to both Rathmab ($2,818 (k) < $5,000 (b) Table 10.4) and Araamax ($2,176 (n) < $5,000 (f) Table 10.4). This innovation reduces the average cost of producing additional health effects. The IPER is the same for the innovative units of Araamax and Araamaxplus, Araamaxplus appropriates Araamax’s economic rent and the average cost of manufacture of all of these health effects is reduced. Hence, the economic rent on all clinically innovative health effects relative to placebo is increased for Araamaxplus compared with Araamax ($35,000 (l) < $56,273 (m) Table 10.5). This means that with the same conventionally calculated IPER for Araamaxplus and Araamax, the economic rent for the new drug is higher due to the effect of the manufacturing innovation.
10.4.2 Game Structure
There are two players (the Firm and the Institution). It is a dynamic (consecutive decisions) three-period game of complete (public) and perfect (no uncertainty) information, therefore both players know the value of all parameters and variables with certainty at the start of the game. (We will relax these assumptions in the discussion). The game is represented as an extensive form game in Fig. 10.1.
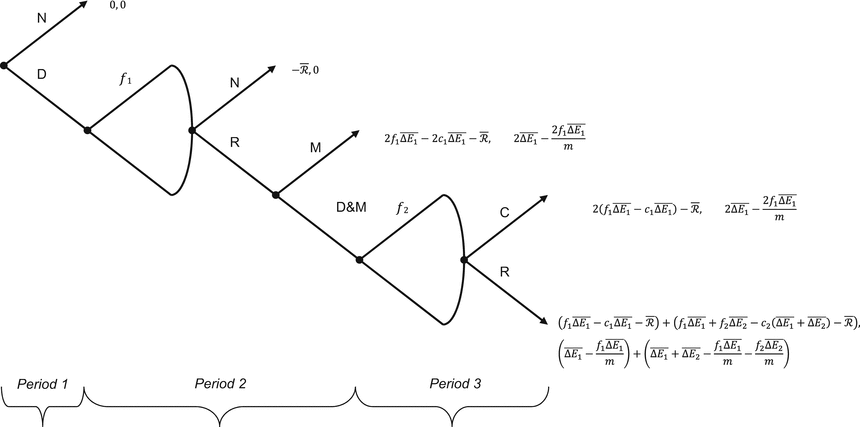
Fig. 10.1
The pharmacotherapy needs a premium game
10.4.2.1 Strategies and Payoffs
The Game starts with the Firm.
Firm
The Firm has five possible actions: Develop a new drug (D); Develop a new drug and manufacture the current drug (D&M); price the new or future drug f; manufacture the new drug only (M); or do nothing (N).
At the start of Period 1, the Firm can choose to Develop (D) or do Nothing (N). If it chooses to Develop, at the end of Period 1 it can then choose a price f 1 for the first new drug, Araamax. If the Institution chooses to reimburse the new drug at the offer price, at the start of Period 2 the Firm can then choose to either develop a second drug, Araamaxplus, while continuing to manufacture and sell Araamax (D&M) or manufacture Araamax only (M). If it develops Araamaxplus (the future drug), it must choose a price f 2 for Araamaxplus when it goes to the market at the end of Period 2.
The pay-off to the Firm from N is zero. If the Firm chooses to develop Araamax but it is not reimbursed by the Institution, its payoff is a loss of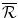 
, the fixed cost of developing a new drug. The Firm’s payoff if it manufactures and sells Araamax for two periods and does not develop a second drug is the sum of the economic rent over Periods 2 and 3:
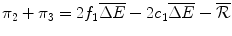
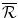, the fixed cost of developing a new drug. The Firm’s payoff if it manufactures and sells Araamax for two periods and does not develop a second drug is the sum of the economic rent over Periods 2 and 3: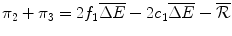(10.1)
where the revenue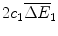 
comprises the sales of health gains 
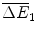at price f 1 over these two periods less the fixed cost of R&D 
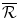and the variable cost of manufacturing 
.
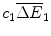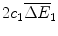comprises the sales of health gains 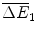at price f 1 over these two periods less the fixed cost of R&D 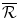and the variable cost of manufacturing 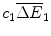.Finally, the economic rent in Periods 1 to 3 if Araamaxplus is developed in Period 2 and is reimbursed by the Institution is:
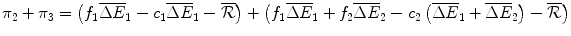
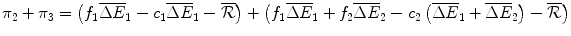
(10.2)
where:
Araamaxplus has gains of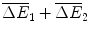
compared with the original drug Rathmab, and 
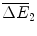compared with Araamax.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
