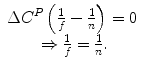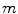The Health Shadow Price and the Economic Context

(1)

University of South Australia, Adelaide, Australia

Abstract

The value of clinical innovation of a new drug is specific to a particular clinical context; the patient group, the clinical protocol and the best alternative therapy. Similarly, the economic value of a given clinical value of innovation is specific to a particular economic context; the financial costs of the proposed and existing therapy, the method of financing the additional costs (budget expansion or displacement of services), the efficiency of the existing allocation and the competition in the market for health inputs. In Chap. 8 the ways in which the health shadow price, β _cand Economic value of clinical innovation, EVCI, capture the economic context of the health budget are illustrated. β _cis derived for four different economic contexts. I show that when the budget is fixed and allocatively inefficient: β _c = (1/n − 1/m + 1/d) ^ (−1) where n is the average Incremental Cost-Effectiveness, aICER, of the most cost-effective existing technology or programme (in expansion), m is the aICER of the least cost-effective of currently funded technologies or programmes (in contraction) and d is the aICER of the services displaced to finance the additional costs, ΔC ^P, of the new drug. The health shadow price is conditional on an economic context, indicated by c. The economic context is defined by factors including the sub-optimality of displacement (m–d), the level of allocative inefficiency in the health budget (m–n), the additional costs that need to be financed (ΔC ^P) and the current price structure in the health input market.

7.1 The Reimburser’s Problem

The Reimburser understands that β _cis derived within:

A strategy of reimbursement (adoption and financing);
An economic context that includes alternative ways to produce health effects; and
A health budget that may or may not be economically efficient.

The Reimburser also understands that the best alternative strategy to the strategy of reimbursement of the new technology need not be an actual physical option available to her. Following the definition of opportunity cost from Buchanan (2008) she understands that the best alternative strategy simply needs to represent the alternative resource allocation that maximises the payoff. Hence the choice of the alternative strategy to reimbursement can compensate, at some level at least, the failure of the institution to consider reimbursement of unpatented and unpatentable strategies.

The Reimburser also understands that a threshold IPER for a new drug derived from the health shadow price will accommodate the economic context, for example, the competition in the market to produce health effects. In contrast, a threshold IPER for the drug derived from a maxWTP for health effects will not accommodate the full economic context. However, the Reimburser does not yet understand how the health shadow price accommodates the characteristics of the health budget.

The Reimburser asks two questions.

How does β _cvary across different reimbursement strategies and economic contexts?
Why can PEA and not HTA/CEA accommodate the economic context?

The Health Economic Adviser develops four scenarios that illustrate β _cand the EVCI under reimbursement, where adoption is financed in two different ways. The first scenario is an algebraic presentation of the case presented in the previous chapter. The remaining three scenarios illustrate reimbursement under a fixed budget and a range of economic conditions, including allocative inefficiency. These scenarios also illustrate situations of optimal and suboptimal displacement. The nominated strategy in all cases is to reimburse a new drug. The financing of that drug and economic conditions vary across each scenario as summarised in Table 7.1.

Table 7.1

Four scenarios of economic context

Characteristic	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Adopting a new drug	Yes	Yes	Yes	Yes
Budget	Expandable	Fixed	Fixed	Fixed
How is additional cost of the drug financed?	Expanding budget	Displacing programmes	Displacing programmes	Displacing programmes
Price distortions?	Only new drug	Only new drug	Only new drug	Only new drug
Is current budget efficient?	Economically efficient	Economically efficient	Allocatively inefficient	Technically inefficient
Is displacement optimal? (least cost-effective program displaced)	Not applicable	Optimal or suboptimal	Optimal or suboptimal	Optimal or suboptimal

Note

All analysis and discussion in this book is concerned solely with new drugs that have clinical innovation ΔE > 0 and an additional cost ΔC > 0. The limitations of the ICER under cases where one or both of these conditions is not met are recognised but are not relevant to this discussion. Hence the ICER_iand the conventional net benefit, NB_iare interchangeable as summary metrics of the decision to adopt a new drug.¹

7.2 Scenario 1: Adoption Financed by Expansion of an Economically Efficient Budget

A Reimburser in a fictional country is required ² to increase the health budget by an amount ΔC ^P > 0 and adopt a new drug, P. This requirement to purchase the new drug is a consequence of the new drug being clinically innovative, and in this fictional country, any drug that is clinically innovative must be reimbursed, regardless of the price of that drug. New drug adoption financed by budget expansion is the nominated strategy. The budget is currently economically efficient.

The new technology, Drug P, has an offer price expressed as an IPER f > 0 and an additional effect compared with the best alternative therapy (clinical value of innovation) for this group of patients of:

$$$ \mathrm{C}\mathrm{V}\mathrm{I}=\frac{\Delta {C}^P}{f}>0, $$” src=”/wp-content/uploads/2017/03/A317514_1_En_7_Chapter_Equa.gif”></DIV></DIV></DIV></DIV><br /> <DIV class=Para>where Δ<SPAN class=EmphasisTypeItalic>C</SPAN> <SUP><SPAN class=EmphasisTypeItalic>P</SPAN> </SUP> > 0 is the additional financial cost of the new drug.</DIV><br /> <DIV class=Para>The Reimburser also identifies the most cost-effective (in expansion or adoption)<A id=Fn3_source href=$ ³ of the existing programmes; Programme N at an aICER of n > 0. This is an opportunity to increase the health of the population by an amount:

$$$ \frac{\Delta {C}^P}{n}=\Delta {E}^N>0, $$” src=”/wp-content/uploads/2017/03/A317514_1_En_7_Chapter_Equb.gif”></DIV></DIV></DIV></DIV><br /> <DIV class=Para>Expansion of Programme N is the best alternative strategy.<A id=Fn4_source href=$ ⁴ It is the action with the maximum possible gain that also meets the condition of being financed by expanding the budget constraint by an amount ΔC ^P. (See Sect. 6.3.1.) This scenario is illustrated in Fig. 7.1.

Fig. 7.1

Scenario 1: expandable budget

The shadow price (λ) of the budget constraint (B), defined in terms of expansion (e) and measured as an ICER is:

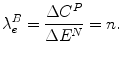
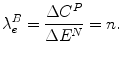
${\lambda}_e^B=\frac{\Delta {C}^P}{\Delta {E}^N}=n.$

This result is the aICER of the additional effects ΔE ^Nof the most cost-effective programme in expansion, where the additional cost of this programme is financed by expanding the health budget by an amount ΔE ^P.

The net financial cost of Strategy R is:

$$$ \Delta {C}^P>0. $$” src=”/wp-content/uploads/2017/03/A317514_1_En_7_Chapter_Equd.gif”></DIV></DIV></DIV></DIV><br /> <DIV class=Para>This is the additional financial cost to the health budget of reimbursing the new drug and it is financed by expansion of the budget.</DIV><br /> <DIV class=Para>The net health benefit of Strategy R is:<br /> <DIV id=Eque class=Equation><br /> <DIV class=EquationContent><br /> <DIV class=MediaObject><IMG alt=$ 0. $$” src=”/wp-content/uploads/2017/03/A317514_1_En_7_Chapter_Eque.gif”>

This is the net health gain to the population as a consequence of reimbursement. This is the same as the gain to the target patients because in this scenario, no services need to be displaced to finance the additional cost of the new drug.

The NEBh of Strategy R (NEBh^R) is:

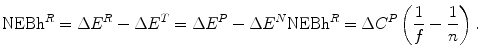
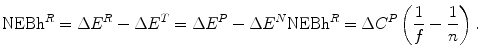
${\mathrm{NEBh}}^R=\Delta {E}^R-\Delta {E}^T=\Delta {E}^P-\Delta {E}^N{\mathrm{NEBh}}^R=\Delta {C}^P\left(\frac{1}{f}-\frac{1}{n}\right).$

(7.1)

This is the gain in health effects for the population as a consequence of Strategy R, ΔE ^R, constrained by the health effects, ΔE ^T, of the best alternative use of the expanded budget, Strategy 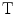$\mathrm{T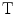}$ . (See Fig. 7.1).

The health shadow price of the health effects of the new drug is an IPER for the new drug such that the Reimburser is indifferent to the Strategy R and the best alternative strategy, T, that is, the net economic benefit of reimbursement is zero:

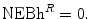
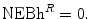
${\mathrm{NEBh}}^R=0.$

Substituting this result in Eq. (7.1) we have:

$\begin{array}{c}\hfill \Delta {C}^P\left(\frac{1}{f}-\frac{1}{n}\right)=0\hfill \\ {}\hfill \Rightarrow \frac{1}{f}=\frac{1}{n}.\hfill \end{array}$

If f = n then the net economic benefit (health) of reimbursement is 0, therefore the health shadow price is:

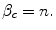
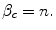
${\beta}_c=n.$

The key parameters derived in this scenario are summarised in Table 7.2 and discussed in Sect. 7.6.

Table 7.2

Comparison of the value of the key parameters under the four scenarios of economic context

Parameter	Scenario 1: economic efficiency and financed by budget expansion	Scenario 2: economic efficiency and financed by displacement	Scenario 3: allocative inefficiency and financed by displacement	Scenario 4: technical inefficiency and financed by displacement
Clinical value of innovation (target patients) ΔE ^P	CVI = ΔE ^P	CVI = ΔE ^P	CVI = ΔE ^P	CVI = ΔE ^P
Net health effects from reimbursement (population) ΔE ^R	ΔE ^R = ΔE ^P − 0 = ΔE ^P	ΔE ^R = ΔE ^P − ΔE ^D	ΔE ^R = ΔE ^P − ΔE ^D	ΔE ^R = ΔE ^P − ΔE ^D
Conventional Net Benefit NB (k)	NB_k = kΔE ^P − ΔC ^P	NB_k = kΔE ^P − ΔC ^P	NB_k = kΔE ^P − ΔC ^P	NB_k = kΔE ^P − ΔC ^P
Net economic benefit from reimbursement (health) NEBh^R	NEBh^R = ΔE ^R − ΔE ^N	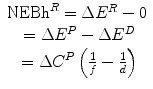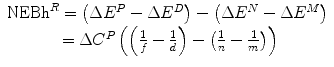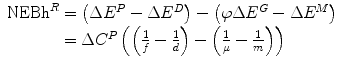$\begin{array}{c}\hfill {\mathrm{NEBh}}^R=\Delta {E}^R-0\hfill \\ {}\hfill =\Delta {E}^P-\Delta {E}^D\hfill \\ {}\hfill =\Delta {C}^P\left(\frac{1}{f}-\frac{1}{d}\right)\hfill \end{array}$	$\begin{array}{c}\hfill {\mathrm{NEBh}}^R=\left(\Delta {E}^P-\Delta {E}^D\right)-\left(\Delta {E}^N-\Delta {E}^M\right)\hfill \\ {}\hfill =\Delta {C}^P\left(\left(\frac{1}{f}-\frac{1}{d}\right)-\left(\frac{1}{n}-\frac{1}{m}\right)\right)\hfill \end{array}$	$\begin{array}{c}\hfill {\mathrm{NEBh}}^R=\left(\Delta {E}^P-\Delta {E}^D\right)-\left(\varphi \Delta {E}^G-\Delta {E}^M\right)\hfill \\ {}\hfill =\Delta {C}^P\left(\left(\frac{1}{f}-\frac{1}{d}\right)-\left(\frac{1}{\mu }-\frac{1}{m}\right)\right)\hfill \end{array}$
Net financial cost of adoption (target patients) ΔC ^P	ΔC ^P	ΔC ^P	ΔC ^P	ΔC ^P
Net financial effect of reimbursement (Population) ΔC ^R	ΔC ^R = ΔC ^P	ΔC ^P − ΔC ^P = 0	ΔC ^P − ΔC ^P = 0	ΔC ^P − ΔC ^P = 0
Health shadow price β _c	β _c = n	β _c = d	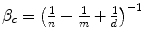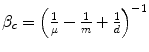${\beta}_c={\left(\frac{1}{n}-\frac{1}{m}+\frac{1}{d}\right)}^{-1}$	${\beta}_c={\left(\frac{1}{\mu }-\frac{1}{m}+\frac{1}{d}\right)}^{-1}$
Shadow price of the budget in expansion λ _e^B	λ _e^B = n	Unknown/not defined	Unknown/not defined	Unknown/not defined
Shadow price of the budget in expansion conditional on initial contraction λ _e\|c^B	n/a	λ _e\|c^B = n = m	Unknown	Unknown
Economic value of clinical innovation EVCI	EVCI = nΔE ^P	EVCI = dΔE ^P	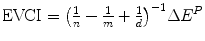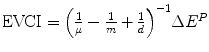$\mathrm{EVCI}={\left(\frac{1}{n}-\frac{1}{m}+\frac{1}{d}\right)}^{-1}\Delta {E}^P$	$\mathrm{EVCI}={\left(\frac{1}{\mu }-\frac{1}{m}+\frac{1}{d}\right)}^{-1}\Delta {E}^P$