(1)
Department Cell and Molecular Biology, John A. Burns School of Medicine, University of Hawaii, Honolulu, HI, USA
Abstract
Fluorescence methods are often employed for the characterization of molecular interactions. In particular, polarization/anisotropy studies are widely utilized in the life sciences as they allow quantification of protein interactions in the micro- and nanomolar concentration range. Herein we shall briefly describe the theoretical aspects of polarization/anisotropy and outline an experiment for determination of the dissociation constant for a protein–ligand complex.
Key words
PolarizationAnisotropyProtein interactionProtein–ligand binding1 Introduction
Fluorescence methodologies have been used in the biological and biochemical fields since the first half of the last century [1, 2]. Fluorescence studies offer unique advantages over traditional biochemical approaches to ligand–protein interactions, such as column chromatography or radiolabeling, by providing information down to subnanomolar concentrations. The characterization and understanding of the forces driving these interactions are of critical importance since biological specificity, essential to life, is largely based on protein–ligand interactions. In many cases, the intrinsic protein fluorescence, largely due to tryptophan and to a lesser extent tyrosine residues [3], can be used to monitor the protein interaction. In other cases, an extrinsic fluorescence probe can be attached to the protein or ligand. Although direct intensity measurements can be valuable for detecting protein interactions, in some cases, the fluorescence intensity change upon ligand binding is negligible [4, 5]. In these cases, protein interactions can often be monitored using polarization, which relies on the differences in rotational mobility of bound vs. free ligand; hence a change in fluorescence yield or spectral shift is not required. Polarization studies have been used by biochemists for studying protein interactions for more than 50 years as the theory had been thoroughly developed and tested by Francis Perrin and Gregorio Weber [6, 7]. However, the introduction of the TDx polarization instrument for fluorescence immunoassays by Abbott Laboratories in the early 1980s [8] as well as the development of polarization plate readers soon thereafter significantly increased the use of this method because it introduced a broader community to the rapid screening of a large number of protein–ligand combinations. Polarization has since become one of the most prominent methods for investigating protein interaction as polarization measurements are done at equilibrium (no need to separate bound and free) and can be easily automated [9].
Herein we demonstrate how to use fluorescence polarization to determine the fraction of bound and free ligand when monitoring protein–ligand interaction. We start with a large excess (relative to the K d) of the species (protein or ligand) that is not being monitored, such that all of the fluorescent ligand or protein is bound. Successive dilution of the sample not being monitored (e.g., ligand), while maintaining the concentration of the monitored substance (e.g., protein), provides a complete binding isotherm. In case the emission intensity changes during the outlined experiment, this change is taken into account, as outlined in the theory section, when determining the fraction bound. We note that in the case of significant intensity changes, there is no need to measure fluorescence polarization/anisotropy to follow the binding. But we also note that intensity is an “extensive property,” i.e., it depends on the amount of material present, while polarization/anisotropy is an “intensive property,” which is independent of the amount of material (the fluorescence lifetime is also an intensive parameter). There are often advantages to the use of intensive parameters, for example, the fact that they are independent of the instrument platform being used for the measurements. From the plot of fraction bound and protein concentration, we quantify the dissociation constant (K d) for this protein–ligand pair. An example, from the literature, is also provided in which the polarization change of the ligand is monitored, as well as an example determining the strength of protein–protein interaction [10, 11]. A similar procedure, along with a rigorous treatment of attendant errors, has been described previously [12] and has been used to determine dissociation constants in a number of reports [13, 14].
1.1 Theory
For a molecule to fluoresce, an energy source capable of promoting the molecule to an excited state must be utilized. The most common way of achieving these specific energies is through a xenon arc lamp and a monochromator, which allows for the selection of wavelengths in the range of 200–1,000 nm. To achieve polarized emission from the sample, a specific electric vector of the excitation light must be isolated as the excitation source typically has electronic radiation aligned in all directions within the plane perpendicular to the propagation of the light. This isolation is traditionally done by placing a polarizer orientated parallel to the laboratory axis just after the light source. Such polarization of light allows for the specific excitation of fluorophores that have excitation vectors aligned properly with the plane-polarized excitation light. This phenomenon is termed photoselection. The polarization (P) is then determined by measuring emission through a polarizer parallel (I ||) and perpendicular (I ⊥) to the excitation light:
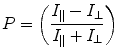
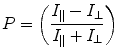
(1)
Another frequently used expression, in the context of polarization, is anisotropy and is defined as:
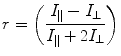
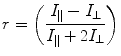
(2)
The information content from polarization and anisotropy is essentially identical [15] and can be interconverted using the expression:
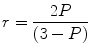
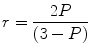
(3)
Some researchers fervently adhere to the use of the polarization function, while others cling just as fervently to the anisotropy function. We simply note that anisotropy is probably the more popular function in biophysical studies, while polarization is almost universally used in clinical chemistry application. The limits of polarization, in a completely orientated system like a crystal, are +1 or −1 (+1 or −0.5 for anisotropy) as defined by the equations above. However, in the case of a solution of fluorophores, these theoretical limits are not reached. This partial depolarization is due to the random orientation of the electric vector of each molecule in an ensemble of randomly oriented fluorophores. The limits for these cases have been derived, based on photoselection rules, as +0.5 and −0.33 for polarization or +0.4 and −0.2 for anisotropy [7]. A number of factors contribute to the observed polarization of a fluorophore. One of the factors, which is a measure of polarization of the fluorophore in the absence of rotation, is termed the limiting polarization (P 0) and is determined:
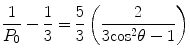
where θ is the angle between absorption and emission oscillator.
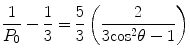
(4)
Polarization measures the rotational mobility of the fluorescent molecule, which makes it more appealing for monitoring interactions than intensity measurements. In 1925–1926, Francis Perrin derived an expression for obtaining the polarization based on the rotational diffusion and excited state lifetime [6]:
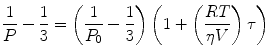
where P is the polarization observed, P 0 is the limiting polarization of the fluorophore, R is the gas constant, T is the absolute temperature, V is the molar volume of the fluorescent molecule, η is the solvent viscosity, and τ is the excited state lifetime. This equation is often rewritten to contain the Debye rotational relaxation time (ρ):
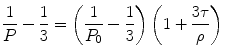
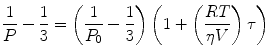
(5)
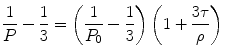
(6)
The major advantage of polarization, compared to the other methods, is its ability to quantify the extent of bound ligand in a sample without recourse to a separation step, as, for example, is required with radioisotope labeling. This mathematical resolution of free from bound is accomplished through the additivity of polarization of different species, which was derived by Gregorio Weber in 1952 [7]:
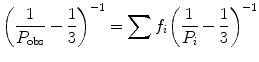
where P obs is the actual observed polarization coming from all the components, f i is the fractional contribution of the ith component to the photocurrent, and P i is the polarization of the ith component. Additivity for anisotropy can also be expressed as:
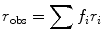
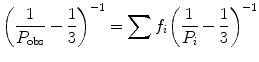
(7)
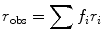
(8)
As can be deduced from the previous equations, a change in fractional contribution to the photocurrent of the bound or free fluorophore during the experiment will alter their contributions in the additivity equation. This bias can be corrected, when solving for the fraction bound (f b), by taking into account the change in intensity of the bound fluorescent ligand, termed g, namely,
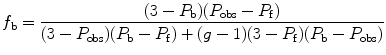
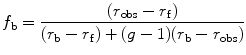
where P obs is the observed polarization, P f is the polarization of the free ligand, and P b is the polarization of the bound ligand. An expression for anisotropy, which takes into account changes in intensity (g), is also shown above where r obs is the observed anisotropy, r f is the anisotropy of the free ligand, and r b of the bound one.
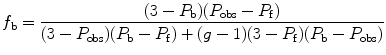
(9)
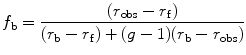
(10)
The dissociation constant corresponding to a reversible equilibrium between a protein (P), a ligand (L), and a protein–ligand complex (PL) is given by:
![$$ {K_{\mathrm{ d}}}=\frac{{[\mathrm{ P}][\mathrm{ L}]}}{{[\mathrm{ P}\mathrm{ L}]}} $$](/wp-content/uploads/2017/03/A299540_1_En_2_Chapter_Equ000211.gif)
(11)
Determination of this dissociation constant requires determination of the concentration of bound ligand (PL) as a function of the total protein (PT) and ligand (LT) concentrations:
![$$ [\mathrm{ PL}]=\frac{{({K_{\mathrm{ d}}}+{{\mathrm{ L}}_{\mathrm{ T}}}+{{\mathrm{ P}}_{\mathrm{ T}}})-\sqrt{{\left[ {{{{({K_{\mathrm{ d}}}+{{\mathrm{ L}}_{\mathrm{ T}}}+{{\mathrm{ P}}_{\mathrm{ T}}})}}^2}-4{{\mathrm{ P}}_{\mathrm{ T}}}{{\mathrm{ L}}_{\mathrm{ T}}}} \right]}}}}{2} $$](/wp-content/uploads/2017/03/A299540_1_En_2_Chapter_Equ000212.gif)
(12)
Dissociation constants for the protein–ligand system can then be determined by fitting a plot of f b vs. concentration to the following equation:
![$$ {f_{\mathrm{ b}}}=\frac{{[\mathrm{ Protein}]}}{{[\mathrm{ Protein}]+{K_{\mathrm{ d}}}}} $$](/wp-content/uploads/2017/03/A299540_1_En_2_Chapter_Equ000213.gif)
(13)
2 Materials
All solutions were made up using ultrapure water (specific resistance 17.5 MΩ) collected from a Barnstead Nanopure II at 25 °C and, when required, filtered through a 0.22 μm filter from Millipore. Buffer and protein stocks were stored at 4 °C. Stock solutions of furosemide were stored at room temperature:
1.
Monomeric HSA (mHSA): ~1 mM stock solution isolated from lyophilized, 99 % agarose gel electrophoresis, HSA from Sigma (St. Louis, MO, USA). See Subheading 3.1 for purification procedure. (We note that lyophilized HSA typically contains about 10–15 % of a covalent dimer and higher oligomers due to exchange of disulfide cross-links within the protein population [16].)
2.
Furosemide: 850 μM (0.28 g/L) stock solution was made in 0.05 M HEPES, pH 7.0 (Sigma, St. Louis, MO, USA).
3.
Sephacryl S300 buffer: 0.05 M HEPES, pH 7.5, and 0.05 M NaCl. Weigh out 11.9 g of HEPES powder and 2.9 g NaCl. Dissolve in ~900 mL. Adjust the pH to 7.5 with 2 M NaOH. Add ~100 mL of water to make 1 L. Filter through a 0.22 μm and store at 4 °C.
4.
Sephacryl S300 column: Contained in a Pharmacia XK16 column with ~120 mL of S300 resin. Column stored in S300 buffer or, for long-term storage, in 70 % ethanol.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
