Fig. 4.1
A graphical representation of the compound optimization process
The next chapter is a thorough summary of practical and statistical aspects of analyzing data from large-scale screening campaigns.
Phenotypic screens may lend themselves to a more streamlined process. The measurement of the phenotype is likely made using cell-based assays or possibly an in vivo assay. In these cases, higher quality hits may be found. For example, if a compound has poor properties (e.g., permeability) it will not be able to enter the cell and therefore show little efficacy. Similarly, potential toxicities are more likely to be demonstrated in these screens than in simple ligand-binding biochemical assays. For example, cell-based assays can usually be supplemented with cell viability assays to obtain rudimentary estimates of toxicity.
4.5 Assay Data in Drug Discovery
As one might expect, there are usually a large number of assays used to optimize molecules and these vary in complexity and type. The primary pharmacology assays are usually related to potency against the target or phenotype. In traditional target-based projects, initial potency measurements are from simple biochemical ligand-binding assays. Compounds that show sufficient activity against the target are then run against some type of functional assay to verify the relevance of the hit.
The initial screen for potency is often conducted at a single concentration; molecules that prove interesting might then be followed by a dilution series of the concentration to verify that a dose-response relationship exists. To do this, the assay value is determined over a range of concentrations and a statistical dose-response model is fit to the data. Figure 4.2 shows an example of such a dataset from a phenotypic screen where the assay outcome is larger for more potent compounds. One common method for quantifying the potency of a compound is to calculate the effective concentration or EC. For these data, we fit a four parameter logistic model to the assay data using standard nonlinear regression methods that assume normally distributed errors:
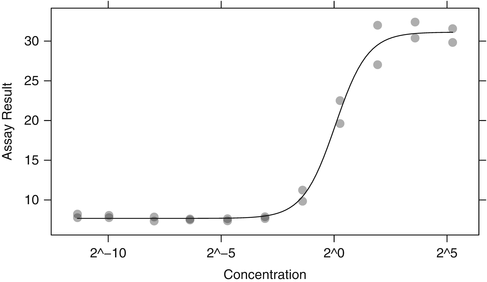
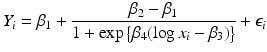 where β 1 is the minimum value of the outcome, β 2 is the maximum, β 3 is the concentration that corresponds to a 50 % increase in the outcome, β 4 is a parameter for the slope of the curve and
where β 1 is the minimum value of the outcome, β 2 is the maximum, β 3 is the concentration that corresponds to a 50 % increase in the outcome, β 4 is a parameter for the slope of the curve and 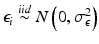 ,
, 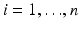 . It is common to estimate the concentration that delivers 50 % effectiveness, known as the EC 50. For these data, there is a good dose-response and an acceptable model fit that yields
. It is common to estimate the concentration that delivers 50 % effectiveness, known as the EC 50. For these data, there is a good dose-response and an acceptable model fit that yields 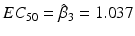 with a 95 % confidence interval of (0.898, 1.198). Had the data for this compound not shown a systematic increase in the assay result, we would be more likely to consider the hit an aberration. Single concentration assays are easily amenable to high throughput screens where thousands or a million-plus compounds may be tested. Failure to show a dose-response for a suitable concentration range can be a cause for a compound’s attrition despite initial results.
with a 95 % confidence interval of (0.898, 1.198). Had the data for this compound not shown a systematic increase in the assay result, we would be more likely to consider the hit an aberration. Single concentration assays are easily amenable to high throughput screens where thousands or a million-plus compounds may be tested. Failure to show a dose-response for a suitable concentration range can be a cause for a compound’s attrition despite initial results.

Fig. 4.2
A typical dose-response experiment with a nonlinear regression line to estimate the effective concentration
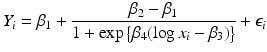
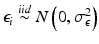 ,
, 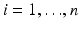 . It is common to estimate the concentration that delivers 50 % effectiveness, known as the EC 50. For these data, there is a good dose-response and an acceptable model fit that yields
. It is common to estimate the concentration that delivers 50 % effectiveness, known as the EC 50. For these data, there is a good dose-response and an acceptable model fit that yields 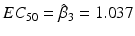 with a 95 % confidence interval of (0.898, 1.198). Had the data for this compound not shown a systematic increase in the assay result, we would be more likely to consider the hit an aberration. Single concentration assays are easily amenable to high throughput screens where thousands or a million-plus compounds may be tested. Failure to show a dose-response for a suitable concentration range can be a cause for a compound’s attrition despite initial results.
with a 95 % confidence interval of (0.898, 1.198). Had the data for this compound not shown a systematic increase in the assay result, we would be more likely to consider the hit an aberration. Single concentration assays are easily amenable to high throughput screens where thousands or a million-plus compounds may be tested. Failure to show a dose-response for a suitable concentration range can be a cause for a compound’s attrition despite initial results.Secondary pharmacology assays are usually associated with toxicity endpoints and perhaps ADME properties. The phrase “secondary pharmacology” is most associated with the former but can also include assays to determine the drug-likeness of the initial hits. For example, lipophilicity, permeability and other factors are important considerations when developing drugs. Other factors are also evaluated such as the ease of synthesis, if the molecule is amenable to parallel/combinatorial chemistry, etc. Additionally, when the target is part of a gene family selectivity assays can be instrumental in ensuring that an appropriate and specific potency is achieved. In the previously mentioned JAK-STAT pathway, four important genes are JAK1, JAK2, JAK3 and Tyk2. When optimizing the chemistry, there may be interest in determining the potency of one target to another and this may be measured using the ratios of EC 50 values for a pair of these genes.
The following sub-sections in this chapter discuss aspects of assay data and how statistics can be used to increase assay quality. Chapter 8 describes the design and analysis of an in vivo assay to characterize cardiac safety liabilities.
When considering the particulars of assay data, there is more than one perspective to contemplate. One might consider the delineation between the producers (i.e., the screening groups) and the consumers (including medicinal chemists, biologists and project teams) of the assay. Each group has their own set of conflicting objectives for assay data and it is often the case that a successful drug discovery project is one that considers both viewpoints. Statisticians may be in a position to mediate between these groups and the last subsection below discusses a method for facilitating such a discussion.
4.5.1 Important Aspects of Assay Data
During the assay development phase it is advantageous to characterize the nature of the assay outcome so that this information can be used to properly analyze the data. If the assay result is appreciably skewed, transformations of the data are likely to be needed. It is important to discuss these findings with the scientists; often naturally skewed data are mistaken for symmetric data with outliers. Outlier identification techniques tend to have poor properties when dealing with very small samples sizes and can be counter-productive in this context. Also, when working with EC 50 data, there is the potential for off-scale results when 50 % inhibition was not achieved at the largest dose. In this case, censored data arises (Kalbfleisch and Prentice 1980) and the data are usually reported as “ > C max ” where C max is the largest dose used in the experiment (left-censoring can also occur but is less common). Many scientists are unaware of the effects of censoring and the available data analysis methods that can be used. As such, it is not uncommon for a censored data point to be replaced with C max . This can lead to serious bias in mean estimates and severely underestimate the variance of the mean since multiple censored values would result in the same value repeated under the guise of being known.
Scientists often work with parameters that have biological significance but whose sampling distribution may be unknown. Permeability is commonly measured utilizing Caco-2 or MDCK cells and is typically defined via a first order differential equation. The efflux ratio (Wang et al. 2005), defined here as the apparent permeability out of the cell divided by the apparent permeability into the cell,
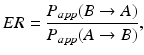 is an example of an interpretable parameter comprised of empirical estimates whose sampling distribution may not be readily apparent. Ranking compounds in terms of their efflux potential is an area where a statistician can contribute expertise. Measuring transporter activity via various assays invites parallels to inter-observer agreement problems in statistics. For example, transporter activity can be measured using various (transfected) cell lines, sandwich culture human hepatocytes (a cell-based system that can better mimic the dynamics of intact liver tissue via the formation of bile canaliculi), primary cells (intact tissue, e.g., liver slices), or via mutant in vivo animal models. Comparing in-house assay performance to that obtained using one or more contract research organizations is also possible. Apart from comparing the accuracy and precision/reproducibility of various assay estimates, cost, donor availability, amenability to automated screening systems, etc., can dictate the acceptable parameters for an assay.
is an example of an interpretable parameter comprised of empirical estimates whose sampling distribution may not be readily apparent. Ranking compounds in terms of their efflux potential is an area where a statistician can contribute expertise. Measuring transporter activity via various assays invites parallels to inter-observer agreement problems in statistics. For example, transporter activity can be measured using various (transfected) cell lines, sandwich culture human hepatocytes (a cell-based system that can better mimic the dynamics of intact liver tissue via the formation of bile canaliculi), primary cells (intact tissue, e.g., liver slices), or via mutant in vivo animal models. Comparing in-house assay performance to that obtained using one or more contract research organizations is also possible. Apart from comparing the accuracy and precision/reproducibility of various assay estimates, cost, donor availability, amenability to automated screening systems, etc., can dictate the acceptable parameters for an assay.
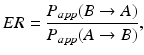
Another challenge in discovery is the general lack of absolute standards. Not surprisingly, a shortage of absolute standards facilitates the widespread use of relative measures of comparison. For example, whereas a statistician considers a standard deviation (or variance) as a meaningful summary measure for dispersion many scientists prefer to use the coefficient of variation to measure uncertainty. Relative comparisons, e.g., an assay’s relative error to a known target or another estimated quantity, are commonly used to interpret data. Fold changes are used extensively, e.g., comparing the potency of two or more compounds. Unfortunately, our experience is that the default level of evidence for equality required by many scientists is that two data points be “within twofold” of each other. This comparison may not include a careful discussion of what sources of variability were involved in forming the comparison. Also, since parameters such as bioavailability and plasma protein binding are defined as fractions, relative comparisons involving fractions occur. Propagation of error techniques such as Fieller’s theorem (Fieller 1954) and other basic results from mathematical statistics are useful. While simulation or Monte Carlo techniques can prove beneficial, the ability to determine or approximate closed form solutions should not be overlooked. Closed form solutions prove useful in approximating confidence intervals, can often be included in basic computational settings or tools, or assist with sample size calculations. Unlike later stage confirmatory clinical studies subject to regulator scrutiny, a first order approximation to an early discovery problem may provide a suitable level of rigor. Unlike some large clinical studies that recruit tens of thousands of patients, discovery efforts often involve making decisions with imperfect or limited amounts of data.
4.5.2 Improving and Characterizing Assay Quality
There are two basic phases of assay development where statistics can play an important role: the characterization and optimization of an assay. Characterization studies are important as they are an aid to understanding the assay’s operating characteristics as well as help identify areas for improvement. Improving the assay via statistical methods, such as sequential experimental design, can have a profound positive impact. The statistician would work with the scientist to understand the important experimental factors that can be explored and efficient experimental designs can be used to optimize these factors. Haaland (1989) and Hendriks et al. (1996) provide examples of this type of data analysis.
Many of the key questions for an assay are related to variation and reproducibility. For example, a characterization of the sources and magnitudes of various noise effects is very important. If some significant sources of noise cannot be reduced, how can they be managed? For plate-based assays, there may be substantial between-well variation (i.e., “plate effects”) and so on. A general term for experiments used for the purpose of understanding and quantifying assay noise is measurement system analysis. These methods are often the same as those used in industrial statistics to measure repeatability and reproducibility (Burdick et al. 2003, 2005). Two examples of such experiments are discussed in Chap. 6 Initial conversations with the assay scientists can help understand which aspects of the assay have the highest risk of contributing unwanted systematic variation and these discussions can inform subsequent experiments.
Investigations into possible sources of unwanted bias and variation can help inform both the replication strategy as well as the design of future experiments. If the sources of variation are related to within-plate effects, it may be advisable to replicate the samples in different areas of the plate and average over these data points. Also, it is common for the final assay result to be an average of several measurements (where the replicates are likely technical/subsamples and not experimental replicates). Robust summary statistics, such as the median, can mitigate the effect of outliers with these replicates. In cases where systematic problems with the assay cannot be eliminated, “Block what you can; randomize what you cannot” (Box et al. 2005). Blocking and randomization will help minimize the effect of these issues on experiments comparing different compounds. For example, some assays require donors for biological materials, such as liver cells, and the donor-to-donor variation can be significant. Unless there are enough biological materials to last through the entirety of the project, blocking on the donor can help isolate this unwanted effect. Other statistical methods, such as repeated measures analysis, can be used to appropriately handle the donor-to-donor variation but are useless if the experimental layout is not conducive to the analysis. As another example, light/dark cycles or cage layout can have significant effects on in vivo experiments and can be dealt with using blocking or randomization. These unwanted sources of noise and/or bias in experiments can be severe enough to substantially increase the likelihood that a project will fail.
Statistical process control (Montgomery 2012) can be useful for monitoring assay performance. While most compounds screened for activity are measured a limited number of times, control compounds are typically used to track assay performance across time. Multiple control compounds may be used to gauge a particular assay’s behavior over a diverse compound space. For an assay consumer, how their compound fares relative to the known behavior of one or more control compounds invites statistical comparisons. In addition to using control compound data to pass/fail individual assay results, these data are also used on occasion to adjust or scale the assay value for a compound under consideration. This can again suggest the need for applying basic concepts such as Fieller’s theorem. Comparable to the development of normalization methods used in the analysis of microarray data, methods that attempt to mitigate for extraneous sources of variability may be applied. For example, standard curves are often used where tested compounds are reported in comparison to an estimated standard profile. In part, these normalization or adjustment schemes are often used because the biologist or chemist lack engineering-like specifications for interpreting data. Use of external vendors in the early discovery process can necessitate the need for monitoring assay quality or performing inter-laboratory comparisons.
The elimination of subjectivity is also important. In in vitro experiments subjectivity can surface when assembling the data. For example, a policy or standard for handling potential outliers can be critical as well as a simple definition of an outlier. In in vivo experiments, there is a higher potential for subjectivity. Some measurements may be difficult to observe reliably, such as the number of eye-blinks. In these cases, a suitable strategy to mitigate these factors should be part of the assay protocol.
4.5.3 Conceptualizing Experimental Robustness
As previously mentioned, both the assay producer and the assay consumer can have different, perhaps opposing, views on the definition of a “fit for purpose” assay. In the end, both parties desire to have a successful experiment where a definitive resolution of an experimental question is achieved, which we term a robust experiment. Neither of these groups may have a high degree of statistical literacy and may not realize what factors (besides more common project-management related timelines and costs) influence experimental robustness. First and foremost, the consumers of the assay should have some a priori sense of what is expected from an assay. Comparable to sample size estimation procedures, some notion of the level of signal that the assay should be able to detect is critical. Two examples that we routinely encounter include:
For a single dose potency assay, the requirement might be initially stated as “reliably detect a percent inhibition greater than 50 %.”
For selectivity assays, the target might be phrased as the “ability to differentiate between a selectivity ratio of 10-fold and 50-fold.”
In the first case, more work may be needed to express the required signal in terms of a comparison, such as “be able to differentiate a 10 % difference in inhibition.” Without this information, the probability that the assay will meet the expectations of the consumers decreases. Our experience is that this requirement is rarely discussed prior to the development of the assay and is a common source of conflict that surfaces after the assay protocol has been finalized and the assay is in regular use.
The replication strategy of the assay should be informed by the required signal, the levels of noise, cost and other factors. It is important that this strategy be the result of an informed discussion between the assay producers and consumers. To this end, we frame the discussion in terms of increasing experimental robustness using a modification of a formula from Sackett (2001),
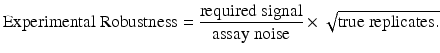 Here, the signal is related to the expectations of the experimenter. To resolve small, subtle differences between conditions would correspond to a small signal and, all other things being equal, reduce the robustness. Similarly, the magnitude of the assay noise will have a profound effect on the robustness. The third item, the number of replicates, is a proxy for the overall experimental design but this level of generality effectively focuses the discussion. This equation can help the teams understand that, in order to achieve their goal, trade-offs between these quantities may be needed.
Here, the signal is related to the expectations of the experimenter. To resolve small, subtle differences between conditions would correspond to a small signal and, all other things being equal, reduce the robustness. Similarly, the magnitude of the assay noise will have a profound effect on the robustness. The third item, the number of replicates, is a proxy for the overall experimental design but this level of generality effectively focuses the discussion. This equation can help the teams understand that, in order to achieve their goal, trade-offs between these quantities may be needed.
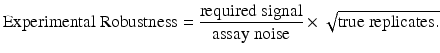
4.6 Compound Screening
During initial screening, a large number of compounds are evaluated, typically using high-throughput assays. While compound screening may be synonymous with “high throughput screening” there are several variations on how the corpus of compounds is chosen and/or assayed.
One simple approach is to screen the entire “file” of compounds (those that have been previously synthesized and have sufficient chemical matter for testing). Given the cost and logistical issues of screening such a large number of compounds, many of which may not be viable drugs, this is viewed as a sub-optimal approach.
Focused screens evaluate a subset of molecules based on some a priori criteria. For example, a project targeting the central nervous system might constrain their screen to compounds that are known or predicted to cross the blood-brain barrier. As another example, a focused screen may only include compounds that are believed to have activity against a certain target class (e.g., kinases, G protein-coupled receptors, etc.).
Fragment-based screening (Murray and Rees 2009) takes small chemical structures and screens them for activity. Here, hits are likely to have low biological activity and optimization techniques may combine two or more active fragments into a more potent molecule. Alternatively, the fragment may be used as the starting point to design new molecules.
Often, especially with target-based projects, the initial screen may be conducted with each compound tested at a single concentration. In basic biochemical screens the assay results may be the percent inhibition of the target. For phenotypic screens the experimental design and the nature of the assay endpoint can vary.
For simple initial screening designs for binding assays, there is usually an expectation that most molecules have negligible biological activity and basic statistical analysis of such data focus on finding the “outlier” signal in a sea of inactivity. This analysis has largely been commoditized in scientific software. However, there are a number of aspects of the analysis that should be reviewed based on what is known about the assay. For example, the activity values can be normalized based on the positive and negative controls but this depends on the controls being appropriate and stable over time. Also, compensating for row, column or edge effects may be required for a plate-based assay. Malo et al. (2006) is an excellent overview of statistical techniques for primary screening data.
In target-based screens, once a molecule is estimated to have sufficient potency a secondary battery of assays are used to further characterize the molecule. First, steps are taken to ensure that the hit was not an aberration by re-synthesizing the compound for repeated testing. The compounds are also evaluated for impurities (Hermann et al. 2013). A dose-response experiment is usually performed to get a more refined estimate of potency via an EC 50. If the primary pharmacological assay is biochemical, such as a ligand binding assay, a functional assay may also be run to confirm that the hit is relevant. As mentioned previously, other considerations are made regarding the molecule: the ease of synthesis, if the molecule is amenable to parallel/combinatorial chemistry, solubility, permeability, etc.
If the potency and ancillary characteristics of the compound are acceptable, the compound is usually termed a lead compound and further optimized. Depending on the project and the success rate, screening may continue to find more hits in case there are complications or unexpected issues with the current set of leads. It is common for project teams to develop one or more backup compounds in parallel with the lead compound in case an issue is found with the lead molecule.
4.7 Compound Optimization
Lead optimization is usually accomplished by taking one or more initial lead compounds and sequentially making changes to the molecules to improve its characteristics. Often, this process assumes a good structure activity relationship (SAR), meaning that changes to the molecule can yield reliable results (apart from measurement error). For example, Ganesh et al. (2014) describe the types of structural substitutions and changes that can be made to increase selectivity and other characteristics from a starting set of molecules. In our experience, many of these types of changes are based on the intuition and experience of the medicinal chemists. However, the source of structural modifications can also be suggested by quantitative, model-based methods. Chapter 6 describes techniques such as activity cliffs, Free-Wilson models and other data-driven approaches that can help predict the change in the characteristics of a molecule for a specific structural modification. Virtual modifications can be attempted by using QSAR (Quantitative SAR) models to predict specific characteristics prior to synthesizing the compound. In any case, lead optimization can be difficult due to the large number of characteristics to optimize.
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


