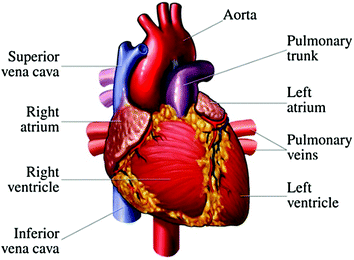
Fig. 2.1
The simplified human circulatory system (Harrub 2005). Oxygenated blood (red) and deoxygenated blood (blue)
The heart is the primary organ in the human body; we cannot live without the heart. Although the heart is “just” a pump that makes the blood circulate in the body, the heart is nevertheless a complex and important organ. Like all other pumps, it can become clogged, break down, and require repair. This is why understanding how the heart works is critical. The anatomy of the heart is depicted in Fig. 2.2; with some knowledge about one’s heart and what is good or bad for it, one can significantly reduce his/her risk for heart disease (Bianco 2014).
Heart disease is the leading cause of death in the United States. Almost 2,000 Americans die of heart disease each day. This means that every 44 s someone dies of a heart-related issue in the USA. On the other hand, the good news is that the heart disease death rate has been steadily falling. Unfortunately, heart diseases are still a reason for sudden death and many people die before even reaching the hospital (Bianco 2014).
2.1.1.1 The Baroreceptor Reflex
The baroreceptor reflex is the most powerful mechanism in the control of systemic arterial pressure. The baroreceptors are spray-type nerve finishes in the walls of the carotid sinus and the aortic arch. The impulse rate of the baroreceptors is an exact image of the transmural pressure. The transmural pressure is the difference in pressure between two sides of a wall or an equivalent separator.
The firing rate increases during systole and decreases during diastole; therefore, the mean firing rate increases with mean arterial pressure. Moreover, the faster the pressure changes, the greater the response of the baroreceptors. In the absence of arterial baroreceptors, the mean arterial pressure would be higher and there would be large variations around the mean value (Timischl 1998).
2.1.1.2 Control of Local Blood Flow
The control of local blood flow is an important mechanism of the circulatory system. Each tissue has the capability to control its own local blood flow according to its demand. Certain vessels, especially arteries in the brain and kidneys, can adjust their resistance so that the blood flow stays almost constant if the blood pressure changes. This mechanism is called the Bayliss effect or myogenic auto-regulation.
Another important mechanism of blood flow control is metabolic auto-regulation, which exists in the small arterioles. If the metabolic rate increases or if less oxygen exists, different chemical substances (a “metabolic cocktail”) are released which cause vasodilation of the small arterioles. Thus, the blood flow is increased and consequently, on the one hand, more nutrients per time are carried to the tissues, and, on the other hand, more unnecessary waste products are removed from the tissues (Timischl 1998).
2.1.1.3 Frank-Starling Mechanism and the Bowditch Effect
The pumping capability of the heart depends upon contractility, pre-load and heart rate (HR). The entire heart can increase its contractility with the help of three mechanisms: the Frank-Starling mechanism, the Bowditch effect, and sympathetic activation.
(a)
The Frank-Starling mechanism refers to the intrinsic capability of the heart to adjust to changing loads of inflowing blood. The heart pumps all the blood that comes into the aorta. For instant if pre-load and force are increased, so in this way increased stroke volume (SV) and pumped against the unchanged aortic pressure. One of the most important effects of the Frank-Starling mechanism is that changes in the arterial pressure against which the heart pumps (=afterload) have almost no effect on SV. If everything else remains constant, SV increases with increased afterload and vice versa. Afterload influences SV by affecting the velocity of contraction (“force-velocity relationship”) (Timischl 1998; Patterson et al. 1914).
(b)
The Bowditch effect is reported as the sensitivity of the cardiac muscle to the interval between contractions. The vigour of the contractions increases if the heart rate increases. The reason is that the interval between heartbeats influences the quantity of calcium available to the force-velocity relationship (Timischl 1998; Patterson et al. 1914; Franz et al. 1983).
(c)
The sympathetic nervous system increases the heart rate (HR) and contractility.
2.1.2 The Respiratory Centre
Strictly speaking, the respiratory centre is not part of the CVS, but it plays an important role closely related to that of the CVS.
The respiratory centre is situated in the medulla oblongata1 and pons; it contains various broadly dispersed groups of neurons. The so-called vagal and glossopharyngeal nerves transmit sensory signals into the respiratory centre from the peripheral chemoreceptors, the baroreceptors, and from different types of receptors in the lungs. The respiratory centre is also closely related to the vasomotor activity.2 Nearly any cause that increases the degree of vasomotor activity also increases, at least moderately, respiration. The neurons in the respiratory centre make the rhythm of respiration and transmit nervous signals to the inspiratory muscles (Timischl 1998).
The overall level of respiratory centre activity is controlled based on the ventilation (i.e. breathing) needs of the body. It is the ultimate goal of respiration to uphold proper concentrations of carbon dioxide, hydrogen ions and oxygen in the body fluids. This is achieved, on the one hand, via feedback that makes the respiratory centre react to changes in the chemical composition of the blood, and, on the other hand, by excitatory signals from other parts of the nervous system that control the respiratory activity (Timischl 1998).
2.2 Models of the Cardiovascular System
Given the complexity of the cardiovascular system (CVS), it would be beneficial to model it for simulation purposes, for example. Thus, developing computational models of the CVS has caught the interest of many researchers over the past decades. What follows summarizes the main developments undertaken since the 50 s to model the CVS.
2.2.1 From Physiology to Mathematical Representation of the CVS
The past has witnessed concentrated re-examination of the concepts related to cardiac output regulation (Grodins 1959).
Controversies have arisen, some real and some only apparent. These controversies served to focus and emphasize the requirement for a basic integration of cardiovascular dynamics.
In 1959, Grodins (Grodins 1959) developed a CVS model based on electrical circuit components. He started with the ventricles, later added a pulmonary circuit, and lastly added a systemic circuit to achieve a closed-loop model with fourteen parameters.
Later in 1963, Defares, Osborne, and Hara (Defares et al. 1963) developed a simple circulation model with six compartments. Each compartment was modelled as a capacitor connected to a ground and to the two end-to-end nodes by impedances; current (flow) through the ventricular compartments was regulated by diodes representing valves. Furthermore, Defares and his colleagues applied their model using discrete analogue components to develop an electrical circuit analogue computer for simulating haemodynamics with real-time behaviour grossly similar to that observed in vivo in humans.
In 1978, Katz and colleagues (Katz et al. 1978) were able to create a real-time digital simulator that was very simple. The co-called Windkessel model was programmed in the FORTRAN program language; it was run on a PDP-12 with output via D/A converters to a polygraph recorder. Thanks to the superior flexibility afforded by digital computer programs over analogue circuit models, it allowed students to vary parameters such as heart rate (HR), stroke volume (SV), total peripheral resistance (TPR), compliance, and valve competence numerically.
In 1982, Campbell and colleagues (Campbell et al. 1982) implemented a CVS model of canine haemodynamics with a five-compartment closed; they used a Hewlett-Packard 1000 computer equipped with an XY plotter. This model was similar to that of Defares; then in the model they incorporated time-varying capacitances, which had already been performed by Suga and Sagawa (Sunagawa and Sagawa 1982); the model ran noticeably slower than real time on the available hardware, because of the complexity of the model.
2.2.2 Structure of the Cardiovascular Model
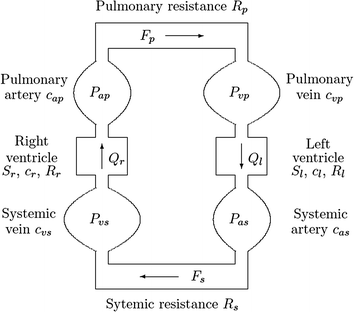
In the study by Timischl (Timischl 1998), the developed part of the cardiovascular model contains two circuits (systemic and pulmonary). Both circuits are placed in series and include two pumps (left and right ventricles); this configuration is depicted in Fig. 2.3.
A fixed blood volume V0 is circulated between the systemic and pulmonary arteries and the systemic and pulmonary veins. The pumps and the resistance vessels are expected to represent an unimportantly small volume.
In (Timischl 1998), the cardiac circle event is ignored and it is assumed one-way and non-pulsatile blood flow by the left and right ventricles. Therefore, during a steady state, the left and right cardiac outputs Ql and Qr, respectively, along with the blood pressures Pas (systemic arterial), Pvs (systemic venous), Pap (pulmonary arterial), and Pvp (pulmonary venous) in different part of the circuits are fixed. Their values represent the respective mean values over the length of a pulse (Timischl 1998; Kappel and Peer 1993).
2.2.2.1 The Mass Balance Equations
In her study (Timischl 1998), Timischl derived a continuity equation for each of the four compartments, which are the systemic artery, the systemic vein, the pulmonary artery, and the pulmonary vein. The variation of blood volume controls the systemic artery, which is the deviation between inflow (Ql) and outflow from systemic flow (Fs). This phenomenon is depicted in Fig. 2.3.
2.2.2.2 The Dependence of Ventricle Output on the Blood Pressures
During the time of steady state, the left cardiac output (Ql) is fixed and it is determined as the mean blood flow over the length of a pulse.
The arterial and venous blood pressures depend upon the cardiac outputs. In turn, the cardiac outputs depend upon the blood pressures. To develop these relationships, the venous filling pressure, the arterial load pressure (pressure opposing ejection of the blood) and the heart rate are considered constant inputs, which can be set arbitrarily. In this way, the impact of each of them on the cardiac output and ventricular volumes can be analysed (“isolated heart”).
In the study by Timischl (Timischl 1998), the objective was to derive the dependence of the stroke volume (Vstr) on the venous (filling) pressure and the arterial (load) pressure.
2.2.2.3 Hagen-Poiseuille’s Law
It is presumed that blood is a homogeneous fluid; its flow depends on the forcing pressure difference and on the opposing viscous resistance via Hagen-Poiseuilles’ law (Timischl 1998). For a model considering the dependence of resistance on blood pressure, metabolic auto-regulation is taken into account when modelling exercise. Up to now, by regarding Rs and Rp as parameters, the resistance vessels are modelled as unbending tubes (Timischl 1998).
2.3 Overview of the Existing CVS Simulator and Software Tools for EBI
Many researchers are working on modelling and simulation in the area of biomedical engineering. Three relevant examples for my work are discussed below. These selected simulator and software tools are focused on cardiovascular simulation (this provides a general basis on how to structure and implement such a simulator) and on thoracic electrical bio-impedance (these provide valuable insight related to the effects of artefacts and estimation errors in EBI measurement and simulation).
2.3.1 Cardiovascular Simulator (CVSim) (Developed at MIT)
CVSim (Heldt et al. 2010) was initially aimed at teaching purposes, but it has subsequently also been used for research purposes.
In this work, inspiration was gained from CVSim to develop a novel simulator (tool) for the EBI signal that could be used as a research tool to model and simulate bio-impedance signals, mainly cardiac and respiratory signals, to subsequently evaluate the performance of signal processing algorithms. It could also be used for teaching and training purposes for engineering and medicine students. More details about the simulator developed in this work are discussed in Sect. 4.3, Chap. 4.
The first version of the cardiovascular simulator (CVSim) was developed in 1983 by Robert Sah based on Defares’ model, and is similar to that of Campbell. Both models are discussed above in Sect. 2.2 of this chapter. Figure 2.4 depicts the six-compartment circuit model, which is introduced by CVSim.
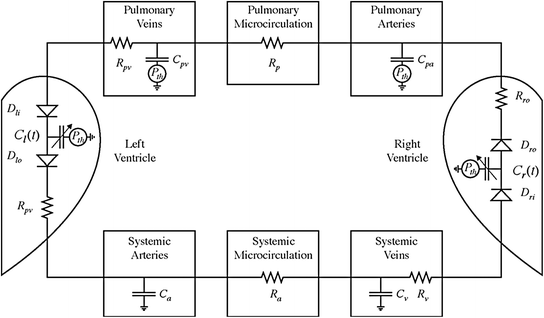

Fig. 2.4
Six-compartment circuit model (Heldt et al. 2010). Counter-clockwise blood flow (electrical current) is driven by contraction of the ventricles (time-varying capacitors)
The two compartments represent the left and right ventricles utilizing time-varying capacitors joined via diodes representing heart valves. The other four compartments relate to the systemic and pulmonary arteries and veins, modelled utilizing linear capacitors and resistors representing the compliance and resistance of the vasculature fragments (Heldt et al. 2010).
In the beginning, CVSim was considered only for teaching and training purposes. Beginning in the late 1990s, Thomas Heldt and Eun Bo Shim – and, individually, Ramakrishna Mukkamala – adapted CVSim for research uses. It is a lumped-parameter model of the human CVS that has been built and applied for research purposes, as well as for teaching quantitative physiology courses at MIT and Harvard Medical School since 1984 (Heldt et al. 2010).
The CVS model is established on realistic parameter values indicating normal human physiology and contains the main arterial baroreflex system for blood pressure homeostasis. The graphical user interface (GUI) allows easy and intuitive interaction with the model. It is capable of simulating pulsatile blood pressures, volumes, and flow rates whose mean, systolic, and diastolic values are within the normal ranges of an adult human (Heldt et al. 2010).
2.3.1.1 Application
Teaching: CVSim has been employed since 1984 for teaching and training the lumped-parameter cardiovascular model to engineering students at MIT and medical students.
Research: In research, CVSim has been extended in various ways. These may be categorized as either the development and assessment of novel algorithms, or the study of cardiovascular responses to physiologic perturbations.
The Research CardioVascular SIMulator (RCVSIM) has been effectively used to build and assess system identification algorithms for evaluating transfer functions and parameters that describe the main cardiovascular regulatory mechanisms (e.g. baroreflex (BRR), control of heart rate (HR) and total peripheral resistance (TPR)), and haemodynamic parameters (maximal ventricular elastance changes) from non-invasive measurements of beat-to-beat cardio-respiratory variability (Chen et al. 2008; Lu and Mukkamala 2004, 2005; Mukkamala and Cohen 2001; Mukkamala et al. 2003).
The benefit of applying a cardiovascular simulator for this aim is that the real reference values of the quantities required for assessment are precisely known. Independent reference measurements in an experimental model may be difficult or even impossible in the case of a transfer function (Heldt et al. 2010).
2.3.2 Software Tool for Analysis of Breathing-Related Errors in Transthoracic Electrical Bio-Impedance Spectroscopy Measurements (EBSM) (Developed at KTH, UB and KI, Sweden and Philips, Netherlands)
In this study (Abtahi et al. 2012), the authors focused on developing a software tool (Fig. 2.5) that can be employed to simulate the influence of respiration activity in frequency-sweep EBSM of the human thorax to examine the effects of the different sources of error. The helpfulness of the software tool is showcased by an example of deviations and errors gained in estimation of Cole parameters. The impedance of respiration is only modelled as a sinusoid with its amplitude controlled by an end-user to simulate spectrum measurements which are not synchronized with respiration cycle.
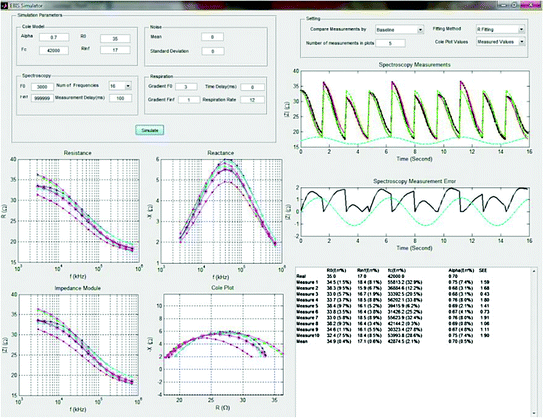

Fig. 2.5
GUI of the developed software tool for Electrical Bio-impedance Spectroscopy Measurements (EBSM) (Abtahi et al. 2012)
The application of the tool has helped the authors to affirm their hypothesis that the measurement time delay caused by sweeping between frequencies on the acquisition of EBIS measurements influences the measured spectrum, generating a measurement artefact, and accordingly taints any subsequent data analysis using Cole parameter classifications.
2.3.3 Simulation of Lung Edema in Impedance Cardiography (Developed at Philips, Germany and Netherlands)
In (Ulbrich et al. 2012), the aim was to recognize the causes for inaccuracy of the ICG in assessing the SV for heart failure patients. Thus, simulations using a finite element model (FEM) examined the effect of lung edema on the ICG.
The simulation model is based on human MRI data, along with volumetric variations of the heartbeat and aortic expansion, as well as variations during lung perfusion and erythrocyte orientation.
2.4 Acquiring Physiological Information from the Cardiovascular System
In medicine, an extensive variety of procedures, tests, and tools are already available for diagnosing and treating cardiovascular disease. Some of these procedures are very simple to use on patients, some of them are very difficult, whilst others are not only difficult but also very risky for the patients.
In a very wide and general sense, such procedures can be divided into invasive procedures and non-invasive procedures.
Invasive procedures are medical procedures that break or penetrate the skin, via catheterization or other ways of entering a body cavity. This is a large category and contains just about all major surgeries and many diagnostic tests. If it leaves a mark, it is most probably an invasive procedure.
Non-invasive procedures are also medical procedures that are very common. These procedures do not need to break the skin. Simple examples include inspecting the inside of the nose and performing a check-up of the eardrum. However, more advanced or complicated procedures can also be performed non-invasively.
Non-invasive procedures comprise a large category including methods such as imaging studies, together with x-rays, ultrasound, MRI, and CT scans. ECGs also fall under the non-invasive category. Some of these procedures are not only for making a good diagnosis; they are also used for treatment of patients. For instance, radiotherapy is used to treat cancer patients. In this procedure, a simple radiation is applied to the particular area of the patient’s body in order to kill a cancerous tumour. In this procedure, it is not required to break the patient’s skin, as the radiation beam can be applied from the outside (Rosenberger 2009). The literature reports on the various studies that took place to compare invasive and non-invasive methods; more details can be found in e.g. Jurjević et al. 2009 and Soudon et al. 2008.
2.4.1 Need for Non-invasive Methods
The aim of non-invasive methods is to minimize the required cost and hospitalization time, as well as to increase patient ease and safety (Solà et al. 2011). The ECGs, intermittent blood pressure (BP) monitors, and pulse oximeters have been successfully released into the market, paving the way towards the monitoring of cardiac and vascular parameters in hospitals and out-patients (Parati et al. 2008).
The non-invasive electrical-based methods are of special interest because these are mostly simple, safe, and inexpensive means of assessing haemodynamic parameters. The following lists the most relevant ones and their respective use related to cardiac diseases.
(a)
Electrocardiogram (ECG) is a record of the electrical activity of the heart. The sensors detect electrical impulses coming from the heart, where the heart muscle contracts. ECG is normally used to detect abnormal heart rhythms and to inquire as to the cause of chest pains (Kenny and Tidy 2012).
(b)
Opto–Electronic Plethysmography (OEP) is a relatively novel technique to assess the ventilation pattern by an external measurement of the chest wall surface motion. The OEP system measures variations in the complex shape of the chest wall while breathing by modelling the thoracoabdominal surface with a large number of points belonging to chosen anatomical reference sites of the rib cage and abdomen (Santos et al. 2013).
(c)
Electrical Impedance Tomography (EIT) is monitoring technology based on the analysis of multiple bio-impedance signals. From an electrical perspective, the thoracic cavity is composed of distributed impedance volumes. While the lungs are filled with air, they form high impedance volumes, whereas the heart and blood vessels, filled with blood, form volumes with lower impedance (Solà et al. 2011).
(d)
Impedance Cardiography (ICG) measurement has been offered as a cost-effective non-invasive method for monitoring haemodynamic parameters. The time-variant part of the bio-impedance (BI) phasor reflects processes in the patient’s physiological state, since some changes in BI can be caused by normal activity or pathological reasons (Grimnes and Martinsen 2014; Mughal 2014). Extracting information from impedance signals for diagnosing diseases and assessing heart function is essential for exploiting this method (Mughal et al. 2015).
(e)
Foucault Cardiography (FCG) is a method for monitoring the cardio-haemodynamic cases of the cardiac region of the thorax with the eddy currents induced in it using radio-frequency magnetic field. The measurable signal is acquired because of the variation in the power absorbed by the tissues, along with the variation of their electrical impedance (Trolla and Vedru 2001).
(f)
Electro–mechanical Wave Imaging (EWI) is an entirely non-invasive, non-ionizing, ultrasound-based imaging method. It is based on mapping the electro-mechanical activation sequence of the myocardium along various echocardiographic planes. EWI is capable of detecting and mapping the electromechanical contraction wave (Kohl et al. 2011).
From the measured data (obtained by means of one or several of the above procedures), one can assess physiological activities and structural configurations of a tissue, as well as analyse dynamic processes in organs such as the heart and lungs.
Data measurement plays a key role in measurement of the stroke volume (SV) of the heart, cardiovascular system, and many other parameters, as described by Cotter et al. (2006).
The six non-invasive bioelectrical methods listed above have their own merits and limitations. Still, one key problem shared by all of them is that of the measurement and useful signal extraction. In particular, there exist uncertainties regarding the properties of the signals, such as amplitude, waveform, components (e.g. cardiac vs. respiration), and the origin of the signal waveform (e.g. is it due to configuration/positioning of electrodes/sensors or the condition of the patient). This, in turn, limits the quality of the diagnostics for diseases and conditions.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree