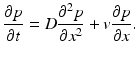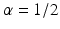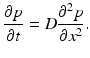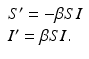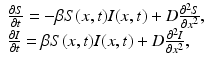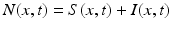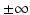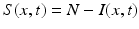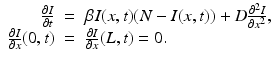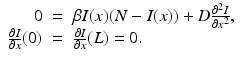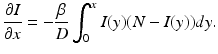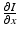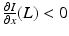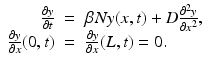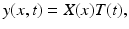(1)
Department of Mathematics, University of Florida, Gainesville, FL, USA
15.1 Introduction
Classical epidemic models assume that the entire population lives in one area and is well mixed. That assumption is not necessarily satisfied. For instance, the population may be living on isolated islands or in different countries while traveling from one location to another. This spatial heterogeneity affects the transmission of the disease. To understand the precise impact of spatial heterogeneity on the dynamics of a disease, we have to build models that account for that heterogeneity. Spatially explicit models are also more effective in evaluating control strategies, particularly those applied to movement of individuals.
Multiple modeling approaches have been used to account for space and movement of individuals in epidemic models. Space can be incorporated as a variable in discrete or continuous form. One of the most popular discrete-space modeling approaches is the metapopulation approach [16, 52, 102]. We will introduce the metapopulation approach in the next section. Other discrete space modeling approaches include epidemic spatial networks [20, 21, 43, 123], cellular automata [101, 147], and lattice epidemic models [137, 141]. Continuous space models include diffusion epidemic models [34, 82, 156], integrodifferential equation epidemic models [116, 136] and integrodifference equation epidemic models [8].
In this chapter, we will focus on metapopulation models and diffusion models as two types of modeling techniques incorporating movement of individuals. Each of these model types requires a different mathematical tool. Metapopulation models typically represent a large system of ordinary differential equations. Diffusion epidemic models, on the other hand, are small systems of partial differential equations.
15.2 Metapopulation Modeling of Epidemic Spread
The concept of metapopulation does not originate in epidemiology, but in ecology. A metapopulation [95] is a group of populations of the same species that leave in spatially isolated areas but interact on some level. Metapopulations occur when different populations live in fragmented habitats but are connected through migration. The isolated areas that are occupied by each population are called patches. In epidemiology, patches may be cities, countries, islands, or other geographically autonomous regions. A necessary requirement of a metapopulation is that patches be connected through migration. Migration is defined as physical movement of individuals from one area to another. Movement can be short-term or long-term. In short-term movement, individuals visit another location for a period of time and return to the home patch. Even though the movement is short-term, it still allows an infected individual to transmit the pathogen to a susceptible individual of a different patch, thus spreading the disease to other locations. Long-term migration arises when individuals move to another location and settle there. The two types of movement are modeled differently. Short-term movement has been called Lagrangian movement, and the corresponding models are called Lagrangian metapopulation models. Long-term movement has been called Eulerian movement, and the corresponding models are called Eulerian metapopulation models [44].
Metapopulation epidemic models consist of n patches. The population of each patch is assumed to be homogeneously mixing. It is divided into the typical epidemiological classes of susceptibles, infectives, and other classes. The sizes of each of these classes are different on different patches. Individuals of some or all of the classes travel between the patches, which leads to the movement of the disease (Fig. 15.1).
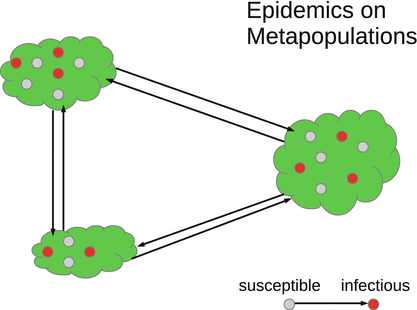

Fig. 15.1
Schematic representation of a metapopulation epidemic model
Historically, early metapopulation epidemic models incorporated short-term movement between the patches. Correspondingly, we begin by describing the Lagrangian modeling framework in the next subsection. Later, Eulerian models were developed, in which the movement is explicit and occurs at certain rates. We will consider an Eulerian modeling framework in the second subsection of this section.
15.2.1 Lagrangian Movement Epidemic Models
We begin by assuming that the total population occupies n regions or patches. The population of patch i is denoted by N i , and the total population size is 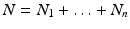 . The population of the ith region is infected by a pathogen and consists of S i susceptible individuals, I i infected individuals, and R i recovered/immune individuals. We have
. The population of the ith region is infected by a pathogen and consists of S i susceptible individuals, I i infected individuals, and R i recovered/immune individuals. We have 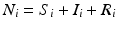 . In terms of movement, we assume that the members of each region make short visits to at least some of the other regions and return to their home patch. Furthermore, we shall make the simplifying assumption that all members of each region spend the same amount of time visiting other regions, but that time depends on the visited region. While commuting to other regions, infected visitors can transmit the disease to susceptibles in the visited region, while susceptible visitors can acquire the disease from infected members of the visited region. Long-term migration of the members of this community will not be incorporated in this model. Furthermore, we assume for simplicity that the population size of each region remains constant, that is, births μ i N i are balanced by deaths, where μ i is the death rate in region i. With these assumptions, the model takes the form
. In terms of movement, we assume that the members of each region make short visits to at least some of the other regions and return to their home patch. Furthermore, we shall make the simplifying assumption that all members of each region spend the same amount of time visiting other regions, but that time depends on the visited region. While commuting to other regions, infected visitors can transmit the disease to susceptibles in the visited region, while susceptible visitors can acquire the disease from infected members of the visited region. Long-term migration of the members of this community will not be incorporated in this model. Furthermore, we assume for simplicity that the population size of each region remains constant, that is, births μ i N i are balanced by deaths, where μ i is the death rate in region i. With these assumptions, the model takes the form
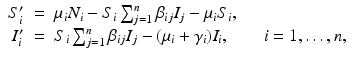
where we have omitted the equations for the recovered. Here, γ i represents recovery in the ith patch, and β ij are the transmission rates of infected individuals from patch j to susceptible individuals in patch i. We note again that since we are assuming constant population size in each region, the birth rate equals the death rate. In addition, if we add the equations for S i , I i , and R i , we obtain the following differential equation for the population size of patch i: N i ′ = 0.
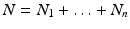 . The population of the ith region is infected by a pathogen and consists of S i susceptible individuals, I i infected individuals, and R i recovered/immune individuals. We have
. The population of the ith region is infected by a pathogen and consists of S i susceptible individuals, I i infected individuals, and R i recovered/immune individuals. We have 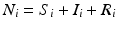 . In terms of movement, we assume that the members of each region make short visits to at least some of the other regions and return to their home patch. Furthermore, we shall make the simplifying assumption that all members of each region spend the same amount of time visiting other regions, but that time depends on the visited region. While commuting to other regions, infected visitors can transmit the disease to susceptibles in the visited region, while susceptible visitors can acquire the disease from infected members of the visited region. Long-term migration of the members of this community will not be incorporated in this model. Furthermore, we assume for simplicity that the population size of each region remains constant, that is, births μ i N i are balanced by deaths, where μ i is the death rate in region i. With these assumptions, the model takes the form
. In terms of movement, we assume that the members of each region make short visits to at least some of the other regions and return to their home patch. Furthermore, we shall make the simplifying assumption that all members of each region spend the same amount of time visiting other regions, but that time depends on the visited region. While commuting to other regions, infected visitors can transmit the disease to susceptibles in the visited region, while susceptible visitors can acquire the disease from infected members of the visited region. Long-term migration of the members of this community will not be incorporated in this model. Furthermore, we assume for simplicity that the population size of each region remains constant, that is, births μ i N i are balanced by deaths, where μ i is the death rate in region i. With these assumptions, the model takes the form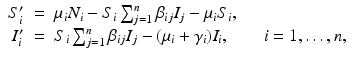
(15.1)
We obtain the disease-free equilibrium: 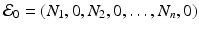 . If we imagine that commuting between patches does not occur, that is, if β ij = 0 for i ≠ j, then we can define a reproduction number for each patch:
. If we imagine that commuting between patches does not occur, that is, if β ij = 0 for i ≠ j, then we can define a reproduction number for each patch:
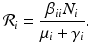 If
If 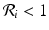 , then the disease will disappear in patch i if it is isolated from the metapopulation. If
, then the disease will disappear in patch i if it is isolated from the metapopulation. If ![$$\mathcal{R}_{i} > 1$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_15_Chapter_IEq5.gif”></SPAN>, then the disease will persist in patch <SPAN class=EmphasisTypeItalic>i</SPAN> if it is isolated from the metapopulation.</DIV><br />
<DIV id=FPar1 class=]()
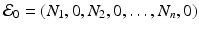 . If we imagine that commuting between patches does not occur, that is, if β ij = 0 for i ≠ j, then we can define a reproduction number for each patch:
. If we imagine that commuting between patches does not occur, that is, if β ij = 0 for i ≠ j, then we can define a reproduction number for each patch: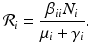
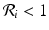 , then the disease will disappear in patch i if it is isolated from the metapopulation. If
, then the disease will disappear in patch i if it is isolated from the metapopulation. If Definition 15.1.
We call patch i a sink if 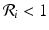 . We call patch i a source if
. We call patch i a source if 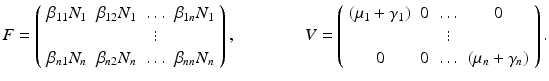
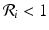 . We call patch i a source if
. We call patch i a source if 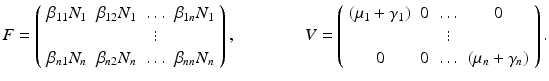
(15.2)
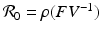 , where
, where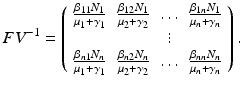
(15.3)
 , and we consider the Jacobian of system (15.1). It takes the form
, and we consider the Jacobian of system (15.1). It takes the form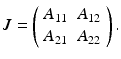
(15.4)
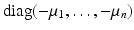 . The matrix A 22 is given by
. The matrix A 22 is given by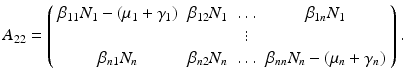
(15.5)
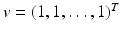 . Then the condition − A 22 v > 0 is equivalent to the following conditions being satisfied:
. Then the condition − A 22 v > 0 is equivalent to the following conditions being satisfied:(15.7)
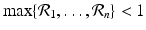 , so in this case, all patches must be sinks. However, if even one patch is a source, that is, if there exists j 0 such that
, so in this case, all patches must be sinks. However, if even one patch is a source, that is, if there exists j 0 such that 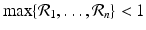 .
.15.2.2 Eulerian Movement Epidemic Models
To formulate the Eulerian movement epidemic model, we assume that the population lives on n patches. In Eulerian movement, it is assumed that individuals move to another patch and settle there, becoming a part of the population of the host patch. Further, we assume that within each patch, the population mixes homogeneously and the distribution of the disease is described by a classical SIR endemic model. We denote the migration rates from patch j to patch i by m ij . We assume m ii = 0. Furthermore, the migration rates of susceptible and infective may be different, so the m ij S denote the migration rates of susceptibles, and the m ij I denote the migration rates of infectives. A more complex model of this form was considered in [17]:
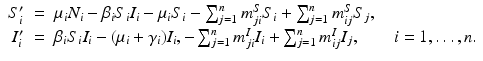
In the above model, we have once again omitted the equation of the recovered. The total birth/recruitment rate into patch i is μ i N i , the mortality rate in patch i is μ i , the transmission rate in patch i is β i , and the recovery rate in patch i is γ i . The total population size is given by 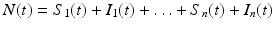 , and it satisfies the differential equation
, and it satisfies the differential equation
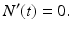 Hence, the total population size remains constant.
Hence, the total population size remains constant.
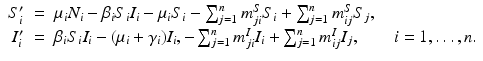
(15.8)
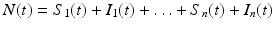 , and it satisfies the differential equation
, and it satisfies the differential equation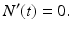
To find the disease-free equilibrium, let I i = 0 for 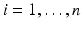 . The disease-free equilibrium is given by
. The disease-free equilibrium is given by 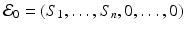 . Then the disease-free equilibrium satisfies the following system of equations:
. Then the disease-free equilibrium satisfies the following system of equations:
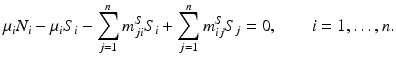
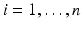 . The disease-free equilibrium is given by
. The disease-free equilibrium is given by 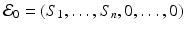 . Then the disease-free equilibrium satisfies the following system of equations:
. Then the disease-free equilibrium satisfies the following system of equations: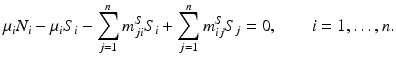
We rewrite this system in the form
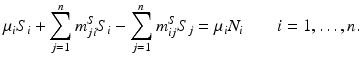 The matrix of this system is
The matrix of this system is
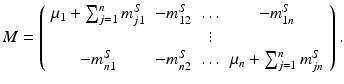
The matrix M possesses the Z-pattern. Furthermore, for 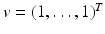 , M T v > 0. Hence, M is an M-matrix. As a result, it has a nonnegative inverse, and therefore the system has a nonnegative solution. We conclude that there is a unique nonnegative disease-free equilibrium.
, M T v > 0. Hence, M is an M-matrix. As a result, it has a nonnegative inverse, and therefore the system has a nonnegative solution. We conclude that there is a unique nonnegative disease-free equilibrium.
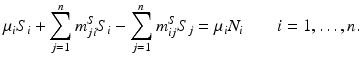
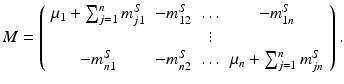
(15.9)
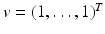 , M T v > 0. Hence, M is an M-matrix. As a result, it has a nonnegative inverse, and therefore the system has a nonnegative solution. We conclude that there is a unique nonnegative disease-free equilibrium.
, M T v > 0. Hence, M is an M-matrix. As a result, it has a nonnegative inverse, and therefore the system has a nonnegative solution. We conclude that there is a unique nonnegative disease-free equilibrium.To compute the reproduction number, we use the next-generation approach. The infective variables are 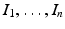 . We compute the matrices F and V. The new infections are given by the incidence terms. Hence
. We compute the matrices F and V. The new infections are given by the incidence terms. Hence 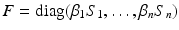 . All remaining terms give V:
. All remaining terms give V:
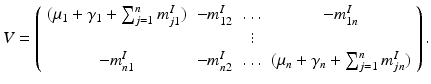
The reproduction number is then defined as 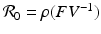 . It follows from the results in [159] that if
. It follows from the results in [159] that if 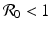 , the disease-free equilibrium is locally asymptotically stable, and if
, the disease-free equilibrium is locally asymptotically stable, and if 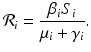
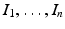 . We compute the matrices F and V. The new infections are given by the incidence terms. Hence
. We compute the matrices F and V. The new infections are given by the incidence terms. Hence 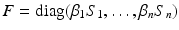 . All remaining terms give V:
. All remaining terms give V: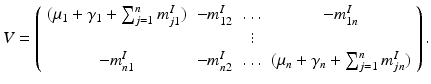
(15.10)
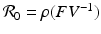 . It follows from the results in [159] that if
. It follows from the results in [159] that if 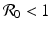 , the disease-free equilibrium is locally asymptotically stable, and if
, the disease-free equilibrium is locally asymptotically stable, and if 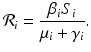
(15.11)
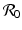 computed by the next-generation approach is bracketed between the two patch reproduction numbers.
computed by the next-generation approach is bracketed between the two patch reproduction numbers.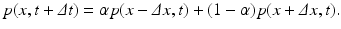
![$$\displaystyle\begin{array}{rcl} \frac{p(x,t +\varDelta t) - p(x,t)} {\varDelta t} & =& \frac{1} {2\varDelta t}[p(x -\varDelta x,t) - 2p(x,t) + p(x +\varDelta x,t)] \\ & & +\frac{1/2-\alpha } {\varDelta t} [p(x +\varDelta x,t) - p(x -\varDelta x,t)].{}\end{array}$$](/wp-content/uploads/2016/11/A304573_1_En_15_Chapter_Equ12.gif)
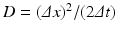
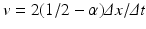
![$$\displaystyle\begin{array}{rcl} \frac{p(x,t +\varDelta t) - p(x,t)} {\varDelta t} & =& D\left [\frac{p(x -\varDelta x,t) - 2p(x,t) + p(x +\varDelta x,t)} {(\varDelta x)^{2}} \right ] \\ & & +v\left [\frac{p(x +\varDelta x,t) - p(x -\varDelta x,t)} {2\varDelta x} \right ]. {}\end{array}$$](/wp-content/uploads/2016/11/A304573_1_En_15_Chapter_Equ13.gif)