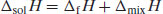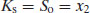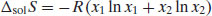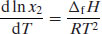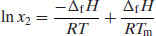The concentration of drug dissolved at this point is known as the equilibrium solubility (usually the term solubility is used alone) and the solution is saturated. If the drug has an ionisable group then the equilibrium solubility of the un-ionised form is called the intrinsic solubility (So). This is important, because if the drug is ionisable it will ionise to a greater or lesser extent with solution pH and this will affect the observed solubility, as discussed in Chapter 2. If the structure of the compound is known, then it should be clear whether solubility will exhibit a dependence upon pH. If the structure is not known then measuring solubility over a range of pH will show whether an ionisable moiety is present (although care must be taken when selecting the buffer to ensure salts are not accidentally formed). If the compound has an ionisable group, then modification of solubility by preparation of a salt is a possible formulation strategy (see Chapter 6).
From a thermodynamic perspective, the energy input required in order to break any solute–solute interactions must be equal to the enthalpy of fusion required to melt the solid (since the same interactions must be overcome). Unlike melting, however, in the case of dissolution there is an additional change in enthalpy where solvent–solvent intermolecular interactions are broken and solute–solvent interactions are formed, termed the enthalpy of mixing (ΔmixH). The net enthalpy of solution (ΔsolH) is then the sum of the enthalpies of fusion and mixing:
The overall process of dissolution can be represented more simply as
(4.3)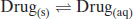
In this case the equilibrium constant (K) can be written as
(4.4)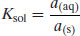
where a denotes the activity of the drug in each phase. Since the activity of a solid is defined as unity and activity approximates to concentration (saturation in this case) in dilute solution then
where x2 denotes the saturated concentration of drug in mole fraction units (x1 being the mole fraction of the solvent). It should now be possible to see from Equation (4.5) the reason for the term equilibrium solubility noted earlier.
It appears from Equation (4.2) that the crystal lattice energy might affect solubility. It also seems from Equation (4.1) that there should be an effect of temperature on solubility, since the position of equilibrium will change. Both of these effects can be explored further through the concept of ideal solubility.
- Solubility is the maximum concentration of a given solute that can be attained in a given solvent.
- Solids transition to solution by dissolution.
- Thermodynamic solubility is a position of equilibrium.
- Dissolution governs the rate at which solubility is achieved.
- As a general rule, solubility below 1 mg mL−1 is likely to hinder development while solubility above 10 mg mL−1 is acceptable.
4.2.1 Ideal solubility
In the special case where the enthalpy of any solute–solvent interaction is equal to the enthalpy of any solvent–solvent interaction then solvation of the solute may occur with no change in enthalpy (i.e. ΔmixH = 0) and dissolution is said to be ideal. Formation of an ideal solution also occurs with the following change in entropy (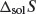 ):
):
where R is the universal gas constant (8.314 J K−1mol−1). Ideal dissolution (although unlikely, because the solute and solvent molecules would need to possess identical properties, such as size, shape and chemical nature) leads to ideal solubility and is an interesting theoretical position because it can be described in thermodynamic terms, which allows calculation of the dependence of solubility on temperature.
From Equation (4.2) if ΔmixH = 0 then ΔfH is equal to ΔsolH (note that since ΔfH must be positive, i.e. endothermic, ΔsolH must also be positive for ideal dissolution). For a process to occur spontaneously the Gibbs free energy (ΔG) must be negative. The familiar thermodynamic relationship for dissolution is
(4.7)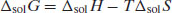
where T is absolute temperature. ΔsolG is most likely to be negative when ΔsolH is negative but, as noted above, ΔsolH is frequently positive for dissolution and must be so when dissolution is ideal. This means that for dissolution to occur spontaneously the driving force can only be a significant increase in entropy. Since the mole fractions of both solvent and solute must be less than 1, the logarithmic terms in Equation (4.6) must be negative and so the change in entropy must be positive, which agrees with this argument.
Equation (4.5) shows that solubility is a position of equilibrium and thus has the attributes of an equilibrium constant. If so, it is possible to apply the van’t Hoff equation, yielding
Assuming that ΔfH is independent of temperature (in effect, ignoring any change in heat capacity) then integrating Equation (4.8) from Tm to T results in
where Tm is the melting temperature (usually the extrapolated onset temperature of melting, as melting typically occurs over a range of 1–2 °C) of the pure drug substance and T is the experimental temperature. Equation (4.9) is very useful, since it allows prediction of ideal solubility at any particular temperature so long as the melting temperature and enthalpy of fusion of the pure drug substance are known (both are easily determined from a DSC measurement).
Example 4.1 The melting temperature of aspirin is 137 °C and its enthalpy of fusion at the melting temperature is 29.80 kJ mol−1. What is the ideal solubility of aspirin at 25 °C?
Applying Equation (4.9),
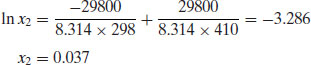
Of course, real solutions invariably do not show ideal behaviour, because the assumptions made above that ΔmixH = 0 and that effects of heat capacity can be ignored are not always valid. A negative (exothermic) enthalpy of mixing increases solubility while a positive (endothermic) enthalpy of mixing reduces solubility. Tables 4.3 and 4.4 list the experimentally measured solubilities for aspirin and paracetamol in a range of solvents. Note that solubility in water is by far the lowest of any of the solvents shown, while solubilities in THF and methanol approach ideality in the case of aspirin and exceed ideality in the case of paracetamol. This explains why THF and methanol are frequently used as solvents to aid dissolution of poorly soluble drug substances during preformulation assay development. Methanol, as noted in Chapter 2, is also commonly used as a co-solvent for determination of pKa for poorly soluble compounds.
Table 4.3 Ideal (calculated) solubility for aspirin compared with experimentally determined solubilities in a range of solvents (at 25 °C, assuming MP 137.23 °C, ΔfH 29.8 kJ mol−1) (data from the RSC Open Notebook Science Challenge).
| Solvent | Solubility (mole fraction) |
| Ideal (calculated) | 0.037 |
| THF | 0.036 |
| Methanol | 0.025 |
| Ethanol | 0.023 |
| Acetone | 0.018 |
| Chloroform | 0.015 |
| 1-Propanol | 0.011 |
| Acetonitrile | 0.006 |
| Water | 0.000 45 |
Table 4.4 Ideal (calculated) solubility for paracetamol compared with experimentally determined solubilities in a range of solvents (at 30 °C, assuming MP 170 °C, ΔfH 27.6 kJ mol−1) (data from Granberg and Rasmuson (1999)).
| Solvent | Solubility (mole fraction) |
| Ideal (calculated) | 0.031 |
| Diethylamine | 0.389 |
| Methanol | 0.073 |
| THF | 0.069 |
| Ethanol | 0.066 |
| 1-Propanol | 0.051 |
| Acetone | 0.041 |
| Acetonitrile | 0.009 |
| Water | 0.002 |
The reason for nonideal solubility in so many solvents, water in particular, is because of significant intermolecular interactions resulting from chemical structure and properties. The three primary properties are the dipole moment, dielectric constant and capacity for forming hydrogen bonds.
A molecule has a dipole when there is a localised net positive charge at one end and a localised net negative charge at the other; such molecules are said to be polar. Water is an example of a polar molecule. Drug substances that have dipoles or a dipolar character are generally more soluble in polar solvents. This is an important point to remember during later chapters.3
Dielectric properties are related to the capacity of a molecule to store a charge and are quantified by a dielectric constant. Polar solvents may induce a dipole in a dissolved solute, which will increase solubility. The dielectric constants of a number of commonly used pharmaceutical solvents are given in Table 4.5. It can be seen that water has a high dielectric constant (78.5) relative to methanol (31.5) even though both are considered to be polar solvents.
Table 4.5 Dielectric constants of some common pharmaceutical solvents at 25 °C.
| Solvent | Dielectric constant |
| Water | 78.5 |
| Glycerin | 40.1 |
| Methanol | 31.5 |
| Ethanol | 24.3 |
| Acetone | 19.1 |
| Benzyl alcohol | 13.1 |
| Phenol | 9.7 |
| Ether | 4.3 |
| Ethyl acetate | 3.0 |
Hydrogen bonding occurs when electronegative atoms (such as oxygen) come into close proximity with hydrogen atoms; electrons are pulled towards the electronegative atom creating a reasonably strong force of interaction. A drug substance that has a functional group capable of hydrogen bonding with water (such as –OH, –NH or –SH) should have increased aqueous solubility.
4.2.2 Solubility as a function of temperature
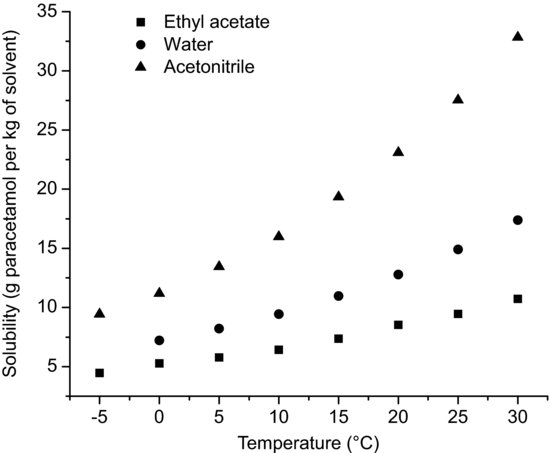
Since ΔfH must be positive, Equation (4.9) suggests that the solubility of a drug should increase with an increase in temperature. Generally, this agrees with everyday experience (Figure 4.1 shows the relationship between solubility and temperature for paracetamol in three solvents), but there are some drug substances (9,3′′-diacetylmidecamycin, for instance; Sato et al., 1981) for which solubility decreases with increasing temperature. This is because the assumption was made in deriving Equation (4.9) that ΔfH was equal to ΔsolH. However, as noted above and as demonstrated by the data in Tables 4.3 and 4.4, ΔmixH is frequently not zero and hence the equality assumed in Equation (4.2) cannot be true. In cases where ΔsolH is negative (i.e. the enthalpy of solution is exothermic) solubility will decrease with increasing temperature. Schematically, these effects are shown in Figure 4.2.
Figure 4.1 Solubility as a function of temperature for paracetamol in three solvents (data from Granberg and Rasmuson (1999)).