Chapter 9
Software for fitting mixed models
In this chapter, we will look at software for fitting mixed models, with a particular emphasis on the SAS package, which has been used to analyse the majority of our examples. In Section 9.1, we mention briefly some of other packages and programs that are available for fitting mixed models. Basic details on the use of the SAS procedure PROC MIXED for fitting normal mixed models are given in Section 9.2. In Section 9.3, we give details on using PROC GENMOD and PROC GLIMMIX for fitting GLMMs, and in Section 9.4, details on PROC MCMC for fitting models using a Bayesian approach.
9.1 Packages for fitting mixed models
There have been very many different programs and software packages developed to implement mixed models or multi-level models. These range from programs to implement a single type of model to comprehensive statistical packages such as SAS. Some are regularly updated to run on the latest versions of operating systems, while others are only available on relatively old operating systems. New products are constantly being introduced to the market, often for a very specific application. As an example, GEMMA is software ‘implementing the Genome-wide Efficient Mixed Model Association algorithm for a standard linear mixed model and some of its close relatives for genome wide association studies (GWAS)’. Further details can be found at (home.uchicago.edu/xz7/software.html). It is impractical to list all of the software available for fitting mixed models, and we will not attempt to try it. We will, however, say a few words about some of the packages available. Inclusion within the following list is not an endorsement of these packages, and neither should the absence of any package be taken as a criticism.
License fees for many of the more comprehensive statistical software packages can be quite expensive, and so it is a wise precaution to ensure that the capabilities match all of a user’s needs and not just those relating to mixed models. For those unable to afford license fees, it is worth mentioning R software. This is free software that is now used widely, but by no means exclusively, in the academic community. The authors of this book are not themselves R users, but some of our colleagues are enthusiastic, particularly about its graphics capabilities. It requires an initial investment of time to learn R but is well worth considering, especially when funding is an issue, though its mixed models capability is not as good as that provided by SAS.
SAS The MIXED and GLIMMIX procedures provide very versatile software for fitting mixed models. They can be used to fit all types of mixed models (random effects, random coefficients and covariance pattern models). In addition, the MCMC procedure may be used to fit mixed models using a Bayesian approach. More details are provided in Sections 9.2–9.4.
Genstat Mixed models for normal data can be fitted using the VCOMP and REML directives, and GLMMs can be fitted using the GLMM directive. In addition, a set of procedures to fit the GLMM models described by Lee and Nelder (1996) is available. These allow the random effects in GLMMs to assume alternative distributions to the normal distribution. The VSTRUCTURE directive can be used to specify covariance patterns. There is not a directive for analysing ordinal data; however, the Biometris GenStat Procedure Library written by members of the Centre for Biometry Wageningen (CBW) contains a suitable procedure, IRCLASS. This procedure library may be freely downloaded from http://www.wageningenur.nl/en/show/Biometris-GenStat-Procedure-Library-Edition-15.htm.
MLwiN MLwiN is a package originally developed by the Multilevel Modelling Project at the Institute of Education in London. It can be used to fit both normal mixed models, GLMMs, and mixed models for ordinal and categorical data. However, the choice of covariance patterns available is more limited than in PROC MIXED. An R command interface to the MLwiN software package is available via software called R2MLwiN. Further information on MLwiN can be found at http://www.bristol.ac.uk/cmm/software/mlwin/.
R R is a free software environment for statistical computing and graphics. Mixed models for normal data can be fitted in using ‘lme4’ and ‘nlme4’ functions. More details on these functions can be found in the textbook ‘Mixed-effects models in S and S-PLUS’ by Pinheiro and Bates (2000) (R functions were originally developed for use within S and S-PLUS). Covariance patterns can be specified using the ‘correlation’ argument. GLMMs can be fitted using the ‘glmm’ or ‘glmmpql’ functions. The ‘glmmpql’ function is discussed in the fourth edition of Modern applied statistics with S, Venables and Ripley (2002); the book also covers normal theory models; and there is online support for the book at www.stats.ox.ac.uk/pub/MASS4/. Interfaces have been written to allow use of both MlwiN and WinBUGS software to be accessed from within R (R2MLwiN and R2WinBUGS). More information on R is available at www.r-project.org.
SPSS Mixed models for normal data can be fitted using the MIXED procedure. GLMMs may be fitted using the GLMM procedure, which is available within the Advanced Statistics software ad-on.
Stata Random effects models may be fitted using the ‘xtmixed’ command. Non-normal mixed models may be fitted within the GLLAMM add-on software (see www.gllamm.org/). The range of available covariance pattern models appears to be more restricted than is available in SAS.
WinBUGS This is a package dedicated to Bayesian analysis using the Gibbs sampler and has been developed by the Medical Research Council Biostatistics Unit in Cambridge. It can be used to fit random effects models to all types of data. The package can be obtained at www.mrc-bsu.cam.ac.uk/bugs. It is free of charge at the time of writing. WinBUGS software may be accessed from R using R2WinBUGS. This writes a data file, input file, and a script, runs the script in WinBUGS, and returns the output simulations to R.
9.2 PROC MIXED
PROC MIXED is a SAS procedure for fitting normal mixed models. It can be used to fit any type of mixed model (random effects, random coefficients, covariance pattern or a combination). It has great flexibility, and there are many options available for defining mixed models and their output. By default, the REML estimation method is applied (see Section 2.2.1). Alternatively, other likelihood-based methods can be applied, and a Bayesian analysis is also available for random effects and random coefficients models (see Section 2.3). Documentation for PROC MIXED is perhaps most easily accessed online during a SAS session. Details are also available from support.sas.com/documentation/onlinedoc. Another excellent text on using SAS to fit mixed models is SAS System for Mixed Models, Second edition by Littell et al. (2006).
Our aim in this section is to give a basic description of the most useful PROC MIXED statements and options to enable those not wishing to learn the procedure in depth to perform mixed models analyses. Details on the many other options available can be found in the SAS documentation. The presentation in this section will assume a working knowledge of SAS.
Syntax
The statements available in PROC MIXED in version 9.3 are as follows: PROC MIXED statement, BY, CLASS, CONTRAST, ESTIMATE, ID, LSMEANS, LSMESTIMATE, MODEL, PARMS, PRIOR, RANDOM, REPEATED, SLICE, STORE, and WEIGHT statements. In addition, ODS statements can be used to control what is printed when running PROC MIXED and what is output in SAS datasets for handling by other procedures. The BY statement is the same as in other SAS procedures and will not be considered further in this chapter. We will mention all of the other statements, at least briefly, while concentrating on those statements we have used in this book. Those with older versions of SAS may find that some of the statements listed here are not implemented in their version.
Simple example
Data from the multi-centre hypertension trial introduced in Section 1.3 will be used to illustrate the use of PROC MIXED to fit a simple random effects model. The following code fits a random effects model with pre-treatment DBP (dbp1) and treatment effects fixed and centre and centre·treatment effects random.
PROC MIXED; CLASS centre treat;
MODEL dbp = dbp1 treat;
RANDOM centre centre*treat;The Mixed Procedure | ||
Model Information | ||
Data Set | WORK.A | |
Dependent Variable | dbp | |
Covariance Structure | Variance Components | |
Estimation Method | REML | |
Residual Variance Method | Profile | |
Fixed Effects SE Method | Model-Based | |
Degrees of Freedom Method | Containment | |
Class Level Information | ||
Class | Levels | Values |
centre | 29 | 1 2 3 4 5 6 7 8 9 11 12 13 14 |
15 18 23 24 25 26 27 29 30 31 | ||
32 35 36 37 40 41 | ||
treat | 3 | A B C |
Dimensions | ||
Covariance Parameters | 3 | |
Columns in X | 5 | |
Columns in Z | 108 | |
Subjects | 1 | |
Max Obs Per Subject | 288 | |
Number of Observations | ||
Number of Observations Read | 288 | |
Number of Observations Used | 288 | |
Number of Observations Not Used | 0 | |
Iteration History | |||
Iteration | Evaluations | −2 Res Log Like | Criterion |
0 | 1 | 2072.30225900 | |
1 | 3 | 2055.64188178 | 0.00000322 |
2 | 1 | 2055.63936685 | 0.00000000 |
Convergence criteria met. | |||
The Model Information gives basic information on the dataset that was used and some methodological information on how the model was fitted (in this case using the default options). The Class Level Information provides us with the values in our dataset for those categorical variables specified in the CLASS statement. Dimensions show the size of the matrices that SAS is working with. It is potentially confusing that the number of subjects is shown as one when we have 288 patients in the trial. This is because our dataset has not been ‘blocked’ (see Section 6.2). The Number of Observations allows us to see if any observations have been excluded from analysis, perhaps, because of missing values. The Iteration History table shows how quickly the algorithm has converged. The criterion is a measure of convergence and should be very close to zero. In this example, convergence has been reached quickly. The table gives the value of minus twice the REML log likelihood. If this is very large, then it is likely that the covariance matrix, V, is singular, leading to an infinite likelihood. In this situation, the results would be invalid and the model would need to be respecified, probably refitting certain random effects as fixed or removing them altogether. The Evaluations column gives the number of evaluations of the objective function carried out at each iteration. Occasionally, a message stating that the G matrix is not positive definite will appear. Usually, this indicates that a negative variance component has been set to zero by PROC MIXED and is not a cause for concern. However, if this is not the case, it is possible that only a local maximum has been reached and a ‘grid search’ for other solutions might be advisable (see the PARMS statement).
Covariance Parameter | |
Estimates | |
Cov Parm | Estimate |
centre | 6.4628 |
centre*treat | 4.0962 |
Residual | 68.3677 |
This gives the variance parameter estimates. The variance component for centres is 6.46 and for the centre·treatment interaction 4.10. The residual estimate is 68.37.
Fit Statistics | |
−2 Res Log Likelihood | 2055.6 |
AIC (smaller is better) | 2061.6 |
AICC (smaller is better) | 2061.7 |
BIC (smaller is better) | 2065.7 |
This table gives information about the model fit. It includes several statistics based on the likelihood value. AIC is Akaike’s Information Criterion, AICC is a variation on AIC and BIC is Schwartz’s Bayesian Information Criterion. Each of these criteria attempts to make adjustment for the number of parameters fitted in the model so that models can be compared directly. However, note that SAS presents minus twice the usual criteria. They are of greatest value for comparing models using different covariance patterns (see Chapter 6). More detail on their calculation is given in the SAS documentation.
Type 3 Tests of Fixed Effects | ||||
Num | Den | |||
Effect | DF | DF | F Value | Pr > F |
dbp1 | 1 | 208 | 6.31 | 0.0128 |
treat | 2 | 48 | 2.28 | 0.1131 |
Results from F tests are given for all fixed effects. The ‘Type 3’ tests are the Wald tests described in Section 2.4.4. These tests arise naturally from mixed models and adjust for other effects fitted in the model. The denominator DF for the F tests are given by the residual DF or, if the fixed effect is contained, by the DF of the containing effect. Here dbp1 is tested using the residual DF of 208 and treat using the centre·treatment DF of 48, since it is contained within this effect. Other methods for calculating the denominator DF are available by using the DDFM option in the MODEL statement (see the following section).
We will now give basic details on the use of each statement within the procedure.
The PROC MIXED statement
This statement initiates the procedure, and its options are concerned with the general aspects of fitting the procedure and specifying its output.
PROC MIXED options;Some of the more useful PROC MIXED options are listed in the following table.
METHOD = <method> | Specifies estimation method. |
= REML | REML (default). |
= ML | Maximum likelihood. |
= MINQUE | Minimum variance quadratic variance estimation. This is an estimation method that we have not covered. It is based on equating mean squares to their expected values, and it is less computationally expensive than maximum likelihood. Further information can be found in Rao (1971 1972). Searle et al. (1992) show that the solution is equivalent to that obtained using just one iteration with REML. |
CL | Prints Wald confidence intervals for covariance parameters. Default is 95% limits unless ALPHA=<p> option is used. |
ASYCOV | Prints asymptotic covariance matrix of covariance parameters. |
EMPIRICAL | Empirical estimator of variance matrix of fixed effects, 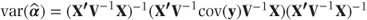 , is used in place of V for all fixed effects variance estimates in covariance pattern models fitted using , is used in place of V for all fixed effects variance estimates in covariance pattern models fitted using REPEATED statement (see Section 2.4.3). |
IC | Displays additional information criteria to compare model fit. Criteria due to Akaike–AIC and AICC (1974), Hannan and Quinn–HQIC (1979), Schwarz–BIC (1978) and Bozdogan–CAIC (1987) are displayed. |
NOCLPRINT | Suppresses printing of class levels. (This is useful when a CLASS effect has many categories.) |
NOINFO | Suppresses printing of Model Information, Dimensions and Number of Observations tables. |
NOITPRINT | Suppresses printing of Iteration History |
PLOTS options | A variety of statistical graphics can be specified via the Output Delivery System (in more recent versions of SAS). See online help for details |
The MODEL statement
This statement is used to specify the dependent variable and the fixed effects in the model. Options are available for specifying the model, significance tests and for requesting specific output to be printed.
MODEL <dependent> = <fixed effects>/options;Options relating to the model specification
NOINT | Requests no intercept be included in the model. |
Options relating to statistical tests
DDFM =<DF type> | Selects DF type for F test denominator DF for all F tests. |
RESIDUAL | Uses residual DF. |
CONTAIN | If the effect of interest is contained within another effect, then the DF of the containing effect are used. If the effect is not contained, then the residual DF are used. These are the default DF. |
BETWITHIN | Assigns between- or within-subject DF to effects when the REPEATED statement is used. Effects nested within the SUBJECT effect take the subject effect DF, others take the residual DF. |
SATTERTH | Uses Satterthwaite’s approximation to the true DF (see Section 2.4.4). |
KR <(FIRSTORDER)> or KENWARDROGER <(FIRSTORDER)> | Calculates DF suggested by Kenward and Roger (1997). This substitutes an improved estimate of the covariance matrix of the fixed and random effects into Satterthwaite’s approximation for the DF (see Section 2.4.3). It also causes the improved estimates of fixed and random effects variances to be used throughout the whole procedure (e.g. for calculating standard errors and test statistics). Addition of the FIRSTORDER or LINEAR sub-option will sometimes lead to an improved adjustment in certain types of covariance pattern model (see Section 6.2.4). |
Options relating to output
SOLUTION | Solution for fixed effects is printed. |
CL | Requests t-type confidence intervals for fixed effects given by SOLUTION option. |
ALPHA=<p> | Specifies size of confidence intervals (default 0.05). |
E3 | Prints design matrix for all fixed effects. |
OUTP=<dataset> | For each observation gives predicted values 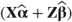 and residuals and residuals 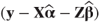 based on fixed and random effects. Approximate variances, standard errors and 95% confidence intervals for each predicted value are also listed. based on fixed and random effects. Approximate variances, standard errors and 95% confidence intervals for each predicted value are also listed. |
OUTPM=<dataset> | Predicted values 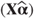 and residuals and residuals 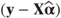 based on fixed effects only are given. Approximate variances, standard errors and 95% confidence intervals for each predicted value are also listed. based on fixed effects only are given. Approximate variances, standard errors and 95% confidence intervals for each predicted value are also listed. |
Options relating to model checking
RESIDUAL | Produces residual plots when used with ODS graphics. |
INFLUENCE | Influence diagnostic plots to be produced when used with ODS graphics. |
VCIRY | Standardises the residuals in a covariance pattern model |
| (see Section 6.2.4). |
Example
PROC MIXED DATA=a; CLASS centre treat;
MODEL dbp = dbp1 treat/ E3 SOLUTION DDFM=KR OUTP=pred
OUTPM=predm;
RANDOM centre centre*treat;
PROC PRINT NOOBS DATA=pred;
PROC PRINT NOOBS DATA=predm;
Use of the SOLUTION and DDFM=KR options
Solution for Fixed Effects | ||||||
Standard | ||||||
Effect | treat | Estimate | Error | DF | t Value | Pr > |t| |
Intercept | 61.7638 | 11.2440 | 284 | 5.49 | <.0001 | |
dbp1 | 0.2689 | 0.1084 | 284 | 2.48 | 0.0137 | |
treat | A | 2.9274 | 1.4109 | 25.6 | 2.07 | 0.0482 |
treat | B | 1.6415 | 1.4453 | 25.7 | 1.14 | 0.2666 |
treat | C | 0 | ·· | ·· | ·· | ·· |
Note that use of DDFM=KR has caused the standard errors to be based on an improved estimate (as described by Kenward and Roger, 1997), which helps alleviate bias (see Section 2.4.3). These standard errors are also used to calculate the t statistics and their approximate DF. (It is somewhat confusing that the DDFM=KR option in fact relates to the standard error calculation. The DF are still calculated using Satterthwaite’s approximation but based on these improved standard errors.)
Use of the E3 option
Type 3 Coefficients for dbp1 | ||
Effect | treat | Row1 |
Intercept | ||
dbp1 | 1 | |
treat | A | |
treat | B | |
treat | C |
Type 3 Coefficients for treat | |||
Effect | treat | Row1 | Row2 |
Intercept | |||
dbp1 | |||
treat | A | 1 | |
treat | B | 1 | |
treat | C | −1 | −1 |
This shows that SAS has parameterised treatment effects by using differences from the last treatment (C).
Use of the DDFM=KR option
Type 3 Tests of Fixed Effects | ||||
Num | Den | |||
Effect | DF | DF | F Value | Pr > F |
dbp1 | 1 | 284 | 6.16 | 0.0137 |
treat | 2 | 25 | 2.16 | 0.1364 |
Note that these tests differ from the earlier analysis where the DDFM=KR option was not used.
Use of the OUTP= option
S | ||||||||||||||
t | ||||||||||||||
d | ||||||||||||||
p | E | |||||||||||||
a | c | r | ||||||||||||
t | v | e | t | r | A | L | U | R | ||||||
i | i | n | r | d | P | P | l | o | p | e | ||||
e | s | t | e | d | b | c | r | r | p | w | p | s | ||
n | i | r | a | b | p | c | f | e | e | D | h | e | e | i |
t | t | e | t | p | 1 | f | 1 | d | d | F | a | r | r | d |
1 | 6 | 29 | C | 86 | 97 | . | 1 | 84.9727 | 3.16871 | 18.4533 | 0.05 | 78.3272 | 91.618 | 1.0273 |
2 | 3 | 29 | C | 72 | 109 | . | . | 88.1995 | 3.15570 | 17.9756 | 0.05 | 81.5690 | 94.830 | −16.1995 |
3 | 6 | 5 | B | 109 | 117 | . | 5 | 96.4061 | 3.03187 | 47.2421 | 0.05 | 90.3076 | 102.505 | 12.5939 |
4 | 6 | 5 | A | 87 | 100 | 3 | 1 | 93.7690 | 2.78800 | 16.4832 | 0.05 | 87.8727 | 99.665 | −6.7690 |
5 | 6 | 29 | A | 85 | 105 | 3 | 3 | 90.6234 | 3.25199 | 11.7170 | 0.05 | 83.5189 | 97.728 | −5.6234 |
7 | 6 | 3 | A | 100 | 114 | 1 | 2 | 99.9119 | 3.01901 | 20.6093 | 0.05 | 93.6263 | 106.198 | 0.0881 |
8 | 6 | |||||||||||||
etc. | ||||||||||||||
Use of the OUTPM= option
S | ||||||||||||||
t | ||||||||||||||
d | ||||||||||||||
p | E | |||||||||||||
a | c | r | ||||||||||||
t | v | e | t | r | A | L | U | R | ||||||
i | i | n | r | d | P | p | l | o | p | e | ||||
e | s | t | e | d | b | c | r | r | p | w | p | s | ||
n | i | r | a | b | p | c | f | e | e | D | h | e | e | i |
t | t | e | t | p | 1 | f | 1 | d | d | F | a | r | r | d |
1 | 6 | 29 | C | 86 | 97 | . | 1 | 87.8475 | 1.31873 | 95.212 | 0.05 | 85.2296 | 90.4655 | −1.8475 |
2 | 3 | 29 | C | 72 | 109 | . | . | 91.0744 | 1.29205 | 85.384 | 0.05 | 88.5056 | 93.6432 | −19.0744 |
3 | 6 | 5 | B | 109 | 117 | . | 5 | 94.8671 | 1.95897 | 189.699 | 0.05 | 91.0029 | 98.7313 | 14.1329 |
4 | 6 | 5 | A | 87 | 100 | 3 | 1 | 91.5816 | 1.17842 | 58.874 | 0.05 | 89.2235 | 93.9397 | −4.5816 |
5 | 6 | 29 | A | 85 | 105 | 3 | 3 | 92.9262 | 1.13687 | 55.620 | 0.05 | 90.6484 | 95.2039 | −7.9262 |
7 | 6 | 3 | A | 100 | 114 | 1 | 2 | 95.3463 | 1.61199 | 153.490 | 0.05 | 92.1617 | 98.5309 | 4.6537 |
etc. | ||||||||||||||
Options relating to model checking
Use of these options is illustrated in Section 2.5 and Section 6.3.
The RANDOM statement
This statement can be used to specify random effects and/or random coefficients, β, and the form of their variance matrix, G. Several RANDOM statements may be specified, although usually only one will be needed. When no RANDOM statement is included, the results will be the same as those obtained using PROC GLM.
RANDOM <random effects>/options;Output options
CL | Requests t-type confidence intervals for each random effects estimate. |
ALPHA=<p> | Specifies size of confidence interval (default is 0.05 to give 95% confidence intervals). |
SOLUTION | Solution for random effects is printed. |
Options corresponding to the G and V matrices
G | Prints G. |
GCORR | Prints correlation matrix corresponding to G. |
V | Prints V. |
VCORR | Prints correlation matrix corresponding to V. |
GDATA=<dataset> | Specifies a fixed G matrix. |
Example
PROC MIXED DATA=a; CLASS centre treat;
MODEL dbp = dbp1 treat/ DDFM=KR;
RANDOM centre centre*treat/ V SOLUTION;Use of the V option
| Estimated V Matrix for Subject 1 | |||||||
| Row | Col1 | Col2 | Col3 | Col4 | Col5 | Col6 | Col7 |
| 1 | 78.9267 | 10.5590 | 6.4628 | ||||
| 2 | 10.5590 | 78.9267 | 6.4628 | ||||
| 3 | 78.9267 | 6.4628 | |||||
| 4 | 6.4628 | 78.9267 | |||||
| 5 | 6.4628 | 6.4628 | 78.9267 | ||||
| 6 | 78.9267 | 6.4628 | |||||
This matrix has a dimension equal to the number of observations in the dataset and is hence very large in this example. (If a SUBJECT option is used in the RANDOM statement, the matrix will relate to only the first subject, otherwise the full variance matrix for all observations is given.) The diagonal terms are equal to the sum of the three variance components. Off-diagonal terms are equal to the sum of the centre and centre·treatment variance components, 10.6, when patients are at the same centre and receive the same treatment; they are equal to the centre variance component, 6.5, when patients are at the same centre but receive different treatments; they and are zero when patients are at different centres (denoted by blank entries).
Use of the SOLUTION option
Solution for Random Effects | |||||||
Std Err | |||||||
Effect | treat | centre | Estimate | Pred | DF | t Value | Pr > |t| |
centre | 1 | 0.7966 | 1.8325 | 20.7 | 0.43 | 0.6683 | |
centre | 2 | −2.3441 | 2.1884 | 14.5 | −1.07 | 0.3016 | |
centre | 3 | 1.9760 | 2.2547 | 12.1 | 0.88 | 0.3978 | |
centre | 4 | −0.1429 | 2.1410 | 16.4 | −0.07 | 0.9476 | |
centre | 5 | 1.1779 | 2.1764 | 15.4 | 0.54 | 0.5961 | |
| · | |||||||
| · | |||||||
centre | 31 | −4.7913 | 1.8470 | 21.5 | −2.59 | 0.0167 | |
| · | |||||||
| · | |||||||
centre*treat | A | 1 | −0.4605 | 2.2025 | 2.36 | −0.21 | 0.8511 |
centre*treat | B | 1 | 1.6900 | 2.1965 | 2.38 | 0.77 | 0.5106 |
centre*treat | C | 1 | −0.7246 | 2.2093 | 2.3 | −0.33 | 0.7705 |
centre*treat | A | 2 | −0.8330 | 2.2406 | 1.56 | −0.37 | 0.7543 |
| · | |||||||
| · | |||||||
| · |
The Estimate and Std Err Pred columns give the random effects estimates and their standard errors. The Wald t tests help to determine whether any centre is outlying.
Options for specifying the G matrix structure
GROUP=<effect> | This causes a separate G matrix to be estimated within each group. For example, if patient effects were fitted as random and the GROUP=treat option were used, then a separate variance patient component would be estimated for each treatment group. If patients 1 and 3 received treatment A and patients 2 and 4 received treatment B, then the G matrix for the first four patients would have the form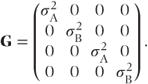 |
However, the statement should be used cautiously when there are many group levels, since a large number of parameters will then need to be estimated.
The G matrix is always diagonal in random effects models, and the following options given for the RANDOM statement are not required. However, a non-diagonal G matrix is necessary to fit a random coefficients model to allow the intercepts and slopes of the random coefficients to be correlated and also for fitting certain covariance structures in hierarchical repeated measures designs (see Section 8.1). The G matrix is blocked by the specified SUBJECT effect, and the covariance pattern is specified by the TYPE options in a very similar way to the REPEATED statement.
RANDOM <random effects or coefficients>/
SUBJECT=<blocking effect> TYPE=<covariance pattern>;Covariance patterns available for the TYPE= option will be listed under the REPEATED statement.
Random coefficients models In these models, the random coefficients on the same subject are assumed to be correlated (e.g. intercepts and slope effects are correlated for each subject in a repeated measures trial). This is achieved using a RANDOM statement of the following form:
RANDOM <random coefficients>/SUBJECT=<subject effect> TYPE=UN;For example, to model random coefficients for the effect of time, the code might be
RANDOM INT time/SUBJECT=patient TYPE=UN;This fits the random coefficients patient and patient·time. Patient effects are specified by the reserved SAS term INT, which fits an intercept for each patient.
Example
Examples of fitting random coefficients models are given in Section 6.6.
The LSMEANS statement
This statement calculates the least squares mean estimates of specified fixed effects.
LSMEANS <fixed effects>/options;Options
CL | Requests t-type confidence intervals for least squares means. |
ALPHA=<p> | Specifies size of confidence interval (default is 0.05 for a 95% confidence interval). |
ADJUST=<type> | Requests adjusted p-values for multiple comparisons (see manual for further details). |
DIFF | Prints differences between each pair of least squares means. |
PDIFF | Prints p-values for comparisons between each pair of least squares means, by default. PDIFF=CONTROL compares difference with a control group (first level of the LSMEANS variables, by default). |
AT<variables>= <values> | Modifies the covariate value(s) at which LSMEANS are computed. Otherwise they are evaluated at mean values. |
Example
PROC MIXED; CLASS centre treat;
MODEL dbp = dbp1 treat/ DDFM=KR;
RANDOM centre centre*treat;
LSMEANS treat/ CL COV CORR DIFF PDIFF;Least Squares Means | |||||||||
Standard | |||||||||
Effect | treat | Estimate | Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper |
treat | A | 92.3491 | 1.1233 | 52 | 82.21 | <.0001 | 0.05 | 90.0951 | 94.6032 |
treat | B | 91.0632 | 1.1695 | 51.4 | 77.86 | <.0001 | 0.05 | 88.7157 | 93.4107 |
treat | C | 89.4217 | 1.1326 | 58.7 | 78.96 | <.0001 | 0.05 | 87.1552 | 91.6882 |
Least Squares Means | |||||||||
Effect | treat | Cov1 | Cov2 | Cov3 | Corr1 | Corr2 | Corr3 | ||
treat | A | 1.2619 | 0.2923 | 0.2770 | 1.0000 | 0.2225 | 0.2177 | ||
treat | B | 0.2923 | 1.3678 | 0.2807 | 0.2225 | 1.0000 | 0.2119 | ||
treat | C | 0.2770 | 0.2807 | 1.2827 | 0.2177 | 0.2119 | 1.0000 | ||
The last six columns show covariance and correlation matrices for the least squares means.
Differences of Least Squares Means | ||||||||
Standard | ||||||||
Effect | treat | −treat | Estimate | Error | DF | t Value | Pr > |t| | Alpha |
treat | A | B | 1.2859 | 1.4300 | 23.8 | 0.90 | 0.3775 | 0.05 |
treat | A | C | 2.9274 | 1.4109 | 25.6 | 2.07 | 0.0482 | 0.05 |
treat | B | C | 1.6415 | 1.4453 | 25.7 | 1.14 | 0.2666 | 0.05 |
Differences of Least Squares Means | ||||
Effect | treat | −treat | Lower | Upper |
treat | A | B | −1.6665 | 4.2384 |
treat | A | C | 0.02511 | 5.8297 |
treat | B | C | −1.3314 | 4.6144 |
Note that the DF differ markedly between the least squares means and their differences because they are estimated using information from different combinations of error strata.
The ESTIMATE statement
This statement calculates a linear function of fixed and/or random effects estimates (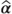 and
and 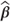 ).
).
ESTIMATE ‘<label>’ <fixed effect1> <values>
<fixed effect2><values>
… |
<random effect 1> <values>
<random effect 2> <values>
… / options;Options
CL | Requests t-type confidence intervals for estimate. |
ALPHA=<p> | Specifies size of confidence interval (default is 0.05 for a 95% CI). |
DIVISOR=<n> | Value by which to divide all coefficients so that fractional coefficients can be entered as integer numerators. |
E | Shows the effect coefficients used in the estimate (useful to check ordering if interaction effects are used). |
When the effect of interest is contained within another fixed interaction effect, the coefficients for this effect are automatically included in the estimate by SAS. For example, the following code for a fixed effects analysis of the multi-centre hypertension data
PROC MIXED; CLASS centre treat;
MODEL dbp = dbp1 treat centre centre*treat/ DDFM=KR;
ESTIMATE ‘A−B’ treat 1 −1 0/ E CL;would cause the following coefficients to be used by SAS for constructing the estimate.
Coefficients for A-B | |||
Effect | treat | centre | Row1 |
centre | 4 | ||
centre | 5 | ||
centre | 6 | ||
centre | 7 | ||
centre | 8 | ||
centre | 9 | ||
centre | 11 | ||
. | |||
. | |||
. | |||
centre*treat | A | 1 | 0.0385 |
centre*treat | B | 1 | -0.04 |
centre*treat | C | 1 | |
centre*treat | A | 2 | 0.0385 |
centre*treat | B | 2 | -0.04 |
centre*treat | C | 2 | |
centre*treat | A | 3 | 0.0385 |
. | |||
. | |||
. |
The centre·treatment coefficients are equal to 1/ni, where ni is the number of centres at which treatment i is received (26 for treatment A and 25 for treatment B). Because treatments A and B are not received at every centre, this estimate is in fact ‘non-estimable’, and SAS gives the following output:
Estimates | ||||||||
Standard | ||||||||
Label | Estimate | Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper |
A-B | Non-est | . | . | . | . | . | . | . |
However, if the containing effect is fitted as random, SAS does not include any coefficients for this containing effect in the estimate. For example, the following code for a random effects analysis of the multi-centre hypertension data
PROC MIXED; CLASS centre treat;
MODEL dbp = dbp1 treat/DDFM=KR;
RANDOM centre centre*treat;
ESTIMATE ‘A−B’ treat 1 −1 0/ E CL;would cause the following coefficients to be used by SAS for constructing the estimate:
Coefficients for A-B | ||
Effect | treat | Row1 |
Intercept | ||
dbp1 | ||
treat | A | 1 |
treat | B | -1 |
treat | C | |
Estimates | ||||||||
Standard | ||||||||
Label | Estimate | Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper |
A-B | 1.2859 | 1.4300 | 23.8 | 0.90 | 0.3775 | 0.05 | -1.6665 | 4.2384 |
The ESTIMATE statement can also be used to estimate shrunken random effects by specifying the coefficients of the random effects. For example, to estimate the shrunken difference between the first two treatments within the first two centres, the following ESTIMATE statements can be added to the previous code:
ESTIMATE ‘C1, A−B’ treat 1 −1 0| centre*treat 1 − 1 0/ E CL;
ESTIMATE ‘C2, A−B’ treat 1 −1 0| centre*treat
0 0 0 1 − 1 0/ CL;These cause the following coefficients to be used for the first estimate
Coefficients for C1, A-B | |||
Effect | treat | centre | Row1 |
Intercept | |||
dbp1 | |||
treat | A | 1 | |
treat | B | -1 | |
treat | C | ||
centre | 1 | ||
centre | 2 | ||
centre | 3 | ||
. | |||
. | |||
. | |||
centre | 41 | ||
centre*treat | A | 1 | 1 |
centre*treat | B | 1 | -1 |
centre*treat | C | 1 | |
centre*treat | A | 2 | |
centre*treat | B | 2 | |
centre*treat | C | 2 | |
centre*treat | A | 3 | |
. | |||
. | |||
. | |||
centre*treat | A | 41 | |
centre*treat | B | 41 | |
centre*treat | C | 41 |
and give the following estimates:
Estimates | ||||||||
Standard | ||||||||
Label | Estimate | Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper |
C1, A-B | -0.8646 | 2.8933 | 7.35 | -0.30 | 0.7733 | 0.05 | -7.6405 | 5.9113 |
C2, A-B | 1.6405 | 3.4054 | 2.65 | 0.48 | 0.6669 | 0.05 | -10.0418 | 13.3229 |
The CONTRAST statement
This statement can be used to define F tests for fixed and random effects. A single or multiple contrast, C, can be defined by
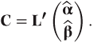
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


