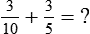Review of Basic Mathematical Skills

Chapter 2


Review of Basic Mathematical Skills



Objectives



• Add, subtract, multiply, and divide whole numbers


• Add, subtract, multiply, and divide fractions and reduce fractions to the lowest terms


• Add, subtract, multiply, and divide mixed numbers and reduce to the lowest terms


• Add, subtract, multiply, and divide decimals and round them to a specific number place value


• Convert fractions to decimal fractions


• Convert among fractions, decimals, and percentages


• Express numbers in ratio and proportion and solve for unknowns



Key Words





























Pretest


Complete the following answers, and show all of your work. Round all decimals to the closest thousandth unless otherwise stated.



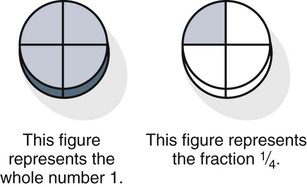
1. image = __________


2. 154 + 1063 + 25 + 2376 = __________


3. 163 − 69 = __________


4. 256 × 42 = __________


5. 256 ÷ 16 = __________


6. 3655 − 29 = __________


7. 25.6 + 1456 + 35.67 = __________


8. 354.29 − 45.390 = __________


9. 12.56 × 65.031 = __________


10. 655.08 ÷ 1.2 = __________


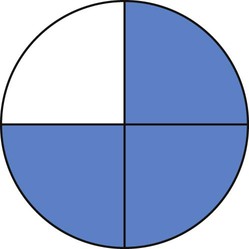
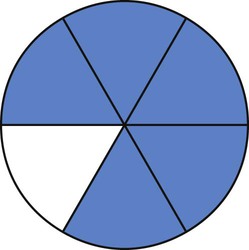
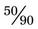11. image = __________


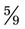12. image = __________


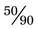13. image = __________


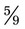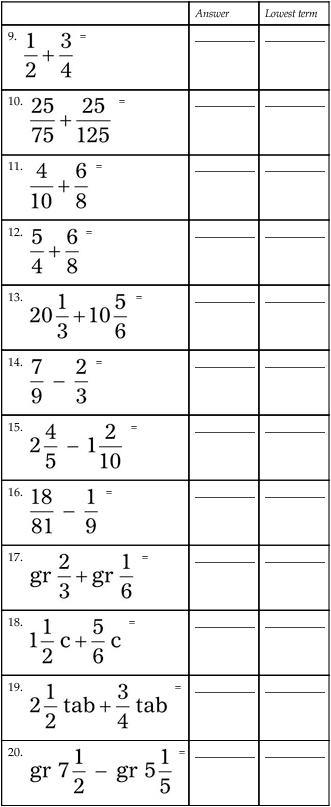
14. image = __________


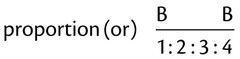
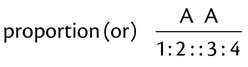
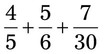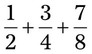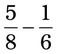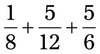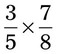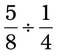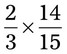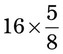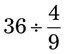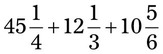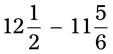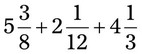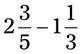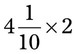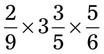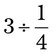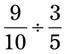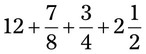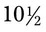15. image = __________


16. image = __________


17. image = __________


18. image = __________


19. image = __________


20. image = __________


21. image = __________


22. image = __________


23. image = __________


24. image = __________


25. image = __________


26. image = __________


27. image = __________


28. 100.2 × 100.03 = __________


29. 721 − 0.01 = __________


30. 12.02 ÷ 6.01 = __________


31. A roll of adhesive is image inches long. The physician asks you to be sure the person has sufficient amount to apply bandages daily for 2 weeks using approximately 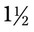image yards per bandage. How many rolls of adhesive should you be sure the patient buys?


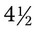32. A solution contains image cups of water. How many milliliters would be in 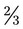image of the solution?


    Round the following to the nearest one hundredth.


33. 75.0023 __________


34. 12.015 __________


35. 6.12453 __________


36. 126.444 __________


    Change the following to decimal fractions.


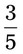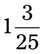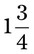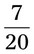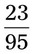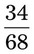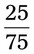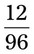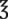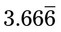37. image __________


38. image __________


39. image __________


40. image __________


    Change the following to ratios and reduce to the lowest terms possible.


41. image __________


42. image __________


43. image __________


44. image __________


    Solve the following proportions.


45. x : 3 :: 15 : 30 = __________


46. 5 : 15 :: 8 : x = __________


47. 3 : x :: 11 : 33 = __________


48. 1 : 50 :: x : 40 = __________


49. A pharmacist is able to fill six prescriptions in 10 minutes with the assistance of a pharmacy tech. How many prescriptions can be completed in 1 hour?


50. A prescription calls for 15 mL of water to reconstitute a medication in a 20-mL vial. How many milliliters of water would be needed proportionally to reconstitute 50-mL vial of the same medication?


    Interpret the following abbreviations.


51. mL __________


52. tsp __________


53. mg __________


54. g __________


55. gr __________


56. mcg __________


57. tbsp __________


58. image __________


59. image __________


60. pt __________





Whole Numbers


What Is a Whole Number?


A whole number is the basic mathematical symbol that we use on a daily basis. In the math world, whole numbers represent numerals consisting of one or more digits. The digits used in math are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Numbers may also be written in words, such as one, two, ten, one thousand, ten million one hundred three, and the like. The word “and” should not be used between digits in a whole number. In the medical field, commas are not placed in numbers with more than four digits or seven digits, such as 1275 or 2356302. A comma might be misinterpreted as a decimal when used in whole numbers, causing a medication error.


A whole number does not have a decimal, fraction, or percentage. When you add, subtract, or multiply whole numbers, the answer will always remain a whole number such as 10, 25, or 100. For example, 45 + 12 = 57 or 5 × 45 = 225 because all of the numbers are whole numbers. In some cases if dividing whole numbers, the answer may be found as a whole number, a decimal number, or a whole number with a decimal number. For example, 10 divided by 2 is 5 or 11 divided by 3 would be image; all the numbers in this example contain whole numbers, but they are not evenly divisible and may have decimal remainders.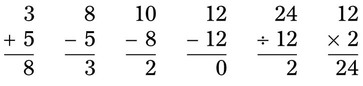



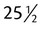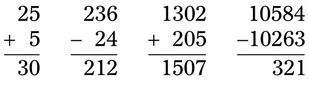
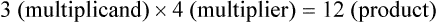
Example 2-1


image




A whole number is always to the left of a decimal point. The numeral 0 is a whole number with the decimal understood to be at the right side of the zero. In pharmaceutical mathematics, if no number is to the left of a decimal, a zero (0) is placed in the whole number place.



Tech Note


Whole numbers are numbers found to the left of the decimal point and may have one digit or more. Fractions and decimals may be added to a whole number, but the whole number is to the left in each of these cases. Examples: 25, 25.1, image.



Tech Note


Whole numbers are used in strengths of medications, doses of medications, inventory, and costs of medications, to give just a few examples of the need to understand this concept.



Adding and Subtracting Whole Numbers


When adding or subtracting whole numbers, align the digits from the right and then add or subtract one set of digits at a time starting from the right (from ones to tens to hundreds, etc.). Addition is finding a sum or total of two numbers. Subtraction is finding the difference between two numbers.



Example 2-2


image



Practice Problems A


Calculate the following problems, being sure to show your work and stating measurement designations as appropriate.



1. 25 + 56 = __________


2. 105 + 235 = __________


3. 1243 + 356 = __________


4. 50 g + 100 g = __________


5. 25 mg + 90 mg = __________


6. 240# + 133# = __________


7. 125,000 units + 250,000 units = __________


8. 7500 mL + 1000 mL = __________


9. 78 − 56 = __________


10. 285 − 168 = __________


11. 1549 − 1374 = __________


12. 725 mL − 650 mL = __________


13. 525 g − 175 g = __________


14. 156# − 48# = __________


15. 65 mL − 30 mL = __________


16. 350 mg − 125 mg = __________


17. 1250 mg − 615 mg = __________


18. 266 kg − 15 kg = __________


19. A bottle of antibiotic needs to be reconstituted with 100 mL of distilled water. You have a calibrated graduate that holds 50 mL. How many times will you have to fill the container with water to reconstitute the medication? __________


20. A vial of anesthetic contains 10 mL. The pharmacist asks that you add 30 mL of distilled water to prepare an anesthetic compound for mouth ulcers. How many milliliters will be in the bottle of prepared medication? __________



Multiplying Whole Numbers


Multiplication of whole numbers is actually a shortcut to repeated addition of numbers. When multiplying whole numbers, align the numbers or factors as you would for addition or subtraction. The use of “×” denotes that the numbers should be multiplied to find a product. Either number may be the multiplier or multiplicand and the product will not be affected. However, it requires less calculating if the multiplier has the fewer digits. You should also remember that if a number is multiplied by zero, the product is zero. First multiply the number in the multiplicand (number that is to be multiplied or is multiplied by another or the number on top of the problem) by the number at the far right of the multiplier (number that is used to multiply another number or that on the bottom of the equation).



Example 2-3


3 (multiplicand)×4 (multiplier)=12 (product)


image


Multiply the remaining numbers in the subsequent digits, moving from right to left. Be sure to keep the numbers to the far right in alignment with the numbers in the multiplier. Finally, add the numbers that have been multiplied to obtain the product.



Example 2-4


image



Example 2-5


image


Please notice the zero or “0”s are now in the first product line and then multiply the numbers following the zero or “0” in the multiplicand in the usual manner. Be sure to keep the alignment correct.



image Tech Alert


If the multiplier is divisible by ten (or ends in “0”) align the multiplier so the “0” is to the right of the multiplicand to shorten the computation of the problem. The number of “0s” to right of first number above zero in the multiplier will then be found to the right of the first line of numbers multiplied.



Dividing Whole Numbers


Division is a way of determining how many times one number can be found in another. It is actually repeated subtraction steps. Division is represented by either “÷” or “image.” The number being divided is called the dividend, and the number used to divide is the divisor. The result of the division is the quotient.



Example 2-6


35 (Dividend)÷5 (Divisor)=7 (Quotient) 


image


OR


image

Any number that is remaining when numbers are not exactly divisible is called a remainder. In math, when rounding numbers, any amount in the remainder (the number that remains after subtraction) that is less than half of the divisor is usually discarded and the number in the quotient remains the same. Conversely, when rounding, if the remainder is more than one half of the divisor, the number in the quotient is increased by one number. For example, 30 divided by 9 is 3, with 3 as a remainder. In this instance, the quotient would remain at 3. But if 33 is divided by 9, the quotient is 3 with a remainder of 6. Six is more than half of 9, so the quotient will become 4.



Learning Tip


Remember that any number divided by itself equals 1 and any number divided by 1 equals that same number. Zero divided by any number remains 0. (Zero can never be the divisor; i.e., 9 ÷ 0 has no meaning, and the answer remains 9.)


When dividing whole numbers, the number in the divisor must be smaller than the number in the dividend to be able to do the calculation. When the divisor is a single digit, the first number of the dividend must be divisible by the divisor or the second digit in the dividend is also used.



Example 2-7


360÷9


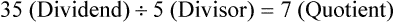
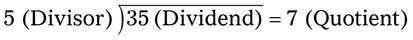
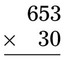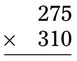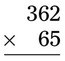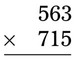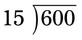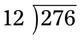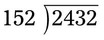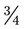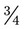image


In this example, 3 cannot be divided by 9, so you must move to 36 to be able to use the divisor 9. Nine will divide into 36 four times, and 9 will divide into 0 zero times, so 360 ÷ 9 = 40.


When there are multiple digits in the divisor, the divisor is rounded to the nearest 10 to estimate the quotient digit. The entire divisor is then used to complete the calculation.



Example 2-8


275÷25


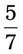
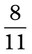
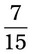
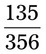
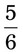
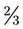image


Estimate to the nearest 10 digit or go from 25 to 30. If you divide 275 by 30, the answer is 9 (3 into 27), but when you multiply 25 by 9, the answer is 225 with 50 as a remainder. If you divide by 10, the answer still has a remainder of 25. So then try 11, and the answer is correct. 11 × 25 = 275 or 275 ÷ 25 = 11.



Learning Tip


When dividing by two, three, or more digit numbers, estimate the numbers before doing the calculation. This will cut down on the errors by helping to discover whether the calculated answers are near to the exact number needed after calculation. Round to the nearest multiple ending in zero. For example, in Example 2-8, the estimation of the divisor would become 25 to show that the quotient should first be close to 10. Thus, your answer of 11 is basically correct.



Practice Problems B


Calculate the following problems, being sure to show all your work. Estimate your work first. Round to the nearest hundreth as appropriate.



1. 56 × 10 = __________


2. 76 × 11 = __________


3. 100 × 87 = __________


4. 768 × 2 = __________


5. 3500 × 265 = __________


6. 345 × 70 = __________


7. image = __________


8. image = __________


9. image =


10. image =


11. 105 ÷ 5 = __________


12. 840 ÷ 40 = __________


13. 296 ÷ 4 = __________


14. 1125 ÷ 15 = __________


15. 150 ÷ 15 = __________


16. 162 ÷ 18 = __________


17. image = __________


18. image = __________


19. image = __________


20. 25 mg × 40 mg = __________


21. 275 mL × 4 mL = __________


22. 24# × 16# = __________


23. 150 mg × 15 mg = __________


24. 30 kg × 400 kg = __________


25. 21 qt × 28 qt = __________


26. 1250 mg ÷ 125 mg = __________


27. 250,000 units ÷ 150 units = __________


28. 2400 kg ÷ 48 kg = __________


29. 300 mg ÷ 15 mg = __________


30. You are asked to fill a prescription that has 10 tablets containing 250 mg each. What is the total actual ingredient of the medication? __________


31. The physician orders 100 tablets of a medication that is to be taken as 1 tablet four times a day until all the medication has been taken. The physician asks that these medications be placed in separate bottles for each week. How many tablets would you put in each bottle? How many bottles of medication should you have available for the pharmacist to check? __________


32. A prescription costs $15, and the customer gives you $50. How much money should you refund to the person? How many $5 bills would you refund to the patient? __________


33. The manufacturer’s label tells you to add 375 mL of water to a medication for reconstitution. You have a container that will hold 125 mL of water. How many times will you need to fill the container to reconstitute the medication correctly? __________


34. Mrs. Jones comes to the pharmacy and tells you that her child has lost her allergy medication. You look at the prescription and read that the original prescription is for 30 tablets to be taken once daily. Fourteen days have passed since Mrs. Jones filled this medication. After consulting with the pharmacist, you are told to replace the lost medication. How many tablets do you need to give Mrs. Jones so that her child can complete her treatment? __________ How many weeks of medication did the child take? __________


35. You are asked to provide the pharmacist with vials of medication to total 1000 mg. Each vial of medication holds 250 mg. How many vials of medication does the pharmacist need? __________



Fractions


What Is a Fraction?


When a whole number or unit is divided into parts, the parts are called fractions. Fractions are designated as proper and improper. A proper fraction is one in which the numerator is less than the denominator or is part of a whole. An improper fraction is defined as a fraction in which the numerator is equal to or greater than the denominator, a fraction that is equal to or greater than one, or a fraction that can be changed to a whole number or a whole number plus a proper fraction. Complex fractions, found later in the text, are fractional expressions in which the numerator, denominator, or both are expressed as fractions such as image.


Fractions may be expressed in the forma/bsuch as3/4orabsuch as34.


image

The “a” is called the numerator (top number found in a fraction). The “b” is the denominator (bottom number of a fraction). Both numbers must be whole numbers, and the denominator cannot be 0 or the resultant answer becomes 0. The denominator also tells how many times the whole unit has been divided.


image

The circle pictured shows a proper fraction. The shaded area shows the part of a whole. Can you tell the number in the numerator and denominator? If you said image you are correct.


Try with this example:


image

If you said the numerator is 5 and the denominator is 6, you are correct.



Tech Note


Fractions are used in pharmacy in both household and apothecary quantities as well as in business math calculations.



Practice Problems C


In the following examples, please indicate the numerator and the denominator.

























1. image Numerator _____________________ Denominator _____________________
2. image Numerator _____________________ Denominator _____________________
3. image Numerator _____________________ Denominator _____________________
4. image Numerator _____________________ Denominator _____________________
5. image Numerator _____________________ Denominator _____________________


image


A fraction can also be thought of as indicating division—the numerator may be divided by the denominator. So when image is written, the fraction actually means 2 ÷ 3. The following illustrates this in pharmaceutical terms: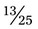


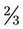If a patient has 25 tablets in a prescription and takes 13 tablets, what is the fractional use?


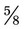Answer: image


A pharmacist has a bottle of medication that contains 90 tablets. He uses 50 tablets. What is the fractional use?


Answer: image or image. (When image is divided by 10 in both the numerator and the denominator, the result is image.)



Tech Note


Whole numbers are actually fractions in which the numerator is an exact multiple of the denominator. When whole numbers are shown in a graph, the entire area of the graph is shaded versus the shading of parts of the entire area in fractions.


image

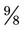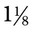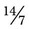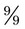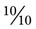A proper or simple fraction is a fraction in which the numerator is less than the denominator, such as image and image. An improper fraction is one in which the numerator is equal to or greater than the denominator, making the fraction a number of one or more such as image or image and image or 2. If the numerator and denominator are the same, the number becomes 1, such as image or image. An improper fraction may be written as a mixed number (a whole number and a fraction) or as an improper fraction (a fraction that has a numerator equal to or greater than the denominator). To change an improper fraction to a mixed number, the numerator is divided by the denominator and any remainder is written over the denominator, such as 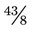image (an improper fraction) = 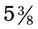image (a mixed number). (When 43 is divided by 8, the answer is 5 with a remainder of 3, so 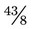image as a mixed number is 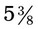image.) The remainder is the amount that is left over after the whole number has been divided into the numerator the maximum number of times (in this problem, 3 is the remainder that now is seen as 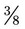image). An improper fraction should always be reduced to a mixed number after calculations have been completed.


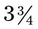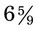A mixed number is a whole number with a proper fraction, such as image and image. To change a mixed number to an improper fraction, multiply the whole number by the denominator and add the amount found in the numerator (e.g., 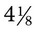image actually means that 4 is multiplied by 8 to provide the whole number of 32 and the 1 found in the numerator of the fraction is added to the total, or 32 + 1 = 33). The denominator remains the number found as the denominator of the mixed number, or 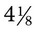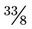image = image. 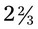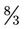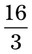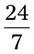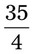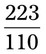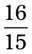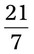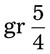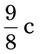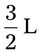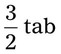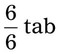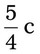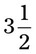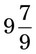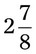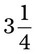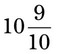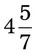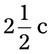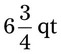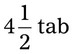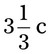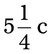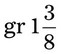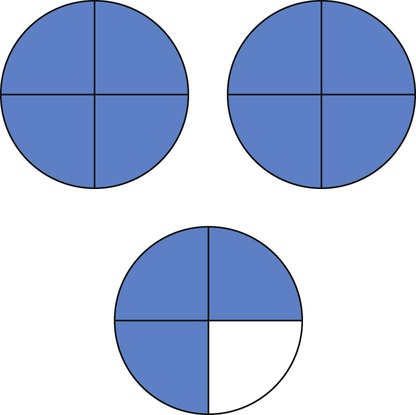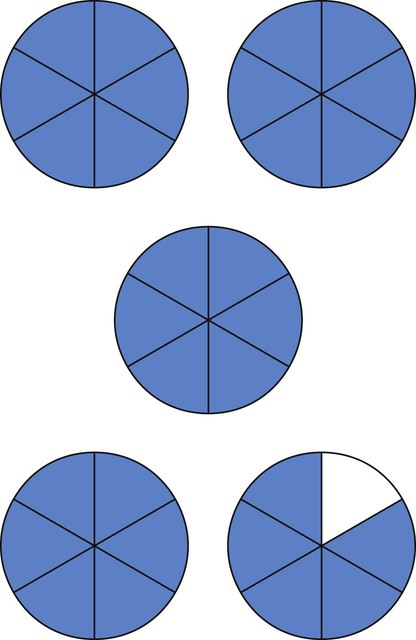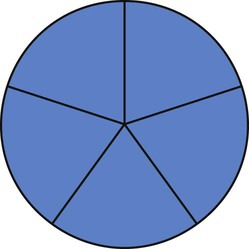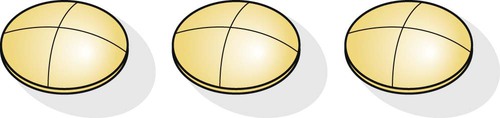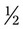Another example of changing a mixed number to an improper fraction is image: 2 × 3 + 2 with the same denominator of 3 or image.



Practice Problems D


Change the following improper fractions to mixed numbers or whole numbers. Show all of your work. Be sure to indicate measurement as appropriate.



1. image = __________


2. image = __________


3. image = __________


4. image = __________


5. image = __________


6. image = __________


7. image = __________


8. image = __________


9. image = __________


10. image = __________


11. image = __________


12. image = __________


    Change the following mixed numbers to improper fractions. Be sure to indicate measurement as appropriate.


13. image = __________


14. image = __________


15. image = __________


16. image = __________


17. image = __________


18. image = __________


19. image = __________


20. image = __________


21. image = __________


22. image = __________


23. image = __________


24. image = __________


    Indicate the fraction or mixed number for each of the following shaded areas.


    image


25. = __________


    image


26. = __________


    image


27. = __________


    image


28. = __________


    image


29. = __________


    image


30. = __________


31. A pharmacist has a medicine cup that is divided into eight equal sections. She fills to the line to indicate five parts. What is the fractional amount that the pharmacist has filled? __________


32. A customer asks you to show him how to divide a tablet (i.e., a scored tablet that is divided into four equal parts) into image of a tablet. Fill in the following tablet to show this fraction.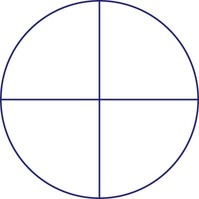


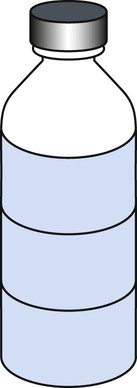
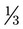image

33. A medication requires that the customer mix granules in image of a glass of water. On the glass, show 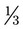image of the glass of water.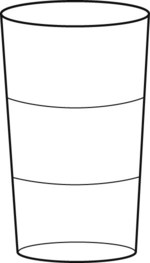


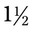image

34. A customer is supposed to take a dose of image tablets four times a day. The prescription drug is in whole tablets. Show what the customer should do.


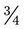image

35. A customer is supposed to give her child image of a medicine dropper of medication. Indicate on the medicine dropper what you would show the customer as a dose.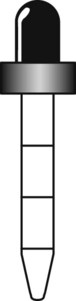


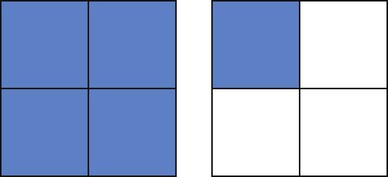
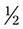image


Reducing Fractions to the Lowest Term


Some fractions, called equivalent fractions, have the same equivalency without having the same portions of a whole. The fraction image could be 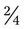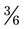image, image, or even 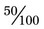image. For example, with 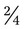image, the numerator and denominator can both be divided by 2 to give 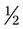image; or with 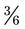image, both parts of the fraction can be divided by 3 for 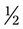image; finally, with 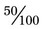image, both components of the fraction can be divided by 50 for 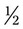image. Each of these fractions is actually one half of the total number of equivalent parts of a whole.



Tech Note


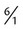Any fraction that has a denominator of 1 is equal to the number in the numerator, such as image = 6.


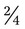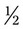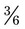Reducing or simplifying fractions to the lowest term is actually the process of finding the lowest equivalent fraction through division of the numerator and denominator by the same number (e.g., the fraction image can be reduced by dividing by 2 [2 ÷ 2 = 1 and 4 ÷ 2 = 2] = image, or image can be reduced by 3 [3 ÷ 3 = 1 and 6 ÷ 3 = 2] to = 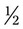image). In each case the reduced fraction contains the same amount of space in each whole. The difference is that the number of divided pieces of the whole has changed. The fractions are comparable, although the actual numerators and denominators have been altered by division with a number that is common to both parts of the fraction. 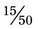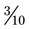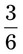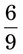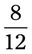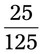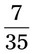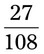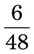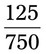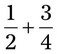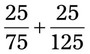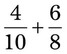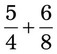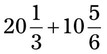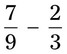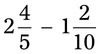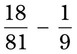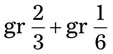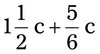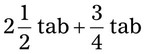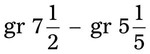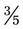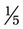This is dividing by a common factor of the numerator and denominator (e.g., with the fraction image, both the numerator and denominator can be divided by 5, so the fraction can be reduced to image).



Learning Tip


Failure to reduce fractions to lowest terms can be cause for the answer to be incorrect because the higher the numbers used, the more difficult the calculations.



Tech Note


If the lowest common denominator is not readily apparent, finding this number may require other steps. One way is to multiply the two denominators together and use that number as the common denominator, or the denominators may be multiplied by 2, 3, or 4 to find a common denominator (e.g., if the denominators are 3 and 4, a common denominator could be 12 because 3 × 4 = 12). If the denominators were 6 and 9, multiplying the 6 by 3 would provide denominator of 18 and multiplying 9 × 2 would also provide the denominator of 18. So in this case the common denominator would be 18, and the math could be calculated using the common denominator.



Practice Problems E


Reduce the following fractions to the lowest term. As always, show your calculations.



Solve the following problems and reduce to the lowest term. Be sure to indicate measurement as appropriate.

























































  Answer Lowest term
9. image = __________ __________
10. image = __________ __________
11. image = __________ __________
12. image = __________ __________
13. image = __________ __________
14. image = __________ __________
15. image = __________ __________
16. image = __________ __________
17. image = __________ __________
18. image = __________ __________
19. image = __________ __________
20. image = __________ __________


image



Adding and Subtracting Fractions


When adding or subtracting fractions, the denominators must be the same numeral. If the denominators are the same number, the numerators may either be added or subtracted (e.g., image + image can be added by adding the numerators, or 3 and 1 [3 + 1] and placing the answer over the denominator of 5. This provides an answer of 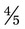image. 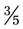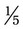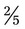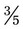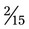To subtract image − image, subtract 1 from 3 [3 – 1]/5 for an answer of image).



Finding Common Denominators


For denominators to be the same for adding or subtracting fractions, the lowest common denominator, must be found. The smallest whole number that can be divided evenly by the denominators within the problem is the common denominator. Sometimes the lowest common denominator is easily found because one denominator is readily divided by the other denominator. For example, a common denominator for image + image could easily be found because 15 is divisible by 5. To change 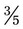image to the common denominator, divide the denominator 5 into the denominator 15 (3); then multiply the 3 (numerator) times 3 to calculate 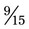image. 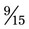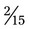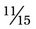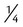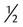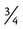Therefore image + image would provide an answer of image.



Tech Note


When estimating fractions, use 0, image, image, image, 1, and so on to estimate the answer with any calculations with fractions. Estimate either slightly larger or slightly smaller numbers. Remember that this is an estimate not a specific answer. It is for comparison for your exact answer.



Learning Tip


Estimation, even if mentally calculated, is important in accuracy with calculation of doses and dosages later. Please practice this as you go through this section as means to be sure your answer is reasonable. First estimate, then compute, and then check your answer to the estimation.


To change fractions to their equivalent fractions for adding or subtracting of fractions, first find the lowest common denominator and divide the denominator of the fraction to be changed into the lowest common denominator. Then multiply the numerator of the fraction being changed by the quotient found in the first step. Finally, place the product or answer found in this step over the lowest common denominator. 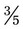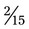In the previous example, in image + image, the lowest common denominator is 15. 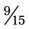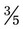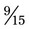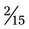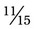The problem with the common denominator is image (15 ÷ 5 = 3; 3 × 3 = 9; so image = image) + image = image.



Example 2-9


310+35=?


image
< div class='tao-gold-member'>

Related posts:

  1. Assessment of Mathematical Calculation Skills Needed for Pharmacy Technicians
  2. Calculation of Medications Used Intravenously
  3. Interpretation of Medication Labels and Orders
  4. Calculate Doses of Oral and Parenteral Liquid Medications

Stay updated, free articles. Join our Telegram channel
Tags:
Jun 24, 2016 | Posted by in PHARMACY | Comments Off on Review of Basic Mathematical Skills

Full access? Get Clinical Tree
Get Clinical Tree app for offline access