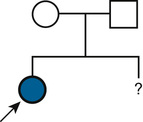
In contrast to single-gene disorders, the underlying mechanisms of inheritance for most chromosomal or genomic disorders and complex traits are unknown, and estimates of recurrence risk are based on previous experience (Fig. 16-2). This approach to risk assessment is valuable if there are reliable data on the frequency of recurrence of the disorder in families and if the phenotype is not heterogeneous. However, when a particular phenotype has an undetermined risk or can result from a variety of causes with different frequencies and with widely different risks, estimation of the recurrence risk is hazardous at best. In a later section, the estimation of recurrence risk in some typical clinical situations, both straightforward and more complicated, is considered.
Risk Estimation by Use of Mendel’s Laws When Genotypes Are Fully Known
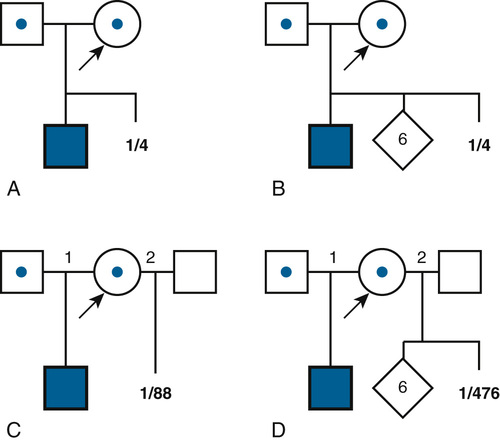
The simplest risk estimates apply to families in which the relevant genotypes of all family members are known or can be inferred. For example, if both members of a couple are known to be heterozygous carriers of an autosomal recessive condition because they have a child with the disorder or because of carrier testing, the risk (probability) is one in four with each pregnancy that the child will inherit two mutant alleles and inherit the disease (Fig. 16-3A). Even if the couple were to have six unaffected children subsequent to the affected child (Fig. 16-3B), the risk in the eighth, ninth, or tenth pregnancy would still be one in four for each pregnancy (assuming there is no misattributed paternity for the first affected child).
Risk Estimation by Use of Conditional Probability When Alternative Genotypes Are Possible
In contrast to the simple case just described, situations arise in which the genotypes of the relevant individuals in the family are not definitively known; the risk for recurrence will be very different, depending on whether or not the consultand is a carrier of an abnormal allele of a disease gene. For example, the chance that a woman, who is known from her first marriage to be a carrier of cystic fibrosis (CF), might have an affected child depends on the chance that her husband by her second marriage is a carrier (Fig. 16-3C). The risk for the partner’s being a carrier depends on his ethnic background (see Chapter 9). For the general non-Hispanic white population, this chance is approximately 1 in 22. Therefore the chance that a known carrier and her unrelated partner would have an affected first child is the product of these probabilities, or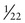 
× 
= 
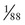(approximately 1.1%).
Of course, if the husband really were a carrier, the chance that the child of two carriers would be a homozygote or a compound heterozygote for mutant CF alleles is one in four. If the husband were not a carrier, then the chance of having an affected child is zero. Suppose, however, that one cannot test his carrier status directly. A carrier risk of 1 in 22 is the best estimate one can make for individuals of his ethnic background and no family history of CF without direct carrier testing; in fact, however, a person either is a carrier or is not. The problem is that we do not know. In this situation, the more opportunities the male in Figure 16-3C (who may or may not be a carrier of a mutant gene) has to pass on the mutant gene and fails to do so, the less likely it would be that he is indeed a carrier. Thus, if the couple were to come for counseling already with six children, none of whom is affected (Fig. 16-3D), it would seem reasonable, intuitively, that the husband’s chance of being a carrier should be less than the 1 in 22 risk that the childless male partner in Figure 16-3C was assigned on the basis of the population carrier frequency. In this situation, we apply conditional probability (also known as Bayesian analysis, based on Bayes’s theorem on probability published in 1763), a method that takes advantage of phenotypic information in a pedigree to assess the relative probability of two or more alternative genotypic possibilities and to condition the risk on the basis of that information. In Figure 16-3D, the chance that the second husband is a carrier is actually 1 in 119, and the chance that this couple would have a child with CF is therefore 1 in 476, not 1 in 88, as calculated in Fig. 16-3C. Some examples of the use of Bayesian analysis for risk assessment in pedigrees are examined in the following section.
Conditional Probability
To illustrate the application of Bayesian analysis, consider the pedigrees shown in Figure 16-4. In Family A, the mother II-1 is an obligate carrier for the X-linked bleeding disorder hemophilia A because her father was affected. Her risk for transmitting the mutant factor VIII (F8) allele responsible for hemophilia A is 1 in 2, and the fact that she has already had four unaffected sons does not reduce this risk. Thus the risk that the consultand (III-5) is a carrier of a mutant F8 allele is 1 in 2 because she is the daughter of a known carrier.
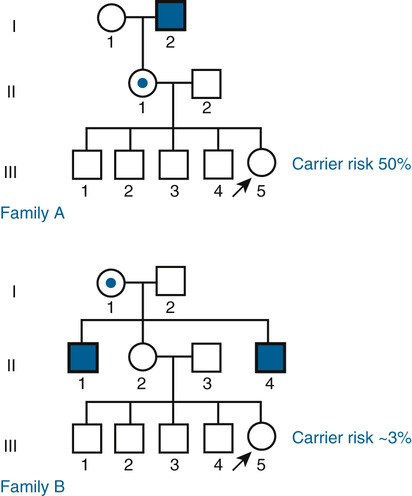
In Family B, however, the consultand’s mother (individual II-2) may or may not be a carrier, depending on whether she has inherited a mutant F8 allele from her mother, I-1. If III-5 were the only child of her mother, III-5’s risk for being a carrier would be 1 in 4, calculated as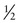 
(her mother’s risk for being a carrier) × 
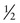(her risk for inheriting the mutant allele from her mother). Short of testing III-5 directly for the mutant allele, we cannot tell whether she is a carrier. In this case, however, the fact that III-5 has four unaffected brothers is relevant because every time II-2 had a son, the chance that the son would be unaffected is only 1 in 2 if II-2 were a carrier, whereas it is a near certainty (probability = 1) that the son would be unaffected if II-2 were, in fact, not a carrier at all. With each son, II-2 has, in effect, tested her carrier status by placing herself at a 50% risk for having an affected son. To have four unaffected sons might suggest that maybe her mother is not a carrier. Bayesian analysis allows one to take this kind of indirect information into account in calculating whether II-2 is a carrier, thus modifying the consultand’s risk for being a carrier. In fact, as we show in the next section, her carrier risk is far lower than 50%.
Identify the Possible Scenarios
To translate this intuition into actual risk calculation, we use a Bayesian probability calculation. First, we list all possible alternative genotypes that may be present in the relevant individuals in the pedigree (Fig. 16-5). In this case, there are three scenarios, each reflecting a different combination of alternative genotypes:
A. II-2 is a carrier, but the consultand is not.
B. II-2 and the consultand are both carriers.
C. II-2 is not a carrier, which implies that the consultand could not be one either because there is no mutant allele to inherit.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
