Tests for positive trend
Control-high pairwise comparisons (one-tailed)
Standard 2-year studies with 2 species and 2 sexes
Common and rare tumors are tested at 0. 005 and 0. 025 significance levels, respectively
Common and rare tumors are tested at 0. 01 and 0. 05 significance levels, respectively
Alternative ICH studies (one 2-year study in one species and one short- or medium- term study, two sexes)
Common and rare tumors are tested at 0. 01 and 0. 05 significance levels respectively
Under development and not yet available
However, this goal has not been universally accepted. There is a desire on the part of some non-statistical scientists within the agency to restrict positive findings to those where there is statistical evidence of both a positive dose response relationship and an increased incidence in the high dose group compared to the control group. In other words, a joint test is desired. This is not an intrinsically unreasonable position. Nonetheless, every test needs significance thresholds, and since the only significance thresholds included in US Food and Drug Administration—Center for Drug Evaluation and Research (2001) are for single tests, it is natural (but incorrect!) for non-statistical scientists to construct a joint test using these thresholds. We will refer to this decision rule as the joint test rule. See Table 12.2.
Table 12.2
The joint test rule (not recommended!)
Trend test | Pairwise test | |
|---|---|---|
Rare tumor | 0.025 | 0.050 |
Common tumor | 0.005 | 0.010 |
We are very concerned about the ramifications of the use of this rule. While the trend and pairwise test are clearly not independent, their association is far from perfect. Accordingly, the requirement that both tests yield individually statistically significant results necessarily results in a more conservative test than either the trend test or the pairwise test alone (at the same significance thresholds). The purpose of this section is to present the results of our simulation study showing a serious consequence of the adoption of this rule: a huge inflation of the false negative rate (i.e., the consumer’s risk) for the final interpretation of the carcinogenicity potential of a new drug.
12.2.2 Design of Simulation Study
The objective of this study is to conduct a simulation study to evaluate the inflation of the false negative rate resulting from the joint test (compared with the trend test alone).
We modeled survival and tumor data using Weibull distributions (see Eqs. (12.1) and (12.2)). The values of the parameters A, B, C, and D, were taken from the landmark National Toxicology Program (NTP) study by Dinse (1985) (see Tables 12.3 and 12.4). Values of these parameters were chosen to vary four different factors, ultimately resulting in 36 different sets of simulation conditions.
Model description | Weibull parameters | |||||||
|---|---|---|---|---|---|---|---|---|
Simulation conditions | Background tumor rate | Tumor appearancea | Dose effectb,c | A | B | C | D | |
1, 13, 25 | Low | 0.05 | Early | None | 17 | 2 | 6. 78 × 10−6 | 0 |
2, 14, 26 | Low | 0.05 | Early | Small | 17 | 2 | 6. 78 × 10−6 | 7. 36 × 10−6 |
3, 15, 27 | Low | 0.05 | Early | Large | 17 | 2 | 6. 78 × 10−6 | 1. 561 × 10−5 |
4, 16, 28 | Low | 0.05 | Late | None | 56 | 3 | 4. 65 × 10−7 | 0 |
5, 17, 29 | Low | 0.05 | Late | Small | 56 | 3 | 4. 65 × 10−7 | 5. 025 × 10−7 |
6, 18, 30 | Low | 0.05 | Late | Large | 56 | 3 | 4. 65 × 10−7 | 1. 0675 × 10−6 |
7, 19, 31 | High | 0.20 | Early | None | 21 | 2 | 3. 24 × 10−5 | 0 |
8, 20, 32 | High | 0.20 | Early | Small | 21 | 2 | 3. 24 × 10−5 | 9. 7 × 10−6 |
9, 21, 33 | High | 0.20 | Early | Large | 21 | 2 | 3. 24 × 10−5 | 2. 09 × 10−5 |
10, 22, 34 | High | 0.20 | Late | None | 57 | 3 | 2. 15 × 10−6 | 0 |
11, 23, 35 | High | 0.20 | Late | Small | 57 | 3 | 2. 15 × 10−6 | 6. 45 × 10−7 |
12, 24, 36 | High | 0.20 | Late | Large | 57 | 3 | 2. 15 × 10−6 | 1. 383 × 10−6 |
Weibull parameters | |||||
|---|---|---|---|---|---|
Simulation conditions | Drug effect on deatha,b | A | B | C | D |
1–12 | None | 0 | 4 | 3. 05 × 10−9 | 0 |
13–24 | Small | 0 | 4 | 3. 05 × 10−9 | 2. 390 × 10−9 |
25–36 | Large | 0 | 4 | 3. 05 × 10−9 | 8. 325 × 10−9 |
The factors used in the NTP study were defined as follows:
1.
Low or high tumor background rate: The prevalence rate at 2 years in the control group is 5 % (low) or 20 % (high).
2.
Tumors appear early or late: The prevalence rate of the control group at 1.5 years is 50 % (appearing early) or 10 % (appearing late) of the prevalence rate at 2 years.
3.
No dose effect, a small dose effect, or a large dose effect on tumor prevalence: The prevalence of the high dose group at 2 years minus the prevalence of the control group at 2 years is 0 % (no effect), or 10 % (small effect), or 20 % (large effect).
4.
No dose effect, a small dose effect, or a large dose effect on mortality: The expected proportion of animals alive in the high dose group at 2 years is 70 % (no effect), 40 % (small effect), or 10 % (large effect). The expected proportion of animals alive in the control group at 2 years is taken as 70 %.
However, there are important differences between the NTP design described above and the design used in our simulation study. Whereas the NTP study simulated three treatment groups with doses x = 0, x = 1, and x = 2 (called the control, low, and high dose groups), our study used four treatment groups (with doses x = 0, x = 1, x = 2, and x = 3, called the control, low, mid, and high dose groups respectively). Since the values of the parameters A, B, C, and D used were the same in the two studies (see Tables 12.3 and 12.4), the characterizations of the effect of the dose level on tumorigenesis and mortality, factors 3 and 4, apply to the dose level x = 2, i.e., to the mid dose level. To recast these descriptions in terms of the effect at the x = 3 (high dose) level, factors 3 and 4 become factors 3′ and 4′:
3′
No dose effect, a small dose effect, or a large dose effect on tumor prevalence: The prevalence of the high dose group at 2 years minus the prevalence of the control group at 2 years is 0 % (no effect), or approximately 15 % (small effect), or approximately 28 % (large effect).
4′
No dose effect, a small dose effect, or a large dose effect on mortality: The expected proportion of animals alive in the high dose group at 2 years is 70 % (no effect), 30 % (small effect), or 4 % (large effect). The expected proportion of animals alive in the control group at 2 years is taken as 70 %.
These differences can be expected to have the following effects on the Type 2 error rates for our study (relative to the NTP study):
The higher tumorigenesis rates in the high dose groups should help to reduce the false negative rates (or to increase the levels of power) of statistical tests.
On the other hand, higher levels of mortality will reduce the effective sample size and thus tend to increase the false negative rates (or to decrease the levels of power).1
In our study, tumor data were generated for 4 treatment groups with equally spaced increasing doses (i.e., x = 0, x = 1, x = 2, and x = 3). There were 50 animals per group. The study duration was 2 years (104 weeks), and all animals surviving after 104 weeks were terminally sacrificed. All tumors were assumed to be incidental.
The tumor detection time (T 0) (measured in weeks) and the time to natural death (T 1) of an animal receiving dose level x were modeled by four parameter Weibull distributions:
The prevalence function for incidental tumors equals the cumulative function of time to tumor onset, i.e.,
![$$\displaystyle{ P(t\vert x) =\Pr [T_{0} \leq t\vert X = x] = 1 - S(t,x). }$$](/wp-content/uploads/2016/07/A330233_1_En_12_Chapter_Equ2.gif)
![$$\displaystyle{ P(t\vert x) =\Pr [T_{0} \leq t\vert X = x] = 1 - S(t,x). }$$](/wp-content/uploads/2016/07/A330233_1_En_12_Chapter_Equ2.gif)
(12.2)
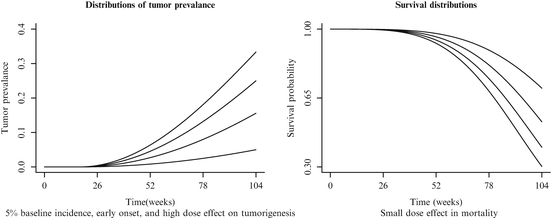
Each of the 36 simulation conditions described in Tables 12.3 and 12.4 was simulated 10,000 times. For each simulation, 200 animals were generated; each animal was assigned to a dose group (50 animals per group) and had a tumor onset time (T 0) and death time (T 1) simulated using Eq. (12.1). The actual time of death (T) for each animal was defined as the minimum of T 1 and 104 weeks, i.e., 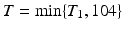 . The animal developed the tumor (i.e., became a tumor bearing animal (TBA)) only if the time to tumor onset did not exceed the time to death. The actual tumor detection time was assumed to be the time of death T. Animals in the same dose group were equally likely to develop the tumor in their life times. It was assumed that tumors were developed independently of each other. The first panel of Fig. 12.1 graphically represents the Weibull models used to generate the tumor prevalence data when the background tumor rate is low, the dose effect on tumor prevalence is large, and the tumor appears early (the model used in simulation conditions 3, 15, and 27). The second panel graphically represents the Weibull models used to generate the survival data when the dose effect on mortality is small (simulation conditions 13–24). The age-adjusted Peto method to test for a dose response relationship (Peto et al. 1980) and the age adjusted Fisher exact test for pairwise differences in tumor incidence, (in each case using the NTP partition of time intervals2), were applied to calculate p-values.
. The animal developed the tumor (i.e., became a tumor bearing animal (TBA)) only if the time to tumor onset did not exceed the time to death. The actual tumor detection time was assumed to be the time of death T. Animals in the same dose group were equally likely to develop the tumor in their life times. It was assumed that tumors were developed independently of each other. The first panel of Fig. 12.1 graphically represents the Weibull models used to generate the tumor prevalence data when the background tumor rate is low, the dose effect on tumor prevalence is large, and the tumor appears early (the model used in simulation conditions 3, 15, and 27). The second panel graphically represents the Weibull models used to generate the survival data when the dose effect on mortality is small (simulation conditions 13–24). The age-adjusted Peto method to test for a dose response relationship (Peto et al. 1980) and the age adjusted Fisher exact test for pairwise differences in tumor incidence, (in each case using the NTP partition of time intervals2), were applied to calculate p-values.
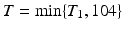 . The animal developed the tumor (i.e., became a tumor bearing animal (TBA)) only if the time to tumor onset did not exceed the time to death. The actual tumor detection time was assumed to be the time of death T. Animals in the same dose group were equally likely to develop the tumor in their life times. It was assumed that tumors were developed independently of each other. The first panel of Fig. 12.1 graphically represents the Weibull models used to generate the tumor prevalence data when the background tumor rate is low, the dose effect on tumor prevalence is large, and the tumor appears early (the model used in simulation conditions 3, 15, and 27). The second panel graphically represents the Weibull models used to generate the survival data when the dose effect on mortality is small (simulation conditions 13–24). The age-adjusted Peto method to test for a dose response relationship (Peto et al. 1980) and the age adjusted Fisher exact test for pairwise differences in tumor incidence, (in each case using the NTP partition of time intervals2), were applied to calculate p-values.
. The animal developed the tumor (i.e., became a tumor bearing animal (TBA)) only if the time to tumor onset did not exceed the time to death. The actual tumor detection time was assumed to be the time of death T. Animals in the same dose group were equally likely to develop the tumor in their life times. It was assumed that tumors were developed independently of each other. The first panel of Fig. 12.1 graphically represents the Weibull models used to generate the tumor prevalence data when the background tumor rate is low, the dose effect on tumor prevalence is large, and the tumor appears early (the model used in simulation conditions 3, 15, and 27). The second panel graphically represents the Weibull models used to generate the survival data when the dose effect on mortality is small (simulation conditions 13–24). The age-adjusted Peto method to test for a dose response relationship (Peto et al. 1980) and the age adjusted Fisher exact test for pairwise differences in tumor incidence, (in each case using the NTP partition of time intervals2), were applied to calculate p-values.
Fig. 12.1
Sample tumor prevalence and mortality curves
Three rules for determining if a test of the drug effect on development of a given tumor type was statistically significant were applied to the simulated data. They were:
1.
Requiring a statistically significant result in the trend test alone. This is the rule recommended in US Food and Drug Administration—Center for Drug Evaluation and Research (2001).
2.
Requiring statistically significant results both in the trend test and in any of the three pairwise comparison tests (control versus low, control versus medium, control versus high).
3.
Requiring statistically significant results both in the trend test and in the control versus high group pairwise comparison test. This is the joint test rule.
In each case, it was assumed that the tests were being conducted as part of a standard two-species study. The rules for rare tumor types were used when the incidence rate in the control group were below 1%; otherwise the rules for common tumors types were used.
After simulating and analyzing tumor data 10,000 times for each of the 36 sets of simulation conditions, the Type 1 and Type 2 error rates were estimated.
12.2.3 Results of the Simulation Study
Since we are simultaneously considering both models where the null hypothesis is true (so that there is no genuine dose effect on tumor incidence) and models where it is false (where there is a genuine dose effect), we need terminology that can apply equally well to both of these cases. For any given set of simulation conditions, the retention rate is the probability of retaining the null hypothesis. If the null hypothesis is true, then this rate is the probability of a true negative, and is 1 − thefalsepositiverate (Type I error). If the null hypothesis is false, then the retention rate is the probability of a false negative or Type 2 error. In this case, it is 1 − power. Correspondingly, the rejection rate is 1 − theretentionrate, and is the probability that the null hypothesis is rejected. It is either the false positive rate (if the null hypothesis is true) or the level of power (if the alternative hypothesis is true). The results (retention rates and percent changes of retention rates) of the simulation study are presented in Table 12.5.
Table 12.5
Estimated retention rates under three decision rules
Simulation condition | Simulation condition properties | Retention probabilities | % Change in retention rate | ||||||
|---|---|---|---|---|---|---|---|---|---|
Dose effect on mortality | Tumor appearance time | Dose effect on tumor prevalence | Tumor background rate | Trend test only | Trend test and H/C | Trend test and any pairwise | Trend test and H/C | Trend test and any pairwise | |
1 | No | Early | No | 0.05 | 0.984 | 0.9934 | 0.9919 | 0.9553 | 0.8028 |
2 | No | Early | Small | 0.05 | 0.6283 | 0.7084 | 0.6957 | 12.75 | 10.73 |
3 | No | Early | Large | 0.05 | 0.1313 | 0.178 | 0.1595 | 35.57 | 21.48 |
4 | No | Late | No | 0.05 | 0.9827 | 0.9927 | 0.9915 | 1.018 | 0.8955 |
5 | No | Late | Small | 0.05 | 0.6314 | 0.7208 | 0.7076 | 14.16 | 12.07 |
6 | No | Late | Large | 0.05 | 0.1408 | 0.2018 | 0.1811 | 43.32 | 28.62 |
7 | No | Early | No | 0.2 | 0.9953 | 0.9979 | 0.9974 | 0.2612 | 0.211 |
8 | No | Early | Small | 0.2 | 0.8377 | 0.8805 | 0.8715 | 5.109 | 4.035 |
9 | No | Early | Large | 0.2 | 0.3424 | 0.427 | 0.398 | 24.71 | 16.24 |
10 | No | Late | No | 0.2 | 0.9952 | 0.9972 | 0.9972 | 0.201 | 0.201 |
11 | No | Late | Small | 0.2 | 0.8399 | 0.8869 | 0.8772 | 5.596 | 4.441 |
12 | No | Late | Large | 0.2 | 0.3754 | 0.4864 | 0.4565 | 29.57 | 21.6 |
13 | Small | Early | No | 0.05 | 0.9855 | 0.9985 | 0.9978 | 1.319 | 1.248 |
14 | Small | Early | Small | 0.05 | 0.6967 | 0.8465 | 0.8324 | 21.5 | 19.48 |
15 | Small | Early | Large | 0.05 | 0.2152 | 0.4112 | 0.3574 | 91.08 | 66.08 |
16 | Small | Late | No | 0.05 | 0.9819 | 0.9991 | 0.9977 | 1.752 | 1.609 |
17 | Small | Late | Small | 0.05 | 0.722 | 0.9161 | 0.8903 | 26.88 | 23.31 |
18 | Small | Late | Large | 0.05 | 0.2682 | 0.6794 | 0.6021 | 153.3 | 124.5 |
19 | Small | Early | No | 0.2 | 0.9948 | 0.9996 | 0.9995 | 0.4825 | 0.4725 |
20 | Small | Early | Small | 0.2 | 0.8753 | 0.9694 | 0.9606 | 10.75 | 9.745 |
21 | Small | Early | Large | 0.2 | 0.4649 | 0.7564 | 0.711 | 62.7 | 52.94 |
22 | Small | Late | No | 0.2 | 0.9961 | 0.9999 | 0.9996 | 0.3815 | 0.3514 |
23 | Small | Late | Small | 0.2 | 0.8935 | 0.9939 | 0.9885 | 11.24 | 10.63 |
24 | Small | Late | Large | 0.2 | 0.538 | 0.9455 | 0.9095 | 75.74 | 69.05 |
25 | Large | Early | No | 0.05 | 0.9856 | 0.9994 | 0.9989 | 1.4 | 1.349 |
26 | Large | Early | Small | 0.05 | 0.8381 | 0.9587 | 0.948 | 14.39 | 13.11 |
27 | Large | Early | Large | 0.05 | 0.5358 | 0.8133 | 0.7796 | 51.79 | 45.5 |
28 | Large | Late | No | 0.05 | 0.9828 | 1 | 1 | 1.75 | 1.75 |
29 | Large | Late | Small | 0.05 | 0.8675 | 0.996 | 0.9886 | 14.81 | 13.96 |
30 | Large | Late | Large | 0.05 | 0.6447 | 0.9807 | 0.9428 | 52.12 | 46.24 |
31 | Large | Early | No | 0.2 | 0.994 | 1 | 1 | 0.6036 | 0.6036 |
32 | Large | Early | Small | 0.2 | 0.9414 | 0.9994 | 0.9985 | 6.161 | 6.065 |
33 | Large | Early | Large | 0.2 | 0.7445 | 0.9823 | 0.97 | 31.94 | 30.29 |
34 | Large | Late | No | 0.2 | 0.9956 | 1 | 1 | 0.4419 | 0.4419 |
35 | Large | Late | Small | 0.2 | 0.9585 | 1 | 0.9999 | 4.33 | 4.319 |
36 | Large | Late | Large | 0.2 | 0.835 | 0.9998 | 0.9989 | 19.74 | 19.63 |
Results of the evaluation of Type 1 error patterns in the study conducted and reported in Dinse (1985) show that the Peto test without continuity correction and with the partition of time intervals of the study duration proposed by NTP (see Footnote 2) yields attained false positive rates close to the nominal levels (0. 05 and 0. 01) used in the test. That means that the test is a good one that is neither conservative nor anti-conservative.
The evaluation of Type 1 error patterns found by this simulation study is done by using the rates at which the null hypothesis was rejected under those simulation conditions for which there was no dose effect on tumor rate (simulation conditions 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, and 34 in Table 12.5). The tumor types were classified as rare or common based on the incidence rate of the concurrent control. The results of this simulation study show a very interesting pattern in levels of attained Type 1 error. The attained levels of Type 1 error under various simulation conditions divided into two groups. The division was by the factor of background rate, either 20 or 5 %. The attained Type1 levels of the first group were around 0. 005. The attained Type 1 error rates for the second group were around 0. 015. The observed results and pattern of the attained Type 1 errors make sense. For the simulated conditions with 20 % background rate, probably almost all of the 10,000 generated datasets (each dataset containing tumor and survival data of four treatment groups of 50 animals each group) will have a tumor rate of equal to or greater than 1 % (the definition of a common tumor) in the control group. The attained levels of Type 1 error rates under various simulated conditions in this group are close to the nominal significance levels for common tumors.3
The attained Type 1 error rates for the other group were between the nominal levels of significance of 0.005 (for the trend test for common tumors) and 0.025 (for the trend test for rare tumors) and not around 0.005. The reason for this phenomenon is that, though the background rate in the simulated conditions for this group was 5 % that is considered as a rate for a common tumor, some of the 10,000 generated datasets had tumor rates less than 1 % in the control group. For this subset of the 10,000 datasets, the nominal level of 0.025 was used in the trend test. See Sect. 12.3.4.3 for a more detailed discussion of this factor.
As mentioned previously, the main objective of our study is the evaluation of the Type 2 error rate under various conditions. As was expected, the Type 2 error (or false negative) rates resulting from the joint test decision rule are higher than those from the procedure recommended in the guidance document of using trend test alone. This is due to the fact that in statistical theory the false positive rate (measuring the producer’s risk in the regulatory review of toxicology studies) and the false negative rate (measuring the consumer’s risk) run in the opposite direction; use of the joint test decision rule will cut down the former rate only at the expense of inflating the latter rate.
The estimated false negative rates resulting from the extensive simulation study under the three decision rules listed in Sect. 12.2.2 are shown in Table 12.5. The last two columns of the table show the percentage changes in the retention rates of decision rules (2) and (3) respectively, compared to those of (1). For those simulation conditions where the null hypothesis is true (1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, and 34), these values measure the percentage change in the probability of not committing a Type 1 error. For the remaining simulation conditions, these values measure the inflation of the Type 2 error rate attributable to the adoption of the more stringent rules.
The magnitude of the inflation of false negative rate resulting from the joint test decision rule of requiring statistically significant results in both the trend test and the C-H (High versus Control) pairwise comparison test depends on all the four factors, namely, drug effect on mortality, background tumor rate, time of tumor appearance, and drug effect on tumor incidence considered in the simulation that are also listed in the notes at the bottom of Tables 12.3 and 12.4.
12.2.4 Discussion
Results of the simulation study show that the factor of the effect of the dose on tumor prevalence rates has the largest impact on the inflation of the false negative rate when both the trend test and the C-H pairwise comparison tests are required to be statistically significant simultaneously in order to conclude that the effect is statistically significant. The inflations are most serious in the situations in which the dose has a large effect on tumor prevalence. The inflation can be as high as 153.3 %. The actual Type 2 error rate can be more than double.
The above finding is the most alarming result among those from our simulation study. When the dose of a new test drug has large effects on tumor prevalence (up to 28 % difference in incidence rates between the high dose and the control groups), it is a clear indication that the drug is carcinogenic. Exactly in these most important situations the joint test decision rule causes the most serious inflations of the false negative error rate (or the most serious reductions in statistical power to detect the true carcinogenic effect). The net result of this alarming finding is that using the levels of significance recommended for the trend test alone and the pairwise test alone in the joint test decision rule can multiply the probability of failure to detect a true carcinogenic effect by a factor up to two or even more, compared with the procedure based on the result of the trend test alone.
It is true that the results in Table 12.5 show that, for the situations in which the dose has a small effect (up to 15 % difference in incidence rates between the high dose and the control groups) on tumor prevalence, the increases of false negative rates caused by the joint test decision rule are not much more than those from using the trend test alone (increases can be up to 27 %). However, this observation does not imply that the joint test decision rule is justified. The reason is that standard carcinogenicity studies use small group sizes as a surrogate for a large population with low tumor incidence. There is very little power (i.e., the false negative rates are close to 100 %) for a statistical test using a small level of significance such as 0.005 to detect any true carcinogenicity effect because of low tumor incidence rates. In those situations there will be little room for the further increase in the false negative rate no matter how many additional tests are put on top of the original trend test.
It might be argued that the large inflations in false negative rates in the use of the joint test over the use of the trend test alone could be due to the large dose effect on death (only 4 % animals alive at 2 years introduced by the additional treatment group with x = 3. The argument may sound valid since as mentioned previously, the decrease of percentage of animals alive at 2 years increases the false negative rates. We are aware of the small number of alive animals at 2 years in the simulation condition of large dose effect on death caused by using the built-in Weibull model described in Dinse (1985) and by including the additional group with x = 3 in the our study.
However, as mentioned previously, our main interest in this study is to evaluate the percentages of inflation in false negative rates attributable to the use of the joint test compared with the trend test alone. The false negative rates in the joint test and in the trend test alone are certainly also of our interest. They are not the main interest. So the issue of excessive mortality under the simulation condition of a large dose effect on death should not be a major issue in this study since it has similar impacts on false negative rates in both the joint test and the trend test alone. Furthermore, it is seen from Table 12.5 that the largest inflations (63–153 %) in the false negative rate happened under the conditions in which the dose effect on death is small (30 % alive animals at 2 years) rather than under the condition in which the effect is large (4 % alive animals at 2 years).
The extremely large false negative rates in the above simulated situations caused by the nature (low cancer rates and small group sample sizes) of a carcinogenicity experiment, reinforce the important arguments that it is necessary to allow an overall (for a compound across studies in two species and two sexes) false positive rate of about 10 % to raise the power (or to reduce the false negative rate) of an individual statistical test. This important finding of the simulation study clearly supports our big concern about failing to detect carcinogenic effects in the use of the joint test decision rule in determining the statistical significance of the carcinogenicity of a new drug. Again, the producer’s risk using a trend alone is known at the level of significance used (0.5 % for a common tumor and 2.5 % for a rare tumor in a two-species study) and is small in relation to the consumer’s risk that can be 100 or 200 times the level of the known producer’s risk. The levels of significance recommended in the guidance for industry document were developed with the consideration of those situations in which the carcinogenicity experiment has great limitations. Trying to cut down only the producer’s risk (false positive rate in toxicology studies) beyond that which safeguards against the huge consumer’s risk (false negative rates in toxicology studies) is not consistent with the FDA mission as a regulatory agency that has the duty to protect the health and well-being of the American general public.
As mentioned previously, the decision rules (levels of significance) recommended in US Food and Drug Administration—Center for Drug Evaluation and Research (2001) are for trend tests alone and for pairwise comparisons alone, and not for the joint test. To meet the desire of some non-statistical scientists within the agency to require statistically significant results for both the trend test and the C-H pairwise comparison simultaneously to conclude that the effect on the development of a given tumor/organ combination as statistically significant, and still to consider the special nature of standard carcinogenicity studies (i.e., using small group sizes as a surrogate of a large population with low a tumor incidence endpoint), we have conducted additional studies and proposed new sets of significance levels for a joint test along with some updates of the previously recommended ones. These are presented in Table 12.6. We have found that the use of these new levels keeps the overall false positive rate (for the joint test) to approximately 10 % again for a compound across studies in two species and two sexes.
Table 12.6
Recommended decision rules (levels of significance) for controlling the overall false positive rates for various statistical tests performed and submission types
Decision rule | ||||||
|---|---|---|---|---|---|---|
Joint test | ||||||
Submission type | Tumor type | Trend test alone | Pairwise test alone | Trend test | Pairwise test | |
Standard 2 year study with two sexes and two species | Common | 0.005 | 0.01 | 0.005 | 0.05 | |
Rare | 0.025 | 0.05 | 0.025 | 0.10 | ||
Alternative ICH Studies (One 2-year study in one species and one short- or medium-term alternative study, two sexes) | Two-year study | Common | 0.005 | 0.01 | 0.005 | 0.05 |
Rare | 0.025 | 0.05 | 0.025 | 0.10 | ||
Short- or medium-term alternative study | Common | 0.05 | 0.05 | 0.05 | 0.05 | |
Rare | 0.05 | 0.05 | 0.05 | 0.05 | ||
Standard 2 year studies with two sexes and one species | Common | 0.01 | 0.025 | 0.01 | 0.05 | |
Rare | 0.05 | 0.10 | 0.05 | 0.10 | ||
12.3 The Relationship Between Experimental Design and Error Rates
In this section, we describe the results of a second simulation study. The aim of the simulation study discussed in Sect. 12.2 was to compare decision rules, evaluating the impact on error rates of the adoption of the joint test rule (which is more conservative than the trend test rule recommended in US Food and Drug Administration—Center for Drug Evaluation and Research (2001)—see Tables 12.1 and 12.2). By contrast, this second study, which was conducted independently, compares the effects of the use of different experimental designs on the error rates, all under the same decision rule. The decision rule used in this study is the joint test rule (Table 12.2) since, despite the absence of any theoretical justification for its use, this rule is currently used by non-statistical scientists within the agency as the basis for labeling and other regulatory decisions.4
We first consider the nature of the various hypotheses under consideration, and the associated error rates (Sect. 12.3.1). This provides us with the terminology to express our motivation (Sect. 12.3.2). We then describe in detail the four designs that have been compared (Sect. 12.3.3), and the simulation models used to test these designs (Sect. 12.3.4). The results of the simulation are discussed in Sects. 12.3.5 (power) and 12.3.6 (Type 1 error). We conclude with a brief discussion (Sect. 12.3.7).
12.3.1 Endpoints, Hypotheses, and Error Rates
The task of analyzing data from long term rodent bioassays is complicated by a severe multiplicity problem. But it is not quite the case that we are merely faced with a multitude of equally important tumor endpoints. Rather, we are faced with a hierarchy of hypotheses.
At the lowest level, we have individual tumor types, and some selected tumor combinations, associated with null hypotheses of the form:
Administration of the test article is not associated with an increase in the incidence rate of malignant astrocytomas of the brain in female rats.
We call such hypotheses the local null hypotheses.
The next level of the hierarchy is the experiment level. A standard study includes four experiments: on male mice, on female mice, on male rats, and on female rats. Each of these experiments is analyzed independently, leading to four global null hypotheses of the form:
There is no organ–tumor pair, or reasonable combination of organ-tumor pairs, for which administration of the test article is positively associated with tumorigenesis in male mice.
Note that some studies consist of just two experiments in a single species (or, very rarely, in two species and a single sex).
The highest level of the hierarchy of hypotheses is the study level. There is a single study-wise null hypothesis:
For none of the experiments conducted is the corresponding global null hypothesis false.
For any given local null hypothesis, the probability of rejecting that null hypothesis is called either the local false positive rate (LFPR) or the local power, depending on whether the null hypothesis is in fact true. If all the local null hypotheses in a given experiment are true, then the global false positive rate (GFPR) for that experiment is the probability of rejecting the global null hypothesis, and can be estimated from the various estimates for the LFPRs for the endpoints under consideration.5 The goal of the multiplicity adjustments in US Food and Drug Administration—Center for Drug Evaluation and Research (2001) is to maintain the study-wise false positive rate at about 10 %. Since most studies consist of four independent experiments, we consider our target level for false positives to be a GFPR of approximately 2.5 %.6
The calculation of a GFPR from the LFPR depends on the relationship between the local and global null hypotheses. We capture this relationship with the notion of a tumor spectrum: If 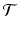 is the parameter space for tumor types, then a spectrum is a function
is the parameter space for tumor types, then a spectrum is a function 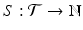 ; S(t) is the number of independent tumor types being tested with parameter value t. In our case,
; S(t) is the number of independent tumor types being tested with parameter value t. In our case,  is one dimensional: under the global null hypothesis we assume that each tumor can be characterized by its background prevalence rate.7
is one dimensional: under the global null hypothesis we assume that each tumor can be characterized by its background prevalence rate.7
 is the parameter space for tumor types, then a spectrum is a function
is the parameter space for tumor types, then a spectrum is a function 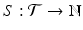 ; S(t) is the number of independent tumor types being tested with parameter value t. In our case,
; S(t) is the number of independent tumor types being tested with parameter value t. In our case, 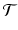 is one dimensional: under the global null hypothesis we assume that each tumor can be characterized by its background prevalence rate.7
is one dimensional: under the global null hypothesis we assume that each tumor can be characterized by its background prevalence rate.7 In our simulations, we generate estimates for the power and LFPR for three different classes of tumor:
1.
Rare tumors have a background prevalence rate (i.e., the lifetime incidence rate among those animals who do not die from causes unrelated to the particular tumor type before the end of the study, typically at 104 weeks) of 0. 5 %.
2.
Common tumors have a background prevalence rate of 2 %.
3.
Very common tumors have a background prevalence rate of 10 %.
A tumor spectrum for us therefore consists of a triple 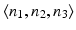 , indicating that the global null hypothesis is the conjunction of
, indicating that the global null hypothesis is the conjunction of 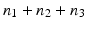 local null hypotheses, and asserts the absence of a treatment effect on tumorigenicity for n 1 rare, n 2 common, and n 3 very common independent tumor endpoints.
local null hypotheses, and asserts the absence of a treatment effect on tumorigenicity for n 1 rare, n 2 common, and n 3 very common independent tumor endpoints.
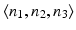 , indicating that the global null hypothesis is the conjunction of
, indicating that the global null hypothesis is the conjunction of 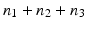 local null hypotheses, and asserts the absence of a treatment effect on tumorigenicity for n 1 rare, n 2 common, and n 3 very common independent tumor endpoints.
local null hypotheses, and asserts the absence of a treatment effect on tumorigenicity for n 1 rare, n 2 common, and n 3 very common independent tumor endpoints.Given such a spectrum, and under any given set of conditions, the GFPR is easy to calculate from the LFPR estimates for the three tumor types under those conditions:
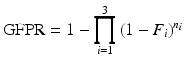
where F i is the estimated LFPR for the i-th class of tumors. Since our desired false positive rates are phrased in terms of the study-wise false positive rate (which we want to keep to a level of approximately 10 %), we are more concerned with the GFPR than the LFPR.
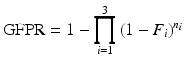
(12.3)
Global power is slightly harder to calculate, since it is a function of a specific global alternate hypothesis. It is unclear what a realistic global alternative hypothesis might look like, except that a global alternative hypothesis is likely to be the conjunction of a very small number of local alternative hypotheses with a large number of local null hypotheses. Accordingly, we focus our attention on the local power.
In summary then, the two quantities that we most wish to estimate are the local power and the GFPR.
12.3.2 Motivation
For any given experimental design, there is a clear and well understood trade-off between the Type 1 rate (the false positive rate) and the Type 2 error rate (1 minus the power): by adjusting the rejection region for a test, usually by manipulating the significance thresholds, the test can be made more or less conservative. A more conservative test has a lower false positive rate, but only at the expense of a higher Type 2 error rate (i.e., lower power), while a more liberal test lowers the Type 2 error rate at the cost of raising the Type 1 error rate. Finding an appropriate balance of Type 1 and Type 2 errors is an important part of the statistical design for an experiment, and requires a consideration of the relative costs of the two types of error. It is generally acknowledged (see Center for Drug Evaluation and Research 2005) that for safety studies this balance should prioritize Type 2 error control.
However, this trade-off applies only to a fixed experimental design; by adjusting the design, it may be possible to simultaneously improve both Type 1 and Type 2 error rates.8 Beyond this general principle, there is a particular reason to suspect that adjusting the design might affect error rates for carcinogenicity studies. It has been shown (Lin and Rahman 1998; Rahman and Lin 2008) that, using the trend test alone and the significance thresholds in Table 12.1, the study-wise false positive rate for rodent carcinogenicity studies is approximately 10 %. However, under this decision rule, the nominal false positive rate for a single rare tumor type is 2. 5 %. Given that each study includes dozens of rare endpoints, the tests must be strongly over-conservative for rare tumor types9; the decision rules in US Food and Drug Administration—Center for Drug Evaluation and Research (2001) rely heavily on this over-conservativeness in order to keep the GFPR to an acceptable level. But this sort of over-conservativeness is exactly the sort of phenomenon that one would expect to be quite sensitive to changes in study design.
12.3.3 Designs Compared
To get a sense of the designs currently in use, we conducted a brief investigation of 32 recent submissions, and drew the following general conclusions:
While most designs use a single vehicle control group, a substantial proportion do use two duplicate vehicle control groups.
A large majority of designs use three treated groups.
The total number of animals used can vary considerably, but is typically between 250 and 300.
The “traditional” design of four equal groups of 50 is still in use, but is not common; most designs use larger samples of animals.
Bearing these observations in mind, we compare four designs, outlined in Table 12.7. Three of these designs (D1–2 and D4) utilize the same number of animals (260), so that any effects due to differences in the disposition of the animals will not be obscured by differences due to overall sample size.
Table 12.7
Experimental designs considered
Number of animals per group | |||||
|---|---|---|---|---|---|
Design number | Control | Low | Mid | High | Total |
D1 | 65 | 65 | 65 | 65 | 260 |
D2 | 104 | 52 | 52 | 52 | 260 |
D3 | 50 | 50 | 50 | 50 | 200 |
D4 | 60 | 50 | 100 | 50 | 260 |
The first two designs, D1 and D2, are representative of designs currently in use. Design D1 uses four equal groups of 65 animals whereas design D2 uses a larger control group (104 animals) and three equal dose groups (52 animals each). This is equivalent to a design with five equal groups, comprising two identical vehicle control groups (which, since they are identical, may be safely combined) and three treated groups.
The third design tested (D3) is the “traditional” 200 animal design. Although D3 uses fewer animals than the other designs (but is otherwise similar to D1), it has been included to enable comparison with the many simulation studies and investigations which use this design, such as that described in Sect. 12.2, and in Dinse (1985), Portier and Hoel (1983), Lin and Rahman (1998), and Rahman and Lin (2008)
In light of the investigation (Jackson 2015) of the possible benefits of unbalanced designs (where the animals are not allocated equally to the various dose groups), we have also included an unbalanced design for comparison. This design (D4) follows the suggestions of Portier and Hoel (1983):
…we feel that a design with 50 to 60 of the experimental animals at control (d 0 = 0), 40 to 60 of the animals at the MTD (d 3 = 1) and the remaining animals allocated as one-third to a group given a dose of 10–30 % MTD (d 1 = 0. 25 seems best) and two-thirds to a group given a dose of 50 % MTD (d 2 = 0. 5). No less than 150 experimental animals should be used, and more than 300 animals is generally wasteful. An acceptable number of animals would be 200.
Accordingly, 60 animals have been allocated to the control group and 50 to the high dose group, with the remaining 150 animals allocated 2:1 to the mid and low dose groups.
12.3.4 Statistical Methodology
12.3.4.1 Simulation Schema
We have conducted two separate simulation studies. The first study was designed to compare the (local) power of the four designs to detect genuine increases in tumorigenicity for the three tumor types (rare, common, and very common) described in Sect. 12.3.1. In each case, about fifty different effect sizes (measured as the odds ratio for tumor incidence between a high dose and control animals at 104 weeks) were tested 1000 times. While 1000 simulations are not adequate to accurately estimate the power for a particular effect size (we can expect a margin of error in the estimate of approximately 3 %), we may still form an accurate impression of the general shape of the power curves.
The second simulation study was aimed at evaluating false positive (Type 1 error) rates. The immediate focus was on the LFPR, the rate at which individual organ-tumor endpoints for which there is no genuine effect are falsely found to be targets of a carcinogenic effect. Because local false positives are very rare, and because imprecision in the estimate of the local false positive rate is amplified when computing the global false positive rate, each simulation scenario has been repeated at least 250,000 times. The resulting estimates are amalgamated to compute the GFPR by appealing to independence and applying Eq. (12.3) to three different tumor spectra.
For both of the simulation studies, data were simulated using a competing risks model. The two competing hazards were tumorigenesis and death due to a non-tumor cause.
Since these simulations are intended to evaluate power and GFPRs under fairly optimal circumstances, only one toxicity model has been considered: the hazard function for non-tumor death has the form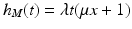 , where x is the dose and t is the time. The parameters
, where x is the dose and t is the time. The parameters  and μ are chosen so that the probabilities of a control animal and a high dose animal experiencing non-tumor death before the scheduled termination date are 0. 4 and 0. 7 respectively.
and μ are chosen so that the probabilities of a control animal and a high dose animal experiencing non-tumor death before the scheduled termination date are 0. 4 and 0. 7 respectively.
Tumor onset time is modeled according to the poly-3 assumptions. This means that for any given animal, the probability of tumorigenesis before time t has the form![$$P[T \leq t] =\lambda t^{3}$$](/wp-content/uploads/2016/07/A330233_1_En_12_Chapter_IEq12.gif) where the parameter
where the parameter  is a measure of the animal’s tumor risk, and so depends on the dose x, the background prevalence rate (i.e., the tumor incidence rate when x = 0), and the dose effect on tumorigenesis to be simulated. (In the case of the LFPR simulations, it is assumed that there is no dose effect on tumorigenesis, and
is a measure of the animal’s tumor risk, and so depends on the dose x, the background prevalence rate (i.e., the tumor incidence rate when x = 0), and the dose effect on tumorigenesis to be simulated. (In the case of the LFPR simulations, it is assumed that there is no dose effect on tumorigenesis, and  therefore depends on the background prevalence rate alone).
therefore depends on the background prevalence rate alone).
Although these simulations were devised independently of those in Sect. 12.2, the resulting models are in practice quite similar. Tumor onset times modeled by this approach are very similar to those of the “early onset” models, although non-tumor mortality times tend to be earlier than those simulated in Sect. 12.2. The effect of this difference is likely to be a small reduction in power (and LFPRs) in the present model compared with those used in Sect. 12.2.
12.3.4.2 Decision Rule
As noted above, we are initially concerned with estimating local power and LFPRs. Accordingly, under each scenario, we simulate data for a single 24 month experiment (male mice, for example), and a single tumor endpoint (cortical cell carcinoma of the adrenal gland, for example). Each set of simulated data includes a death time for each animal and information about whether the animal developed a tumor. From these data, two poly-3 tests (see Sect. 12.4 and Bailer and Portier 1988; Bieler and Williams 1993; US Food and Drug Administration—Center for Drug Evaluation and Research 2001) are conducted: a trend test across all groups, and a pairwise test between the control and high dose groups. As we are using the joint test rule (discussed at length in Sect. 12.2.1), the null hypothesis of no tumorigenic effect is rejected only when both the trend and pairwise tests yield individually significant results, at the levels indicated in Table 12.2.
12.3.4.3 Misclassification
The use of the observed incidence rate in the control group to classify a tumor as rare or common is potentially problematic. There is clearly a substantial likelihood that common tumors (with a background prevalence rate of 2 %) will be misclassified as rare, and judged against the “wrong” significance thresholds. Given the difference in the significance thresholds between those used for rare and for common tumors, it is to be expected that this misclassification effect could have an appreciable liberalizing effect on the decision rules used. Furthermore, this liberalizing effect will be amplified by the fact that misclassification is positively associated with low p-values.10 This effect was noted, discussed, and even quantified (albeit for different decision rules and simulation scenarios than those used here) in Westfall and Soper (1998).
The probability of misclassification is dependent on both the background prevalence rate of the tumor and the number of animals in the control group. Since D2 has more than 100 animals in the control group, an experiment using this design will treat a particular tumor endpoint as rare if there is no more than one tumor bearing control animal; the other designs will consider an endpoint to be rare only if no tumor bearing control animals are found at all. The effects of this difference are seen in Fig. 12.2.
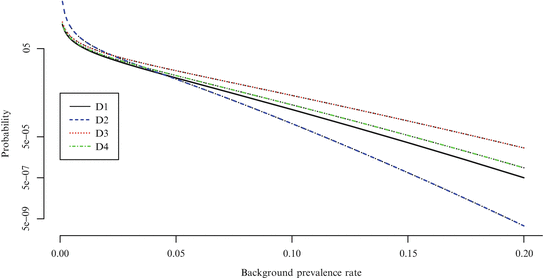

Fig. 12.2
Probability of classifying a tumor type as rare
Under more traditional circumstances, given an exact test procedure and a fixed set of significance standards, one would expect the false positive rate to increase asymptotically to the nominal level as the expected event count increased. However, given the misclassification effect in this context, we expect something different; for tumors with a 2 % background prevalence rate (and for those with a 5 % background rate in the simulation study in Sect. 12.2), the LFPR can be anticipated to converge to a value below the nominal significance level for rare tumors, but above the nominal significance level for common tumors. For tumors with a 10 % background prevalence rate, by contrast, we can expect the LFPR to be somewhat closer to the nominal value for common tumors.11
It is uncertain whether the differential effect of misclassification on the four designs should be viewed as intrinsic to the designs, or an additional, unequal source of noise. However, given the paucity of relevant historical control data (Rahman and Lin 2009), and that a two tiered decision rule is in use, there seems to be little alternative to this method for now.12 Accordingly, this is the most commonly used method for classifying tumors as rare or common, and we have elected to treat it as an intrinsic feature of the statistical design.
Nonetheless, it should also be remembered that statistical analysis is only one stage in the FDA review process, and that pharmacology and toxicology reviewers are free to exercise their professional prerogative and overturn the empirical determination. This is especially likely for the rarest and commonest tumors. More generally though, it is apparent that this misclassification effect must be taken into account when designing, conducting, and interpreting any simulations to evaluate carcinogenicity studies.
12.3.5 Power
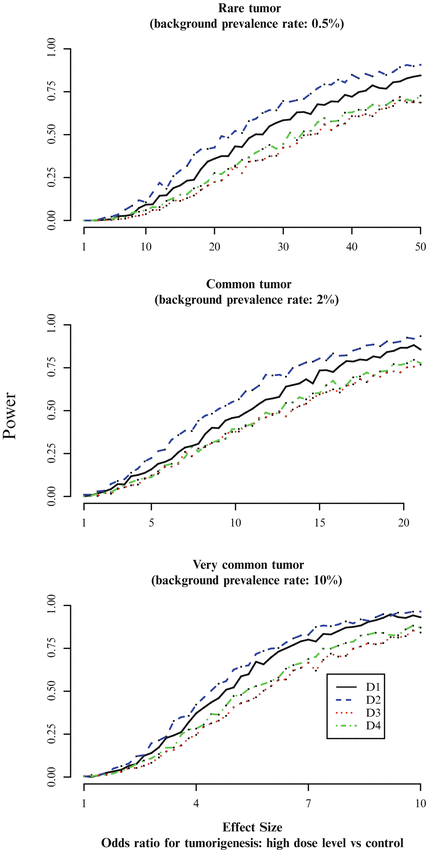
Designs D1 and D2 are clearly more powerful than D3 and D4. For very common tumors, there is little difference between the two, but for both rare and common tumors, design D2 appears to be appreciably more powerful than D1. For rare tumors and an effect size of 30 (corresponding to a risk difference (RD) between the control group and the high dose group of 12.6 %), D1 and D2 have approximately 60 and 70 % power respectively. For common tumors and an effect size of 10 ( RD=14.9%), D1 and D2 have approximately 45 and 55 % power respectively. More generally, Fig. 12.3 suggests that design D2 delivers about 10 % more power than D1 across a fairly wide range of scenarios of interest.
Since it uses the fewest animals, it is not surprising that D3 is the least powerful of the four designs. Direct comparison of D3 and D1 (which are similar except for the fact that D1 uses 30 % more animals in each group) shows the benefit in power that an increased sample size can bring.
That said, it is striking that the design D4, with 260 animals, is barely more powerful than D3. As we have seen from our comparison of D1 with D3, adding animals in such a way that the groups remain equal in size does increase the power of the design (absent any sawtooth effects). Furthermore, adding animals unequally to the groups can improve the power even more (see Jackson 2015). However, in the case of design D4, the extra animals (compared with D3) were not added with the goal of improving power. Indeed, the notion of optimality which D4 is intended to satisfy is quite different from our narrow goal of maximizing power while keeping the GFPR to approximately 2.5 % (Portier and Hoel 1983):
For our purposes, an optimal experimental design is a design that minimizes the mean-squared error of the maximum likelihood estimate of the virtually safe dose from the Armitage-Doll multistage model and maintains a high power for the detection of increased carcinogenic response.
In addition, the intended maintenance of “a high power for the detection of increased carcinogenic response” was predicated on a decision rule using the trend test alone, with a significance threshold of 0. 05—a much more liberal testing regime even than that recommended in US Food and Drug Administration—Center for Drug Evaluation and Research (2001), let alone than the more conservative joint test rule used here.
It is worth noting that the unbalanced approach of Design D4 is almost the anthesis of that proposed in Jackson (2015); in the latter, power is maximized by concentrating animals in the control and high dose groups, whereas in D4 they are concentrated in the intermediate groups.
12.3.6 False Positive Rate
12.3.6.1 The Local False Positive Rate
For each design, at least 250,000 simulations were conducted to estimate the rate at which the local null hypothesis is rejected when the tumor hazard is unchanged across dose groups. The resulting estimates of the LFPR (with 95 % confidence intervals) for each of the four designs and three tumor types (rare, common, and very common) are shown in Table 12.8.
Table 12.8
Local false positive rates (%) with 95 % confidence intervals
Background prevalence rate | ||||||
|---|---|---|---|---|---|---|
Design | 0. 5 % (rare) | 2 % (common) | 10 % (very common) | |||
D1 | 0.0024 | (0.0009,0.0052) | 0.2264 | (0.2078, 0.2450) | 0.3000 | (0.2786, 0.3214) |
D2 | 0.0424 | (0.0343,0.0505) | 0.5928 | (0.5627, 0.6229) | 0.3792 | (0.3551, 0.4033) |
D3 | 0.0012 | (0.0002,0.0035) | 0.1008 | (0.0884, 0.1132) | 0.4528 | (0.4265, 0.4791) |
D4 | 0.0011 | (0.0000,0.0024) | 0.1048 | (0.0926, 0.1169) | 0.2070 < div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

| |