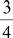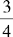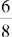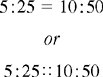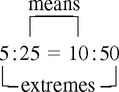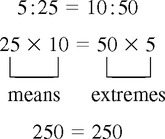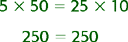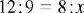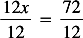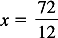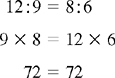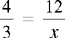Ratio and Proportion

Ratio and Proportion

After reviewing this chapter, you should be able to:

1. Define ratio and proportion

2. Define means and extremes

3. Calculate problems for a missing term (x) using ratio and proportion

Ratio and proportion is one logical method for calculating medications. It can be used to calculate all types of medication problems. Nurses use ratios to calculate and to check medication dosages. Some medications express the strength of the solution by using a ratio. Example: Epinephrine label may state 1:1,000. Ratios are used in hospitals to determine the client to nurse ratio. Example: If there are 28 clients and 4 nurses on a unit, the ratio of clients to nurses is 28:4 or “28 to 4” or 7:1. As with fractions, ratios should be stated in lowest terms. Like a fraction, which indicates the division of two numbers, a ratio indicates the division of two quantities. The use of ratio and proportion is a logical approach to calculating medication dosages.

RATIOS

A ratio is used to indicate a relationship between two numbers. These numbers are separated by a colon (:).

Example:

The colon indicates division; therefore a ratio is a fraction.

The numbers or terms of the ratio are the numerator and denominator. The numerator is always to the left of the colon, and the denominator is always to the right of the colon. Like fractions, ratios should be stated in lowest terms.

Example 1:

3:4 (3 is the numerator, 4 is the denominator, and the expression can be written as 34)

Example 2:

In a nursing class, if there are 25 male students and 75 female students, what is the ratio of male students to female students? 25 male students to 75 female students = 25 male students per 75 female students = 25/75 = 1/3. This is the same as a ratio of 25:75 or 1:3.

Ratio Measures: in Solutions

Some medications express the strength of the solution by using a ratio. Ratio measures are commonly seen in solutions. Ratios represent parts of medication per parts of solution, for example, 1:10,000 (this means 1 part medication to 10,000 parts solution).

Example 1:

A 1:5 solution contains 1 part medication in 5 parts solution.

Example 2:

A solution that is 1 part medication in 2 parts solution would be written as 1:2.

Ratio strengths are always expressed in lowest terms.

Tips for Clinical Practice

The more solution a medication is dissolved in, the less potent the strength becomes. For example, a ratio strength of 1:1,000 (1 part medication to 1,000 parts solution) is more potent than a ratio strength of 1:10,000 (1 part medication in 10,000 parts solution). A misunderstanding of these numbers and what they represent can have serious consequences.

PROPORTIONS

A proportion is an equation of two ratios of equal value. The terms of the first ratio have a relationship to the terms of the second ratio. A proportion can be written in any of the following formats:

Example 1:

3:4 = 6:8 (separated with an equals sign)

Example 2:

3:4 = 6:8 (separated with a double colon)

Example 3:

34 = 68 (written as a fraction)

Read as follows: 3 is to 4 equals 6 is to 8; 3 is to 4 as 6 is to 8; or, as a fraction, three fourths equals six eighths.

Proving that ratios are equal and that the proportion is true can be done mathematically.

Example:

5:25=10:50or5:25::10:50

The terms in a proportion are called the means and extremes. Confusion of these terms can result in an incorrect answer. To avoid confusion of terms in proportions, remember m for the middle terms (means) and e for the end terms (extremes) of the proportion. Let’s refer to our example to identify these terms.

The extremes are the outer or end numbers (previous example: 5, 50), and the means are the inner or middle numbers (previous example: 25, 10).

Example:

In a proportion the product of the means equals the product of the extremes. To find the product of the means and extremes you multiply.

In other words, the answers obtained when you multiply the means and extremes are equal.

Example:

The product of the means, 250, equals the product of the extremes, 250, proving the ratios are equal and the proportion is true.

To verify that the two ratios in a proportion are equal and that the proportion is true, multiply the numerator of each ratio by its opposite denominator. The products should be equal. The numerator of the first fraction and the denominator of the second fraction are the extremes. The numerator of the second fraction and the denominator of the first fraction are the means.

Example:

5:25=10:50525=1050(proportion written as a fraction)

When stated as a fraction, the proportion is solved by cross multiplication.

5×50=25×10250=250

SOLVING FOR x IN RATIO AND PROPORTION

Because the product of the means always equals the product of the extremes, if three numbers of the two ratios are known, the fourth number can be found. The unknown quantity may be any of the four terms. In a proportion problem, the unknown quantity is represented by x. After multiplying the means and extremes, the unknown x is usually placed on the left side of the equation. Begin with the product containing the x that will result in the x being isolated on the left and the answer on the right.

Example:

Steps:

12x = 72	1. Multiply the extremes and then the means. (This results in x being placed on the left side of the equation.)
12x12=7212	2. Divide both sides of the equation by the number preceding the x, in this instance 12, without changing the relationship. The number used for division should always be the number preceding the unknown (x), so that when this step is completed, the unknown (x) will stand alone on the left side of the equation.
x=7212
x = 6

Proof:

Place the answer obtained for x in the equation, and multiply to be certain that the product of the means equals the product of the extremes.

12:9=8:69×8=12×672=72

Solving for x with a proportion in a fraction format can be done by cross multiplication to determine the value of x.

Example:

Steps:

1. Cross multiply to obtain the product of the means and extremes.

Only gold members can continue reading. Log In or Register to continue

Related

Stay updated, free articles. Join our Telegram channel

Tags: Calculate with Confidence

Feb 11, 2017 | Posted by admin in PHARMACY | Comments Off

Full access? Get Clinical Tree

Get Clinical Tree app for offline access

Get Clinical Tree app for offline access