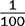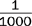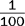Ratio and Proportion
Introduction
Ratio and proportion is an easy, provable method of drug dose calculation. The setup of problems is logical and systematic. Answers can be proven if the setup is correct.
Ratio
A ratio indicates the relationship of one quantity to another. It indicates division and may be expressed in fraction form.
Example
⅓ may be expressed as the ratio 1:3.
Express the following ratios as fractions reduced to lowest terms.
Proportion
A proportion shows the relationship between two equal ratios. A proportion may be expressed as 3 : 5 :: 6 : 10 or 3 : 5 = 6 : 10.
To solve the ratio and proportion problems, do the following:
Example
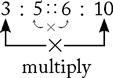
Multiply the two inside numbers: 5 × 6 = 30.
Multiply the two outside numbers: 3 × 10 = 30.
Solving Proportion Problems When One of the Numbers Is Unknown, or x
Example
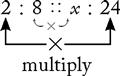
Multiply the two inside numbers (means).
8 × x = 8x
Multiply the two outside numbers (extremes).
2 × 24 = 48
Move the x product to the left side of the equation. It will now look like this:
8x = 48
Now you must get x to stand alone.
RULE
To solve for the value of x, divide both sides of the equation by the number next to x. Those numbers will cancel each other. The result will be that x will stand alone.
What you do to one side of the equation, you must do to the other to keep the sides equal.
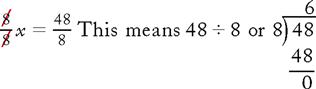
Example
x = 6
How do you know your answer is correct?
RULE
To check your answer, substitute the answer for the x in the problem, multiply the inside numbers together, and then multiply the outside numbers together. The products should be equal.
Another way to view this example is:
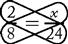
Cross-multiplication solves this equation: 8x = 48 x = 6
Example
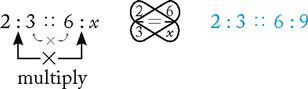
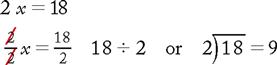
remember
Divide both sides by the number next to x.
Multiply the two inside numbers, multiply the two outside numbers, then move the x product to the left side of the equation. Solve for x.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree