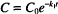This expression states that the rate is proportional to the drug concentration (C) raised to some power, P. The value of P identifies the order of the equation. Its origin in the case of relatively simple reactions is the number of molecules of a given reactant that participate in the reaction. In a practical sense, the assignment of order is empirical, based on the way a system behaves rather than fundamental mechanisms.

Thus a first-order rate expression has the form

while a second order equation would be

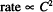
Write the form for a zero-order rate expression.

Solution. Rate ∞ C⁰

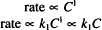
The subscript 1 is used with k to emphasize that this equation is first-order. Write the equation (including a proportionality constant, k₀) to describe the rate of a zero-order process.

Solution. Rate = k₀C⁰ = k₀ (any number raised to the zero power has a value of one)

Let us start with the zero-order rate equation:

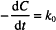
Integration leads to the following solution:

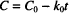
C₀ is the initial concentration. C and C₀ are in the same units, which might, for example, be g/100 mL or mg/mL or mol/L, while t can be any valid time units (i.e., seconds, minutes, hours, days, etc.). The product of k₀ and t must have the same units as C₀, to allow one term in the equation to be subtracted from the other. k₀ therefore has the units of concentration divided by time. If C₀ is in mg/mL and t is in hours, the units of k₀ are mg/mL/h.

Another way of writing this is mg mL⁻¹h⁻¹.

What units would be used for k₀ if drug concentration is expressed in moles/liter and time in days?

Solution. mol L⁻¹ day⁻¹

As t changes from zero (the time at which the solution is prepared), drug concentration drops from C₀; the equation allows us to calculate the value of C corresponding to any value of t. As you can see from the equation, the concentration of drug remaining in solution decreases over time in a linear fashion. This is the defining characteristic of a zero-order relationship.

If a plot of drug concentration vs. time is a straight line, what is the order of the process?

Solution. Zero is correct. Linear degradation rate is synonymous with a zero-order rate law.

Solution. 2.42 mg/mL (or 0.242%)

CALCULATIONS

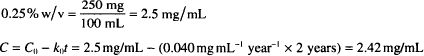
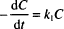
This expression should look familiar to you. It has the same form as the equation for radioactive decay. All of the mathematical properties that we studied in Chapter 13 apply here.

The three variations of the integrated equation for first-order degradation are:

(1)

(2)

(3)

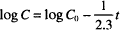
Recall that “ln” refers to the natural logarithm (to the base e), while “log” refers to the logarithm to the base 10. The other symbols were defined earlier. The units of k₁ are reciprocal time s⁻¹, h⁻¹, days⁻¹, and so on. Dividing both sides in Eq. (1) by C₀ leads to

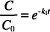
The left-hand side of the equation is now a ratio of the concentration values. This ratio represents the fraction of the original concentration remaining after degradation has proceeded for a given period of time, t. Over any time period chosen, the ratio C/C₀ is constant regardless of what the starting concentration, C₀, was. Over that same time period, the fraction of unchanged drug remaining will always be the same.

We have two flasks containing different concentrations of the same drug. The concentration in flask A is 0.11 molar; the concentration in flask B is 0.35 molar. If the degradation process is first-order and both flasks are stored at the same temperature for 6 months, in which will the highest percentage of initial drug remain?

Flask A

Flask B

They will be the same

Solution. They will each have the same percentage of initial concentration because the degradation process is first-order.

Solution. 1.33 mg/mL

CALCULATION

The concentration remaining at the end of 3 months is 1.5 mg/mL × 0.94 = 1.41 mg/mL. 1.41 mg/mL is the starting concentration for the second 3-month period. At the end of that time, the concentration remaining should be 1.41 mg/mL × 0.94 = 1.33 mg/mL.

Solution. 0.082 molar

CALCULATION

The drug retains 80% of its initial concentration in each 25-day period. The concentration remaining after three such periods is 0.16 molar × 0.8 × 0.8 × 0.8 = 0.082 molar.

One standard way of expressing this idea is in terms of a half-life or half-time for degradation. This is the time required to bring the concentration down to 50% of its initial value. The symbol used is t_1/2, t_0.5, or t_50%.

The second fraction of great interest, t₀.9, relates to drug stability in manufactured products. This is the time required for the concentration to drop to 90% of its original value. For most products, 90% of original content is the point at which the end of the shelf life is reached. Thus, t_0.9 is equivalent to the shelf life.

We can obtain both of these values by making the appropriate substitution in any of the rate equations. C = 0.5 C₀ when t = t_0.5 and C = 0.9 C₀ when t = t_0.9. When we do so, the following results are obtained:

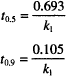
Notice that neither equation contains a concentration term; t_0.5 and t_0.9 for a first-order process are independent of the starting concentration.

A solution containing 0.636 g/100 mL of drug is stored in a closed container at 20 °C. It degrades by a first-order process and the rate constant at this temperature is 0.00215 day⁻¹.

Calculate the time required for the concentration to drop to

Stay updated, free articles. Join our Telegram channel

Join