Although SMILES strings have their limitations they have proven to be an effective representation of a compound.
To create many types of models, some numeric representation of the structure is required. There are a wide variety of such chemical descriptors (Leach and Gillet 2007). Some examples:
Simple count of specific atoms or bonds (e.g. the number of covalent bonds or the number of carbons) are commonly used.
Fingerprint descriptors are binary indicators for specific sub-structures or fragments. There are potentially millions of possible fingerprint descriptors. In many data sets, fingerprint descriptors tend to be very sparse, meaning that they are mostly zero across different compounds.
There are numerous descriptors that are represented by continuous values such as molecular weight, surface area, volume and positive charge. Other, more esoteric descriptors exist such as the flexibility index of the longest chain in the molecule.
Some descriptors used are estimated based on pre-defined models. For example, lipophilicity (or “greasiness”) is an important property. The most common representations of this property is logP, where P is the partition coefficient that measures the ratio in concentrations between water and octanol. For example, polar compounds will tend to concentrate in water and yield lower logP value. There are assay systems that can measure logP. However, when used as inputs into QSAR models, this descriptor is usually quantified by an existing model. See Machatha and Yalkowsky (2005) for examples.
For continuous descriptors, it is common to observe high degrees of between-predictor correlations. This can occur for several reasons. First, there are many different methods for calculating certain descriptors. For example, different versions of surface area include or exclude some atoms (e.g., nitrogen or oxygen) which can lead to extremely high correlations. Secondly, there are many different descriptors that quantify the same underlying characteristic of the molecule. The number of bonds is likely correlated with the number of atoms in the molecule and these in-turn have a relationship to the size and weight of a compound. This characteristic of molecular descriptors can induce severe multicollinearity (Myers 1990) in the data which can have a significant effect on some statistical models.
For example, using the data from Karthikeyan et al. (2005) where 4173 compounds were used to predict the melting point of a molecule. Using a set of 202 molecular descriptors, the average absolute correlation between pairs of descriptors was 0.26. However, a principal component analysis (Abdi and Williams 2010) of the data indicated that the first three components of the data accounted for 96 %, 3.2 % and 0.4 % of the variance, respectively. This implies that the vast majority of the descriptors used in the analysis were capturing the same (linear) information and are redundant.
6.3 Structure Based Models
One simplistic model that relates structure to potency was created by Free and Wilson (1964). In some situations, portions of a molecule can be treated as a single unit that can be substituted in different ways. An R group is a place holder for a structure that can be attached to an end of a molecule (i.e. a side chain). A set of compounds might be represented as one or more core molecules that are constant along with several possible R groups. For example, Free and Wilson describe a single core molecule with two locations for substitutions (i.e. R 1 and R 2). In their data, the possible values of R 1 were either H or CH3 while R 2 could have been N(CH3)2 or N(C2H5)2. Based on this, there are four possible molecules that could be represented in this way. In practice, the number of “levels” in the R groups is typically large.
The Free-Wilson model is a simple ANOVA model that is additive in the R groups. A possible design matrix for these data might be
Molecule | Intercept | R 1 | R 2 |
|---|---|---|---|
Core + H + N(CH3)2 | 1 | 0 | 0 |
Core + CH3 + N(CH3)2 | 1 | 1 | 0 |
Core + H + N(C2H5)2 | 1 | 0 | 1 |
Core + CH3 + N(C2H5)2 | 1 | 1 | 1 |
where R 1 is an indicator for compounds that contain CH3 and R 2 is an indicator for N(C2H5)2. To understand the relationship between potency and molecular structure, a linear model could be used:
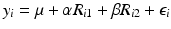where y i are the potency values for compound i, μ is the grand mean and the ε i are the model residuals that might be assumed to be normally distributed under the standard assumptions for ordinary linear regression. The utility of this model is twofold. First, it may be possible to get accurate potency predictions for new molecules whose combinations of R groups have not been synthesized or assayed. This depends on how effective the additive structure of the Free-Wilson model is at describing the data. The second use of the model is for the chemist to understand how changes in structure might increase or decrease potency for the current set of molecules currently under consideration. In practice, a Free-Wilson model would usually have effects for different R groups that have many different substructures (instead of only two distinct values for R 1 and R 2 shown above). This is case, there will be many regression parameter estimates that the chemist can use to understand the effect of adding each R-group structure.
The stereotypical QSAR model tends to be more sophisticated and uses a wider variety of compounds/descriptors and has a stronger focus on prediction. Instead of modeling specific R groups, they might include more general predictors such as atom counts or descriptors of size and charge. More general descriptors (i.e. not based on R groups) would allow more direct prediction of new molecules whereas the Free-Wilson model is confined to predictor compounds within the range of the R groups observed in the data set.
QSAR models can generally be grouped into classification or regression models. While these are imperfect labels, we use classification to denote the prediction of a discrete outcome (e.g. toxic or non-toxic) while regression is used to denote models that predict some continuous value (e.g. EC 50, solubility, etc.). The type of predictive model used can vary greatly. In some cases, simple linear regression models are used while others might use more complex machine learning models to fit the data. Most statistical prediction models can be grouped in terms of their bias and variance (Friedman 1997). Models with low variance tend of have high bias. Examples of these models are linear regression and linear discriminant analysis. They are numerically stable models (i.e. low variance) that lack the ability to model complex trends in the data (i.e. high bias). In the other extreme are models that are very flexible and can fit to most any pattern in the data (hence low bias) but may the propensity to over-fit the model to patterns that may or may not generalize to new data. These models also tend to be unstable (i.e. high variance), meaning that changes to the data can have considerable effects on the model. An example of one such model is the artificial neural network (Bishop 2007). The choice between these two class of models tends to depend on the QSAR modeler and their prior education and experiences. For descriptions and discussions of different types of predictive models, see Hastie et al. (2008) or Kuhn and Johnson (2013).
An an example, Kauffman and Jurs (2001) use predictive models to estimate the potency of cyclooxygenase-2 (COX-2) inhibitors. They modeled the log(EC 50) values of compounds that were created by four chemical series. Their focus was on topological descriptors, which are derived by converting the SMILES string to a 2D network diagram of atoms then calculating summary metrics on this graph. These descriptors convey information related to the size and shape of the molecule (among other characteristics). Their models used such 74 descriptors. They evaluated two different models to predict the log(EC 50) values: ordinary linear regression and artificial neural networks.
Given an initial pool of 273 compound, they split the data into three partitions:
a training set of 220 compounds used to estimate (or “train”) the model parameters
a validation set of 26 compounds used primarily to tune the neural network meta-parameters and
a test set of 27 compounds that are utilized to obtain an unbiased estimate of model performance.
The test set root mean square error value for the ordinary linear regression was 0.655 log units and the neural networks was able to obtain a value of 0.625 log units. There was no appreciable difference between the neural network and linear regression models that were above and beyond the experimental variation. Given a new set of compound structures, the potency can be predicted and these values can be used to rank or prioritize which compounds should be synthesized or given more attention.
Note that the model building process has an emphasis on empirical validation using a set of samples specifically reserved for this purpose. While is an extremely important characteristic of predictive modeling in general, there is an added emphasis using QSAR modeling. This is a stark contrast to most classical statistical methods where statistical hypothesis tests (e.g. lack of fit) are calculated from the training set statics and used to validate the model. The emphasis on a separate test set of samples is not often taught in most regression modeling textbooks. Also, for many classic statistical models, the appropriateness of the model is might be judged by a statistical criterion that is not related to model accuracy (e.g. the binomial likelihood). Here, the focus is on creating the most accurate model rather than the most statistically legitimate model. One would hope that a statistically sound model would be the most accurate but this is not always the case. Friedman (2001) describes an example where “[…] degrading the likelihood by overfitting actually improves misclassification error rates. Although perhaps counterintuitive, this is not a contradiction; likelihood and error rate measure different aspects of fit quality.”
There are abundant examples of QSAR models in journals such as the Journal of Chemical Information and Modeling, the Journal of Cheminformatics, the Journal of Chemometrics, Molecular Informatics and Chemometrics and Intelligent Laboratory Systems. Many of the methodologies developed in these sources have applications outside of QSAR modeling. Additionally, it is very common for articles on these journals to contain the sample data in supplementary files, which enables the reader to reproduce and extend the techniques discussed in the manuscripts.
6.4 Non-structure Models
The intent of QSAR models is to use existing data to predict important characteristics to increase the efficiency and effectiveness of drug design. While structural descriptors are often used, there are occasions where assay data exists that can be used instead.
For example, compound “de-risking” is the process of understanding potential toxicological liabilities based on existing data. Maglich et al. (2014) created models to assess the potential for reproductive toxicity in males by measuring a compound’s effect on steroidogenic pathways. They used 83 compounds known to be reproductive toxicants and 79 “clean” compounds and ran assays to measure a number hormone levels as well as the RNA expression of several important genes. These models can then be used to screen new molecules for reproductive toxicity issues.
In another safety-related model, Sedykh et al. (2010) use the biological in vitro assay outcomes from dose-response curves as predictors of in vivo toxicity. Their analysis showed that a model using the assay data and molecular descriptors improved the predictive power of the model.
6.5 Other Aspects of QSAR Models
The field of QSAR modeling has matured to the point where the current literature has been exploring the more subtle issues related to predictive modeling.
6.5.1 Applicability Domains and Model Confidence
One key consideration for project teams is choosing between global and local models. Local models are built using the compounds that have been generated to-date for the current project. Global models are built using a much larger, broader set of compounds. In some cases, there may be global and local QSAR models for the same characteristic. In theory, global models should be better than local models since they have typically use more diverse data to train the models. However, in practice, local models tend to do better since they are built with the most relevant data. The earlier example from Kauffman and Jurs (2001) was a local model that used compounds from four chemical series (as opposed to a highly diverse compound set).
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
