Factors that contribute to driving forces include gravitation, particle mass, the angle of inclination of the powder and any applied load, while factors that contribute to drag forces include forces of adhesion or cohesion, electrostatic forces, water bridges and mechanical interlocking. Good flow would mean the powder would move under gravity, without the need for any additional excipients. In quantitative terms, flow means that the powder mass deforms plastically in response to an applied load (or stress).
In general, particle size greatly influences flow properties and is the easiest variable to change during processing. Fine powders, with high surface area-to-mass ratios, tend to be affected more by the force of cohesion. Coarse particles tend to be affected more by gravitational forces. As a general rule, particles larger than 250 μm are usually free flowing, but cohesive forces start to predominate when the particle size reduces to 100 μm or less. When the particle size is as small as 10 μm, powders are usually very cohesive.
The density of a powder is defined by the ratio of its mass to volume; however, unlike pure solids, powders consist of solid particles with air (or void) spaces between them. Thus, while the individual particles have a true density, the measured density of the powder will be smaller, as a result of the void spaces. The term bulk density is used to describe the density of the powder and its value must be smaller than the true density of the particles. It follows that bulk density may vary. For instance, if the particle size distribution of a sample decreases, the ratio of void space to particles will also decrease, increasing the bulk density. In this case, bulk density must be defined for a powder with a certain particle size distribution. Further, if a powder is poured into a container, it is likely that initially the particles are at their least ordered (i.e. the ratio of void space to particles will be at its highest and the bulk density at its lowest). This is defined as the ‘poured’ or ‘fluff’ bulk density. Tapping the sample will result in reduction of the bulk volume as the particles reorder themselves (termed consolidation). The ratio of void space to particles will be at its lowest and the bulk density at its highest. This is called the ‘tapped’ or ‘final’ bulk density.
Determination of fluff and tapped bulk density indicates the degree to which a powder will consolidate under gravity. If an additional load is applied vertically to the powder, further consolidation will occur. For a consolidated powder to flow, the gravitational force must be sufficient to overcome the forces of consolidation and cause plastic deformation.
A number of indices have been developed to relate the degree of consolidation to powder flow properties. The two most commonly used are those of Carr (1965) and Hausner (1967). In addition, the relationships between stresses and powder flow can be visualised with a Mohr diagram.
- Whether a powder flows or not depends on the balance between driving forces and drag forces.
- Drag forces are influenced by particle size and shape.
- Particles greater than 250 μm tend to be free flowing, while those below 100 μm tend to be cohesive.
- Particles have a true density, but the density of the bulk powder will be smaller, because of void spaces.
- A freshly poured powder will have a lower bulk (fluff) density than a consolidated powder (tapped density).
11.2.1 Carr’s index
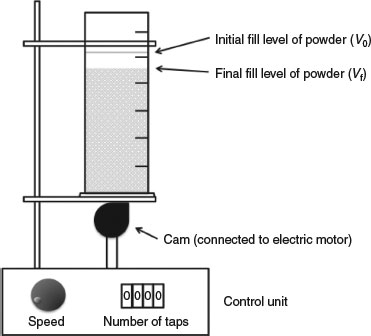
Carr (1965) developed a simple test using a jolting volumeter. This apparatus consists of a measuring cylinder located vertically in a frame with a cam below it; as the cam rotates, the measuring cylinder is jolted up and down, simulating tapping. The speed of rotation of the cam and the number of taps are controlled by an electronic interface and motor. The number and force of each tap are thus precisely controlled. A typical experimental apparatus is shown in Figure 11.1.
The powder is sieved initially, rather than poured, into the cylinder so that it is at its maximum porosity and has not been partially compressed by the filling process. Then all that is necessary is to measure the volume of a given weight of a bulk powder before tapping to obtain the fluff density and again after vertically jolting the cylinder to give the tapped density.
When large quantities of material are available, a 100 mL measuring cylinder is employed. Clearly, during early development phases much less drug candidate may be available, so the equipment may be modified with a smaller measuring cylinder. One option would be to mount the small cylinder through a rubber bung and position it in the neck of the larger cylinder.
The initial volume is recorded and called V0. Then the contents are jolted and the volume of the powder recorded after 2, 4, 6, 8, 10, 12, 15, 20, 30 and finally 50 taps (Vf). Weighing the cylinder full and again empty will give the weight of powder (W). From this, the fluff density (g mL−1) can be calculated from W divided by V0 and the tapped density from W divided by Vf.
Carr quantified the degree of ‘compressibility’ as
(11.2)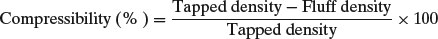
The relationship between Carr’s compressibility index and the probable flow properties of a powder mass is shown in Table 11.1.
Table 11.1 Relationships between Carr’s compressibility index, Hausner ratio and powder flow.
| Carr’s compressibility index (%) | Hausner ratio | Description of flow |
| <10 | 1.00–1.11 | Excellent |
| 11–15 | 1.12–1.18 | Good |
| 16–20 | 1.19–1.25 | Fair |
| 21–25 | 1.26–1.34 | Passable |
| 26–31 | 1.35–1.45 | Poor |
| 32–39 | 1.46–1.59 | Very poor |
| >40 | >1.60 | Very, very poor |
11.2.2 Hausner ratio
A similar index was defined by Hausner (1967). The Hausner ratio is defined as
(11.3)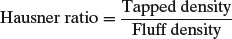
The relationship between the Hausner ratio and powder flow is given in Table 11.1. Because both Carr’s and Hausner’s ratios are one-point determinations, calculated from the initial and final volumes of the powder, they do not indicate the ease and speed with which consolidation occurs. Some materials might have quite a high index (suggestive of poor powder flow) but in fact compress rapidly. This is very useful for uniform die filling on tablet machines when the powder may flow into the die close to its minimum density and then quickly compresses to maximum density prior to consolidation. An empirical linear relationship exists between the percentage bulk density and the log of the number of taps. Nonlinearity occurs up to 2 taps and then after 30 taps when the bed compresses more slowly. Between these points the relationship should be linear, the slope being a measure of the speed of compression. The value is useful for assessing powders or blends of powders of similar indices, the beneficial effects of glidants and/or the design of capsule formulations.
11.2.3 Angle of repose
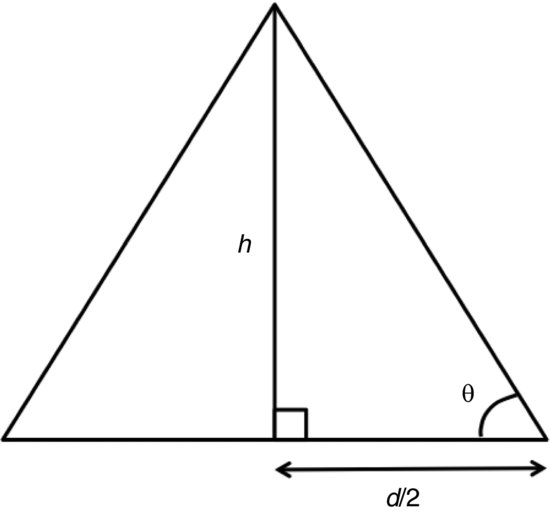
If a mass of powder is poured on to a flat surface it will form a cone with a characteristic angle to the horizontal surface. Assuming the powder is free flowing, the angle will be small and a shallow cone will be formed. Conversely, where the powder exhibits poor flow the angle will be high. The angle, known as the angle of repose (θ), can therefore be used to predict powder flow even when only a small amount of material is available.
Experimentally, a mass of powder is placed in a funnel (the base of which is blocked with a rubber bung) over a metal disc. The bung is removed and the powder falls on to the disc, forming a heap. The diameter of the base of the heap is known, and a constant, because the size of the metal disc is known.
If the height (h) and diameter (D) of the cone are determined, θ can be calculated (Figure 11.2):
(11.4)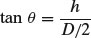
Measurements of θ are notoriously variable, but it is still possible to relate θ to flow, as shown in Table 11.2. It is most important to ensure that the top of the cone is not rounded by powder falling and impacting on the top of the cone.
Table 11.2 Relationship between angle of repose and powder flow.
| Angle of repose (θ) | Description of flow |
| <25 | Excellent |
| 25–30 | Very Good |
| 31–35 | Good |
| 36–40 | Fair |
| 41–45 | Passable but flow aid might be needed |
| 46–55 | Poor – agitation or vibration needed |
| >56 | Very poor |
Study question 11.1 Can you see the problem of inaccurate measurement of θ generated by rounding the top of the cone? Can you suggest a test method that would not deform the cone?
Study question 11.2 Can you suggest how you might adapt existing or standard angle of repose determinations when only a small weight of powder is available?
In general, powder behaviour can be split into three categories:
- Low Carr’s index, low angle of repose. Flow is good so no future problems are likely.
- Mid-range values for Carr’s index and angle of repose. Flow can probably be improved with additives.
- High values of Carr’s index and angle of repose. Flow is extremely poor and cannot be improved sufficiently with the use of additives.
Study question 11.3 Can you suggest which additives may be useful in improving the flow of powders with mid-range values for Carr’s index? What might be done for powders with high Carr’s index values?
Study question 11.4 Explain how the angle of repose and powder flow are related in terms of interparticulate cohesion.
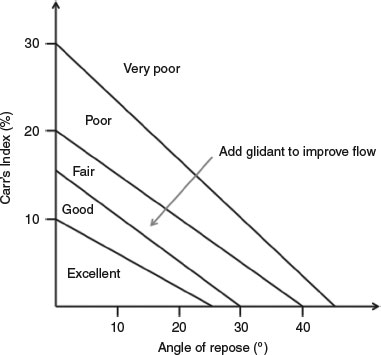
Figure 11.3 summarises the interrelationship between Carr’s compressibility index, the angle of repose and flowability of a powder.
Figure 11.3 Relationship between Carr’s index and angle of repose and the consequence for powder flowability.
- Carr’s index and the Hausner ratio are two methods used to define the compressibility of a powder and either can be measured with a tapping volumeter.
- Angle of repose is derived from a powder heap – lower angles imply better flow.
- The correlation of Carr’s index with angle of repose gives a good indication of bulk powder flow properties.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree