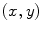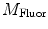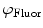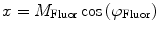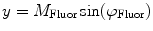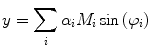, Kai Wen Teng1 and Robert M. Clegg1, 2
(1)
Center of Biophysics and Computational Biology, University of Illinois at Urbana-Champaign, Urbana, IL, USA
(2)
Loomis Laboratory of Physics, Department of Physics, University of Illinois at Urbana-Champaign, Urbana, IL, USA
Abstract
Measuring changes in a molecule’s fluorescence emission is a common technique to study complex biological systems such as cells and tissues. Although the steady-state fluorescence intensity is frequently used, measuring the average amount of time that a molecule spends in the excited state (the fluorescence lifetime) reveals more detailed information about its local environment. The lifetime is measured in the time domain by detecting directly the decay of fluorescence following excitation by short pulse of light. The lifetime can also be measured in the frequency domain by recording the phase and amplitude of oscillation in the emitted fluorescence of the sample in response to repetitively modulated excitation light. In either the time or frequency domain, the analysis of data to extract lifetimes can be computationally intensive. For example, a variety of iterative fitting algorithms already exist to determine lifetimes from samples that contain multiple fluorescing species. However, recently a method of analysis referred to as the polar plot (or phasor plot) is a graphical tool that projects the time-dependent features of the sample’s fluorescence in either the time or frequency domain into the Cartesian plane to characterize the sample’s lifetime. The coordinate transformations of the polar plot require only the raw data, and hence, there are no uncertainties from extensive corrections or time-consuming fitting in this analysis. In this chapter, the history and mathematical background of the polar plot will be presented along with examples that highlight how it can be used in both cuvette-based and imaging applications.
Key words
Polar plotPhasor plotFluorescence lifetimeFrequency domain1 Introduction and History of the Polar Plot
The polar plot arose as a convenient method of analysis to study the response of systems such as electric impedance [1, 2], dielectric relaxation [3], fluorescence [4–7], and relaxation kinetics [8]. The signals of these systems decay exponentially (relax) in response to a sudden small external stimulus. For example, in the case of chemical relaxation kinetics, the measured emission of a fluorescence probe, which is thermodynamically coupled to a chemical reaction of interest, will decay exponentially in response to a sudden change in pressure or temperature of the system. Instead of reconstructing the exponential relaxations in the time domain, it is often more convenient to subject the system to repetitive perturbations, and examine the signals in the frequency domain (as sets of sine and cosine functions; see below). Both methods yield equivalent information concerning the underlying physical parameters. The polar plot simplifies the analysis of these types of measured signals by displaying the measured data graphically on the Cartesian plane.
Any repetitive signal can be decomposed into a sum of sine and cosine functions oscillating at a set of frequencies by Fourier series analysis [9, 10]. The coefficients that weight the sine and cosine functions at each frequency indicate the contribution that the specific frequency has to the original signal. These coefficients, which can span a wide range of frequencies depending on the waveform of the repetitive signal, are referred to as the signal’s frequency response. When summed over all frequencies and combined with a DC (or steady-state) term (long time average), the original signal can be reconstructed in its entirety. At each frequency, a particular amplitude of oscillation and phase delay characterize the system.
When studying relaxations in the frequency domain, the amplitude of oscillation and phase delay are dependent on both the repetitive frequency and the decay constants of the different components contributing to the relaxation. (See the later section discussing the measurement of lifetimes for derivations related to the amplitude of oscillation (modulation ratio) and phase delay to fluorescence lifetime measurements.) The polar plot applies a coordinate transformation to translate the modulation ratio and phase delay information into a polar vector on the Cartesian plane. All relaxations described by a single exponential decay will reside on a semicircle centered at (0.5, 0) with a radius of 0.5. Relaxations with multiple decaying components will be projected inside the semicircle. The relative contribution of independently decaying components to a measured decay can be assessed by simple vector addition in this representation. As a result, simply by observing changes in the position of a vector on the polar plot, quantitative information can be extracted to describe the relaxations of various systems.
The application of polar plots to study the lifetimes of fluorescent molecules (fluorescent relaxations) began in the early 1980s [6]. At that time, measuring lifetimes with large sets of repetitive frequencies was beginning to be used in order to examine the contribution of multiple distinct decaying components in cuvette-based fluorescence measurements [11–13]. The polar plot was used to verify the relationship between decay constants derived from the modulation ratio and phase delay for samples with multicomponent decays. When measuring lifetimes in images became more widely available, the simple graphical presentation and computational ease of the polar plot shortened data acquisition and analysis times and made the interpretations of complex systems more transparent. In parallel, three labs introduced the polar plot for such applications: the AB plot [4], polar plot [5], and phasor plot [7]. Currently, this graphical representation of fluorescence lifetimes is standard in most software packages for the acquisition and analysis of lifetime measurements.
In this chapter, we describe the basic steps necessary to generate a polar plot and extract physical information about a sample using the polar coordinate. The fundamentals of the polar plot can be equivalently applied to data collected from either cuvette-based measurements or to images taken with FLIM (fluorescence lifetime-resolved imaging microscopy). Specific examples from a variety of chemical and biological systems are also given to demonstrate the usefulness and graphical ease of the polar plot.
2 Methods
2.1 Fundamental Fluorescence Response
When a fluorescent molecule (fluorophore) absorbs light, fluorescence is observed as the excited fluorophore loses energy by the emission of a photon and returns to the ground state (de-excitation). The lifetime of the fluorophore is the average amount of time that the fluorophore spends in the excited state. If more avenues of de-excitation are available other than fluorescence, such as energy transfer, the fluorophore leaves the excited state more rapidly resulting in a shorter lifetime. The process of depleting the excited state can be described with first order rate kinetics where each pathway of de-excitation contributes a rate specific to its probability of occurring. Therefore, the probability that a fluorophore will remain in the excited state following a brief excitation decays exponentially in time [14–17].
Experimentally, the lifetime can be measured directly by exciting the molecule with a very brief (with respect to the lifetime) pulse of light and recording the fluorescent decay. The measured intensity at any point along the decay is proportional to the number of molecules remaining in the excited state at that time. The general equation for the fluorescent decay of a sample containing a set of fluorophores with different lifetimes is written in Eq. 1,
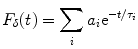
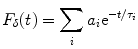
(1)
In Eq. 1, the factor 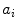 is proportional to the normalized concentration (species fraction) of fluorophore i with lifetime
is proportional to the normalized concentration (species fraction) of fluorophore i with lifetime 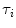 .
.
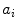 is proportional to the normalized concentration (species fraction) of fluorophore i with lifetime
is proportional to the normalized concentration (species fraction) of fluorophore i with lifetime 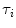 .
.2.2 Frequency Response
Measuring a sample’s lifetime in the frequency domain requires an excitation light that has its intensity repetitively modulated. Any repetitive waveform, including a pulsed excitation source, can be used to modulate the intensity of the exciting light to measure lifetimes in the frequency domain. This is because any sinusoidal constituent of a Fourier expansion of a repetitively intensity-modulated excitation source can be analyzed independently as a purely sinusoidal waveform exciting the fluorescence. It is also possible to transform data taken in the time domain to the frequency domain, such that a polar plot-based analysis can be applied. Thus, by analyzing the results from measurements taken either in the frequency domain or in the time domain, the polar plot can be constructed to graphically examine the frequency response of a fluorescing system.
In the frequency domain, the fluorescence from the sample is excited by a repetitively intensity-modulated source. The sample’s measured fluorescence 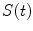 is analyzed to extract the average fluorescence, phase delay, and amplitude of oscillation (modulation ratio); from these parameters, a polar plot is constructed. If the fluorescence response to a repetitively intensity-modulated exciting light is defined over a definite period of repetition
is analyzed to extract the average fluorescence, phase delay, and amplitude of oscillation (modulation ratio); from these parameters, a polar plot is constructed. If the fluorescence response to a repetitively intensity-modulated exciting light is defined over a definite period of repetition 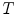 , a Fourier series analysis expands the measured repetitive fluorescent signal into a basis set of sine and cosine functions oscillating at a set of modulation frequencies
, a Fourier series analysis expands the measured repetitive fluorescent signal into a basis set of sine and cosine functions oscillating at a set of modulation frequencies 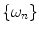 [9, 10],
[9, 10], 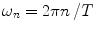 . The contribution of a specific repetitive frequency to the measured fluorescence (referred to as
. The contribution of a specific repetitive frequency to the measured fluorescence (referred to as 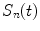 ) is defined by the coefficients
) is defined by the coefficients 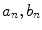 weighting the sine and cosine basis functions at each frequency
weighting the sine and cosine basis functions at each frequency 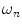 as shown in Eq. 2:
as shown in Eq. 2:
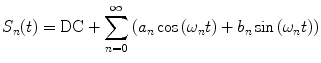
where 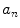 and
and 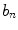 are defined in Eqs. 3 and 4.
are defined in Eqs. 3 and 4.
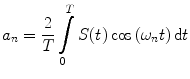
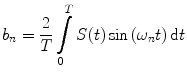
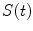 is analyzed to extract the average fluorescence, phase delay, and amplitude of oscillation (modulation ratio); from these parameters, a polar plot is constructed. If the fluorescence response to a repetitively intensity-modulated exciting light is defined over a definite period of repetition
is analyzed to extract the average fluorescence, phase delay, and amplitude of oscillation (modulation ratio); from these parameters, a polar plot is constructed. If the fluorescence response to a repetitively intensity-modulated exciting light is defined over a definite period of repetition 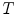 , a Fourier series analysis expands the measured repetitive fluorescent signal into a basis set of sine and cosine functions oscillating at a set of modulation frequencies
, a Fourier series analysis expands the measured repetitive fluorescent signal into a basis set of sine and cosine functions oscillating at a set of modulation frequencies 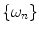 [9, 10],
[9, 10], 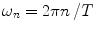 . The contribution of a specific repetitive frequency to the measured fluorescence (referred to as
. The contribution of a specific repetitive frequency to the measured fluorescence (referred to as 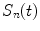 ) is defined by the coefficients
) is defined by the coefficients 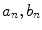 weighting the sine and cosine basis functions at each frequency
weighting the sine and cosine basis functions at each frequency 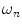 as shown in Eq. 2:
as shown in Eq. 2: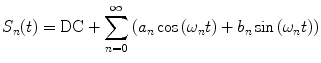
(2)
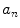 and
and 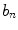 are defined in Eqs. 3 and 4.
are defined in Eqs. 3 and 4.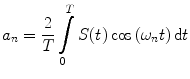
(3)
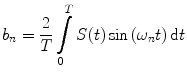
(4)
The nth component from the sum in Eq. 2 is an independent sinusoidal response representing the sample’s emitted fluorescence modulated at 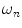 . This response is defined in terms of a modulation ratio
. This response is defined in terms of a modulation ratio 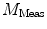 and phase delay
and phase delay 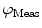 . For instance,
. For instance,
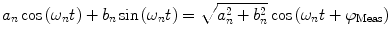
where
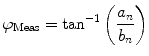
and 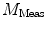 is defined as
is defined as
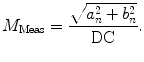
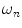 . This response is defined in terms of a modulation ratio
. This response is defined in terms of a modulation ratio 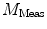 and phase delay
and phase delay 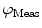 . For instance,
. For instance,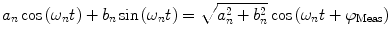
(5)
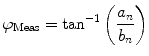
(6)
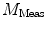 is defined as
is defined as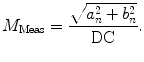
(7)
DC is the long time fluorescence intensity. The measured amplitude of oscillation (modulation ratio) 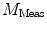 and phase delay
and phase delay 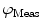 from a specific sample will depend on the instrument used for acquisition. The measurements taken on a given instrument depend on the excitation source, the sample holder (e.g., type/size of cuvette) and, in some cases, the gain of the detector. Therefore, the values for
from a specific sample will depend on the instrument used for acquisition. The measurements taken on a given instrument depend on the excitation source, the sample holder (e.g., type/size of cuvette) and, in some cases, the gain of the detector. Therefore, the values for 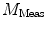 and
and 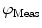 need to be corrected by analyzing the excitation light in order to relate them to the lifetime of the sample.
need to be corrected by analyzing the excitation light in order to relate them to the lifetime of the sample.
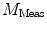 and phase delay
and phase delay 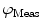 from a specific sample will depend on the instrument used for acquisition. The measurements taken on a given instrument depend on the excitation source, the sample holder (e.g., type/size of cuvette) and, in some cases, the gain of the detector. Therefore, the values for
from a specific sample will depend on the instrument used for acquisition. The measurements taken on a given instrument depend on the excitation source, the sample holder (e.g., type/size of cuvette) and, in some cases, the gain of the detector. Therefore, the values for 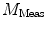 and
and 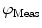 need to be corrected by analyzing the excitation light in order to relate them to the lifetime of the sample.
need to be corrected by analyzing the excitation light in order to relate them to the lifetime of the sample.The waveform of the excitation light is decomposed with a similar Fourier analysis, and analogous values for the modulation ratio 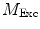 and phase delay
and phase delay 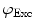 are defined. The variables
are defined. The variables 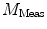 and
and 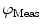 are then corrected in order to extract the modulation ratio
are then corrected in order to extract the modulation ratio 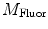 and phase delay
and phase delay 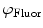 dependent on the lifetimes of the sample, Eqs. 8 and 9.
dependent on the lifetimes of the sample, Eqs. 8 and 9.
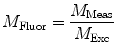
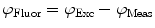
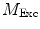 and phase delay
and phase delay 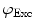 are defined. The variables
are defined. The variables 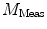 and
and 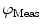 are then corrected in order to extract the modulation ratio
are then corrected in order to extract the modulation ratio 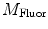 and phase delay
and phase delay 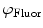 dependent on the lifetimes of the sample, Eqs. 8 and 9.
dependent on the lifetimes of the sample, Eqs. 8 and 9.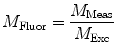
(8)
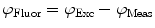
(9)
Values for 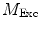 and
and 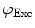 are commonly determined by measuring a sample with known modulation ratio and phase decay.
are commonly determined by measuring a sample with known modulation ratio and phase decay.
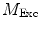 and
and 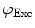 are commonly determined by measuring a sample with known modulation ratio and phase decay.
are commonly determined by measuring a sample with known modulation ratio and phase decay.If the sample is characterized by only a single exponential decay (lifetime), 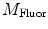 and
and 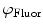 can be expressed as Eqs. 10 and 11,
can be expressed as Eqs. 10 and 11,
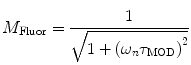
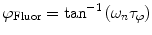
where  and
and 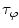 are both equal to the lifetime of the sample. If the sample is characterized by multiple exponential decays,
are both equal to the lifetime of the sample. If the sample is characterized by multiple exponential decays,  and
and 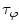 do not refer to any particular constituent decay.
do not refer to any particular constituent decay.
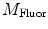 and
and 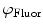 can be expressed as Eqs. 10 and 11,
can be expressed as Eqs. 10 and 11,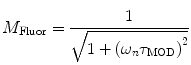
(10)
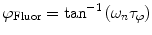
(11)
 and
and 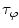 are both equal to the lifetime of the sample. If the sample is characterized by multiple exponential decays,
are both equal to the lifetime of the sample. If the sample is characterized by multiple exponential decays,  and
and 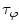 do not refer to any particular constituent decay.
do not refer to any particular constituent decay.Experimentally, instruments that measure lifetimes in the frequency domain directly output values for the oscillation (modulation) frequency 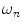 , the modulation ratio
, the modulation ratio 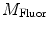 , and phase delay of the sample
, and phase delay of the sample 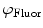 . Equivalently, Fourier analysis can be applied to the exponential decays produced by instruments operating in the time domain to find
. Equivalently, Fourier analysis can be applied to the exponential decays produced by instruments operating in the time domain to find 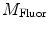 and
and 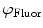 .
.
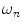 , the modulation ratio
, the modulation ratio 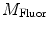 , and phase delay of the sample
, and phase delay of the sample 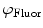 . Equivalently, Fourier analysis can be applied to the exponential decays produced by instruments operating in the time domain to find
. Equivalently, Fourier analysis can be applied to the exponential decays produced by instruments operating in the time domain to find 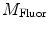 and
and 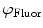 .
.2.3 Polar Plot
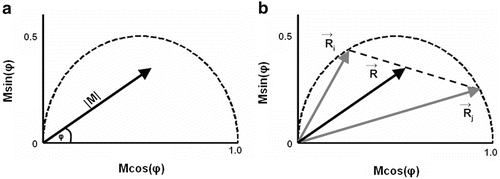
As demonstrated in Fig. 1a, the polar coordinates of any fluorescing species characterized by a single lifetime (single exponential decay) will reside on a semicircle with a radius of 0.5 centered at (0.5,0). If the sample contains multiple fluorescing species with different lifetimes, the 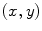 coordinates of the polar plot reflect the contributions of the constituent lifetimes,
coordinates of the polar plot reflect the contributions of the constituent lifetimes,
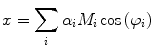
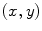 coordinates of the polar plot reflect the contributions of the constituent lifetimes,
coordinates of the polar plot reflect the contributions of the constituent lifetimes,
Fig. 1
Basics of the polar plot. (a) The polar coordinate of any fluorophore can be equivalently described as a vector with a length equal to the modulation ratio making an angle relative to the x-axis equal to the phase delay. (b) The polar coordinates of two different fluorophores defined by the vectors 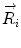 and
and 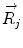 contribute intensity to the measured polar coordinate
contribute intensity to the measured polar coordinate 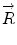 . All possible measured combinations of the two fluorophores
. All possible measured combinations of the two fluorophores 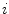 and
and 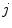 lie on the dashed line projected within the semicircle
lie on the dashed line projected within the semicircle
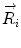 and
and 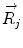 contribute intensity to the measured polar coordinate
contribute intensity to the measured polar coordinate 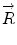 . All possible measured combinations of the two fluorophores
. All possible measured combinations of the two fluorophores 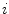 and
and 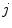 lie on the dashed line projected within the semicircle
lie on the dashed line projected within the semicircle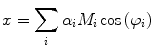
(14)