(1)
Faculty of Science, Department of Chemistry, Mahasarakham University, Mahasarakham, Thailand
(2)
Faculty of Science, Department of Chemistry, Chulalongkorn University, Bangkok, Thailand
(3)
Faculty of Science, Department of Chemistry, Center of Excellence for Petroleum, Petrochemicals, and Advanced Materials, Chulalongkorn University, Bangkok, Thailand
(4)
Division of Laser BioScience, Institute for Laser Technology, Osaka, Japan
Abstract
A method of analysis is described on the photoinduced electron transfer (PET) from aromatic amino acids as tryptophans (Trp) and tyrosines (Tyr) to the excited isoalloxazine (Iso*) in FMN-binding proteins (FBP) from Desulfovibrio vulgaris (strain, Miyazaki F). Time-dependent geometrical factors as the donor–acceptor distances are determined by means of a molecular dynamics simulation (MDS) of the proteins. Fluorescence decays of the single mutated isoforms of FBP are used as experimental data. The electrostatic (ES) energy between the photoproducts and ionic groups in the proteins is introduced into the Kakitani and Mataga (KM) model, which is modeled for an electron transfer process in solution. The PET parameters contained in the KM rate are determined by means of a nonlinear least square method, according to the Marquardt algorithm. The agreement between the observed and calculated decays is quite good, but not optimal. Characteristics on PET in flavoproteins, obtained by the present method, are described. Possible improvements of the method are discussed.
Key words
FlavinFlavoproteinPhotoinduced electron transferExcited isoalloxazine as acceptorTryptophan and tyrosine as donorMarcus–Hush theoryKakitani–Mataga theoryUltrafast fluorescence dynamicsMolecular dynamics simulationCalculated fluorescence decayElectrostatic energy between photoproducts and ionic groups inside protein1 Introduction
Flavoprotein was first discovered as a yellow pigment in cow milk in 1879 according to Massey [1]. By the early 1930s, this pigment had been recognized as a component of vitamin B2. The chemical structure of the pigment was identified, and it was named as riboflavin in 1934 [1] (see Fig. 1). The chromophore of flavins is the isoalloxazine ring (Iso). Theorell first isolated a yellow-colored yeast protein and found that the pigment is a cofactor of the protein [2]. Today, it is known that flavoproteins function as electron transport carrier, oxidase, oxygenase, dehydrogenase, etc. [3].
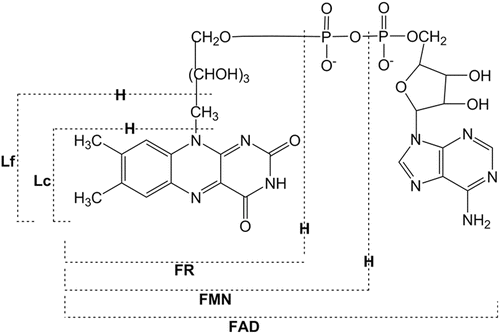

Fig. 1
Chemical structures of flavins. FR, riboflavin; FMN, flavin mononucleotide; FAD, flavin adenine dinucleotide; Lf, lumiflavin; Lc, lumichrome
Characterization of the photochemistry of flavins and flavoproteins had been pioneered by Weber, who first quantitatively studied the fluorescence of riboflavin for his Ph.D. work in 1947 [4]. Weber also studied the fluorescence quenching of flavins by various substances [5, 6]. The quenching mechanism of Iso fluorescence upon complex formation with adenine was first characterized by means of fluorescence lifetime measurements [7, 8]. McCormick studied the fluorescence quenching of Iso by indole with Iso-(CH2) n -indole diads [9]. Time-resolved fluorescence of flavins and flavoproteins has been reviewed by van den Berg and Visser [10].
In the last decade a number of new flavoproteins has been found, which function as photoreceptors [11]. Among six families of the photoreceptors, phototropins [12], cryptochromes [13], and BLUF (blue-light sensing using flavin) contain flavins as the reaction center [14]. Cryptochromes are blue-light receptors for development processes such as hypocotyl elongation in plants and circadian rhythm in plants and insects [13, 15]. The BLUF unit of AppA is involved in the repression of photosynthesis genes (PpsR) located at N-terminal region of the AppA protein from Rhodobacter sphaeroides [16]. The BLUF in TePixD from the thermophilic unicellular cyanobacterium Thermosynechococcus elongatus BP-1 regulates pili-dependent cell mobility [17]. In these BLUFs, the initial step of the photoreceptor functions is considered to be photoinduced electron transfer (PET) from the essential tyrosine (Tyr) to the excited isoalloxazine (Iso*) through hydrogen bonding (H bond) with glutamine (Gln). Thus, photochemistry and photophysics of flavins is becoming an important field of science [18].
The fluorescence quenching mechanism was first studied in systems of riboflavin tetrabutyrate with indole or N,N′-dimethylaniline in organic solvents [19] and in flavodoxin from Desulfovibrio vulgaris (strain, Miyazaki F) [20] by means of picosecond transient-absorption spectroscopy. It is concluded that the remarkable quenching of Iso fluorescence can be ascribed to photoinduced electron transfer (PET) from indole, N,N′-dimethylaniline, and Trp to the Iso*. The PET mechanism in riboflavin-binding protein from egg white was also reported in the femtosecond time domain by means of transient-absorption spectroscopy [21]. A number of flavoproteins display apparently no fluorescence. However, they exhibit fluorescence decays with ultrashort lifetimes upon excitation with a sub-picosecond pulse laser [22–29].
Since the seminal works on electron transfer theory by Marcus [30–32], several research workers further developed the theory [33–38]. These theories were modeled for electron transfer processes in solution. Hush introduced a donor–acceptor distance dependence into the electronic coupling term of the electron transfer rate [39]. The resulting equation is called Marcus–Hush theory [40]. The electron transfer theory in proteins has been worked out by Warshel et al. [41–43] and Beratan et al. [44]. Experimental studies on the electron transfer processes in proteins have been reviewed by Bendall [45] and by Gray and Winkler [46].
Transient fluorescence spectroscopy is a most useful experimental method to study the PET mechanism in flavoproteins. The ultrafast fluorescence of flavoproteins often decays with non-exponential functions. However, it has been difficult to obtain the PET rates from the fluorescence decay function, because any PET theory contains several unknown parameters, which cannot be determined by experiments. We have been developing a new method to evaluate the PET parameters contained in the analytical PET theories and, consequently, the PET rate [47–53]. In this method the Kakitani and Mataga (KM) model [36–38] was used, because it could satisfactorily reproduce the experimental fluorescence decays of flavoproteins.
In this chapter we describe a method to obtain the calculated fluorescence decays of FMN-binding proteins (FBP) from Desulfovibrio vulgaris (strain, Miyazaki F). FBP is a small flavoprotein, which contains FMN as cofactor and which is considered to play an important role in the electron transport process among bacterial proteins [54]. The three-dimensional structures of wild-type (WT) FBP were determined by NMR spectroscopy [55] and X-ray crystallography [56]. According to these structures, tryptophan 32 (Trp32) is closest to Iso and then tyrosine 35 (Tyr35) and Trp106 among the aromatic amino acids. Ultrafast fluorescence dynamics of WT FBP [27] and E13T (Glu13 was replaced by Thr), E13Q (Glu13 replaced by Gln), W32Y (Trp32 replaced by Tyr), and W32A (Trp32 replaced by Ala) FBP isoforms [28, 29] were measured by means of a fluorescence up-conversion method. These decays were simultaneously analyzed to obtain PET rate from individual donor and related physical quantities [49]. The limitations and possible improvements of the method are discussed in the Subheading 4.
2 Method of Analyses
2.1 Outline of the Method
The principle of the method to calculate the fluorescence decay, PET rate, and related physical quantities are illustrated in Fig. 2. More precise procedures are described below.
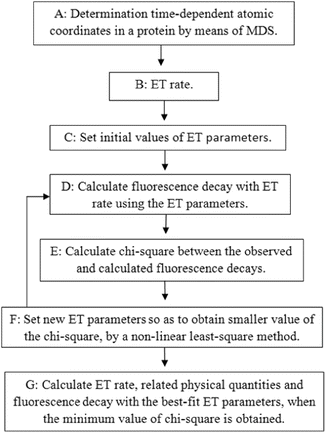

Fig. 2
Schematic diagram for the determination of PET rate and related physical quantities. Details of Procedures A–G are described in the text
Procedure A: The time-dependent atomic coordinates in the flavoproteins are determined by molecular dynamics simulation (MDS).
Procedure B: Any PET rates contain several unknown parameters (PET parameters). The PET rate by the KM model is given by Eq. 1.
Procedure C: Initial values of all PET parameters are set, which are dependent on the model used. Sometimes plausible values obtained by earlier works are chosen as the initial values.
Procedure D: The fluorescence decay is calculated with Eq. 7. In the primary process before taking the average with the MDS-snapshot ensemble, the probability of Iso* should decrease with a simple exponential function of the sum of the PET rates from potential PET donors. The PET rate itself is time independent. However, it becomes time dependent on the MDS time (t′), because the rate is dependent on the atomic coordinates, which vary with the MDS time. The calculated decay function is obtained by taking the average over the MDS time.
Procedure E: The chi-square is calculated between the calculated and experimental decay functions by Eq. 8.
Procedure F: A new set of PET parameters is obtained by a nonlinear least square method, which gives a lower value for the chi-square than the previous value. Procedures D to F are repeated until the minimum value of the chi-square is obtained.
Procedure G: The calculated decay, PET rates, and related physical quantities are obtained when the value of the chi-square becomes the minimum. These procedures are repeated with several models to obtain better fitting of the calculated decay with the observed decay.
All calculations of these procedures are performed with a personal computational program written with a BASIC compiler.
2.2 Determination of Atomic Coordinates in Five FBP Isoforms by Means of MDS
The starting structures of the WT and its mutated FBPs are obtained by using the X-ray structure of the D. vulgaris (strain Miyazaki F) WT FBP (PDB code 1FLM) [56]. In the E13T and E13Q single substitution isomers, the glutamate (E) at position 13 is replaced by threonine (T) and glutamine (Q), respectively, and the replacements of amino acids from the WT are conducted using the LEap module implemented in AMBER 8 [57]. All calculations are carried out using the AMBER 8 suite of programs. The parm99 force field [58] is used to describe the protein atoms, whereas force field parameters for Iso are obtained from the work by Schneider and Suhnel [59]. All missing hydrogen atoms of the protein are added using the LEap module of AMBER 8. The simulated systems are subsequently solvated with a cubic box of 6,336 TIP3P water molecules in WT, E13T, and E13Q, 6,345 in W32Y, and 6,347 in W32A. One chloride counterion is added to electronically neutralize the system. The total energy of the added water molecules is first minimized, while the protein and Iso coordinates are kept fixed. The entire system is then optimized using 2,000 steps of steepest descent and conjugated gradient minimizations. Afterwards, the whole system was heated from 10 K to 298 K over 50 ps and is further equilibrated under periodic boundary conditions at 298 K. The systems are set up under the isobaric–isothermal ensemble (NPT) with a constant pressure of 1 atm and constant temperature of 298 K. The electrostatic interaction is corrected by the Particle Mesh Ewald method [60]. The SHAKE algorithm [61] is employed to constrain all bonds involving hydrogen atoms. A cutoff distance of 1 nm is employed for nonbonded pair interactions. MDS based calculations are performed with time steps of 2 fs and the coordinates of the MDS snapshots are collected every 0.01 ps. The simulations are performed over 5 ns. Data collected during the last 2–3 ns are used for the analysis.
2.3 PET Rate
Here 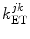 is the PET rate constant of donor k in jth FBP isoform. k = 1 for Trp32 (Tyr32 in W32Y), k = 2 for Tyr35, and k = 3 for Trp106. j = 1 for WT, j = 2 for E13T, j = 3 for E13Q, j = 4 for W32Y, and j = 5 for W32A FBP.
is the PET rate constant of donor k in jth FBP isoform. k = 1 for Trp32 (Tyr32 in W32Y), k = 2 for Tyr35, and k = 3 for Trp106. j = 1 for WT, j = 2 for E13T, j = 3 for E13Q, j = 4 for W32Y, and j = 5 for W32A FBP. 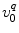 is an adiabatic frequency,
is an adiabatic frequency, 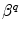 is the PET process coefficient, and
is the PET process coefficient, and 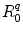 is a critical distance between the adiabatic and nonadiabatic PET processes. It was assumed that these quantities depend only on q (Trp or Tyr), not on j and k. When
is a critical distance between the adiabatic and nonadiabatic PET processes. It was assumed that these quantities depend only on q (Trp or Tyr), not on j and k. When 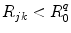 , the PET process is adiabatic, whereas when
, the PET process is adiabatic, whereas when 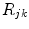 is the center-to-center distance (often Rc is used for it) between Iso and the PET donor k in the jth FBP system. The physical constants k B , T, and e are Boltzmann constant, temperature (298 K), and electron charge, respectively.
is the center-to-center distance (often Rc is used for it) between Iso and the PET donor k in the jth FBP system. The physical constants k B , T, and e are Boltzmann constant, temperature (298 K), and electron charge, respectively. 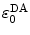 is a static dielectric constant of medium between PET donors and acceptor.
is a static dielectric constant of medium between PET donors and acceptor. 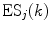 is a net electrostatic (ES) energy between the kth aromatic ionic species and all other ionic groups in the jth FBP isoform, as described below.
is a net electrostatic (ES) energy between the kth aromatic ionic species and all other ionic groups in the jth FBP isoform, as described below. 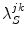 is the solvent reorganization energy [30, 31] of the Iso* and the kth donor in the jth FBP isoform, as shown by Eq. 2:
is the solvent reorganization energy [30, 31] of the Iso* and the kth donor in the jth FBP isoform, as shown by Eq. 2:
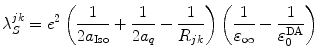
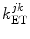 is the PET rate constant of donor k in jth FBP isoform. k = 1 for Trp32 (Tyr32 in W32Y), k = 2 for Tyr35, and k = 3 for Trp106. j = 1 for WT, j = 2 for E13T, j = 3 for E13Q, j = 4 for W32Y, and j = 5 for W32A FBP.
is the PET rate constant of donor k in jth FBP isoform. k = 1 for Trp32 (Tyr32 in W32Y), k = 2 for Tyr35, and k = 3 for Trp106. j = 1 for WT, j = 2 for E13T, j = 3 for E13Q, j = 4 for W32Y, and j = 5 for W32A FBP. 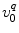 is an adiabatic frequency,
is an adiabatic frequency, 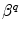 is the PET process coefficient, and
is the PET process coefficient, and 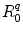 is a critical distance between the adiabatic and nonadiabatic PET processes. It was assumed that these quantities depend only on q (Trp or Tyr), not on j and k. When
is a critical distance between the adiabatic and nonadiabatic PET processes. It was assumed that these quantities depend only on q (Trp or Tyr), not on j and k. When 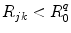 , the PET process is adiabatic, whereas when
, the PET process is adiabatic, whereas when 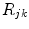 is the center-to-center distance (often Rc is used for it) between Iso and the PET donor k in the jth FBP system. The physical constants k B , T, and e are Boltzmann constant, temperature (298 K), and electron charge, respectively.
is the center-to-center distance (often Rc is used for it) between Iso and the PET donor k in the jth FBP system. The physical constants k B , T, and e are Boltzmann constant, temperature (298 K), and electron charge, respectively. 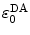 is a static dielectric constant of medium between PET donors and acceptor.
is a static dielectric constant of medium between PET donors and acceptor. 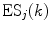 is a net electrostatic (ES) energy between the kth aromatic ionic species and all other ionic groups in the jth FBP isoform, as described below.
is a net electrostatic (ES) energy between the kth aromatic ionic species and all other ionic groups in the jth FBP isoform, as described below. 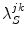 is the solvent reorganization energy [30, 31] of the Iso* and the kth donor in the jth FBP isoform, as shown by Eq. 2:
is the solvent reorganization energy [30, 31] of the Iso* and the kth donor in the jth FBP isoform, as shown by Eq. 2: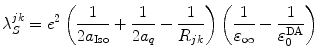
(2)
Here, 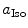 and
and 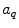 are the radii of Iso and the donor q (Trp or Tyr), assuming these reactants are spherical, and
are the radii of Iso and the donor q (Trp or Tyr), assuming these reactants are spherical, and 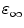 is the optical dielectric constant (a value of 2 being used). The radii of Iso, Trp, and Tyr were determined in the following way: (1) Three-dimensional sizes of lumiflavin for Iso, 3-methylindole for Trp, and p-methylphenol for Tyr were obtained by a semiempirical molecular orbital method (PM3). (2) The volumes of these molecules were determined as asymmetric rotors. (3) Radii of the spheres having the same volumes as the asymmetric rotors were obtained.
is the optical dielectric constant (a value of 2 being used). The radii of Iso, Trp, and Tyr were determined in the following way: (1) Three-dimensional sizes of lumiflavin for Iso, 3-methylindole for Trp, and p-methylphenol for Tyr were obtained by a semiempirical molecular orbital method (PM3). (2) The volumes of these molecules were determined as asymmetric rotors. (3) Radii of the spheres having the same volumes as the asymmetric rotors were obtained. 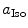 is 0.224 nm,
is 0.224 nm, 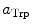 0.196 nm, and
0.196 nm, and 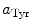 0.173 nm.
0.173 nm.
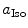 and
and 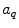 are the radii of Iso and the donor q (Trp or Tyr), assuming these reactants are spherical, and
are the radii of Iso and the donor q (Trp or Tyr), assuming these reactants are spherical, and 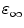 is the optical dielectric constant (a value of 2 being used). The radii of Iso, Trp, and Tyr were determined in the following way: (1) Three-dimensional sizes of lumiflavin for Iso, 3-methylindole for Trp, and p-methylphenol for Tyr were obtained by a semiempirical molecular orbital method (PM3). (2) The volumes of these molecules were determined as asymmetric rotors. (3) Radii of the spheres having the same volumes as the asymmetric rotors were obtained.
is the optical dielectric constant (a value of 2 being used). The radii of Iso, Trp, and Tyr were determined in the following way: (1) Three-dimensional sizes of lumiflavin for Iso, 3-methylindole for Trp, and p-methylphenol for Tyr were obtained by a semiempirical molecular orbital method (PM3). (2) The volumes of these molecules were determined as asymmetric rotors. (3) Radii of the spheres having the same volumes as the asymmetric rotors were obtained. 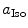 is 0.224 nm,
is 0.224 nm, 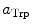 0.196 nm, and
0.196 nm, and 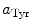 0.173 nm.
0.173 nm.2.4 Electrostatic Energy in the Proteins
Proteins, including FBPs, contain many ionic groups, which may influence the PET rate. The cofactor in all these FBP systems is FMN, which has two negative charges at the phosphate group. The WT, W32Y, and W32A contain eight Glu, five Asp, four Lys, and nine Arg residues, whereas E13T and E13Q contain seven Glu, five Asp, four Lys, and nine Arg residues, since the Glu13 is replaced by the neutral Thr13 and Gln13, respectively. The ES energy between the Iso anion or kth donor cation and all other ionic groups in jth isoform is expressed by Eq. 4:
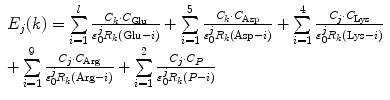
where n = 8 for the WT, W32Y, and W32A, while l = 7 for E13T and E13Q. Here, k = 0 for the Iso−, k = 1 for Trp32+, k = 2 for Tyr35+, and k = 3 for Trp106+. 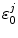 is the static dielectric constant inside the jth isoform.
is the static dielectric constant inside the jth isoform. 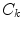 is the charge of the aromatic ionic species k and is −e for k = 0 (Iso anion) and +e for k = 1–3.
is the charge of the aromatic ionic species k and is −e for k = 0 (Iso anion) and +e for k = 1–3. 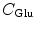 (= −e),
(= −e), 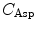 (= −e),
(= −e), 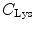 (= +e),
(= +e), 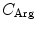 (= +e), and
(= +e), and 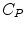 (= −e) are the charges of Glu, Asp, Lys, Arg, and phosphate anions, respectively. We assume that these groups are all in an ionic state in solution. The values of pK a of ionic amino acids in water are 4.3 in Glu, 3.9 in Asp, 10.5 in Lys, and 12.5 in Arg. In the proteins these values of pK a may be modified in the range of ±0.3. Histidine (His) displays a pK a of 6.0 in water. All measurements were performed in a 10 mM Tris–HCl buffer (pH 8.0) containing 200 mM NaCl, in which His should be neutral. Distances between the aromatic ionic species k and the ith Glu (i = 1–8 or 7) are denoted as
(= −e) are the charges of Glu, Asp, Lys, Arg, and phosphate anions, respectively. We assume that these groups are all in an ionic state in solution. The values of pK a of ionic amino acids in water are 4.3 in Glu, 3.9 in Asp, 10.5 in Lys, and 12.5 in Arg. In the proteins these values of pK a may be modified in the range of ±0.3. Histidine (His) displays a pK a of 6.0 in water. All measurements were performed in a 10 mM Tris–HCl buffer (pH 8.0) containing 200 mM NaCl, in which His should be neutral. Distances between the aromatic ionic species k and the ith Glu (i = 1–8 or 7) are denoted as 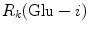 , those between kth ion and the ith Asp (i = 1–5) are denoted as
, those between kth ion and the ith Asp (i = 1–5) are denoted as 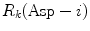 , and so on.
, and so on.
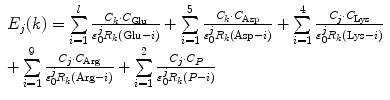
(4)
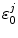 is the static dielectric constant inside the jth isoform.
is the static dielectric constant inside the jth isoform. 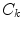 is the charge of the aromatic ionic species k and is −e for k = 0 (Iso anion) and +e for k = 1–3.
is the charge of the aromatic ionic species k and is −e for k = 0 (Iso anion) and +e for k = 1–3. 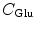 (= −e),
(= −e), 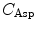 (= −e),
(= −e), 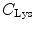 (= +e),
(= +e), 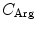 (= +e), and
(= +e), and 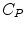 (= −e) are the charges of Glu, Asp, Lys, Arg, and phosphate anions, respectively. We assume that these groups are all in an ionic state in solution. The values of pK a of ionic amino acids in water are 4.3 in Glu, 3.9 in Asp, 10.5 in Lys, and 12.5 in Arg. In the proteins these values of pK a may be modified in the range of ±0.3. Histidine (His) displays a pK a of 6.0 in water. All measurements were performed in a 10 mM Tris–HCl buffer (pH 8.0) containing 200 mM NaCl, in which His should be neutral. Distances between the aromatic ionic species k and the ith Glu (i = 1–8 or 7) are denoted as
(= −e) are the charges of Glu, Asp, Lys, Arg, and phosphate anions, respectively. We assume that these groups are all in an ionic state in solution. The values of pK a of ionic amino acids in water are 4.3 in Glu, 3.9 in Asp, 10.5 in Lys, and 12.5 in Arg. In the proteins these values of pK a may be modified in the range of ±0.3. Histidine (His) displays a pK a of 6.0 in water. All measurements were performed in a 10 mM Tris–HCl buffer (pH 8.0) containing 200 mM NaCl, in which His should be neutral. Distances between the aromatic ionic species k and the ith Glu (i = 1–8 or 7) are denoted as 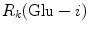 , those between kth ion and the ith Asp (i = 1–5) are denoted as
, those between kth ion and the ith Asp (i = 1–5) are denoted as 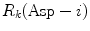 , and so on.
, and so on.Here, j varies from 1 to 5.
2.5 Fluorescence Decays
The ultrafast fluorescence dynamics of the WT FBP [27], W32Y and W32A [28], and E13T and E13Q FBP isoforms [29] were obtained by Chosrowjan and coworkers by means of the fluorescence up-conversion method. The fluorescence decay functions of these flavoproteins are expressed by multiple-exponential function as Eq. 6. The pre-exponential factor (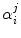 ) of the ith lifetime component (
) of the ith lifetime component (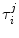 ) in the jth isoform is given in Table 1. The lifetimes are expressed in units of picoseconds:
) in the jth isoform is given in Table 1. The lifetimes are expressed in units of picoseconds:
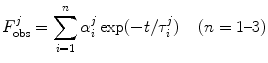
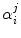 ) of the ith lifetime component (
) of the ith lifetime component (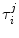 ) in the jth isoform is given in Table 1. The lifetimes are expressed in units of picoseconds:
) in the jth isoform is given in Table 1. The lifetimes are expressed in units of picoseconds:Table 1
Experimental decay parameters in five FBP isoforms
FBP | 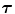 1 1 (ps) | ( 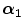 ) ) | 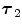 (ps) | ( 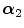 ) ) | 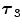 (ps) | ( 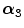 ) ) | 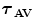 a a (ps) |
|---|---|---|---|---|---|---|---|
WTb | 0.167 | (0.96) | 1.5 | (0.04) | – | – | 0.220 |
E13Tc | 0.107 | (0.86) | 1.5 | (0.12) | 30 | (0.02) | 0.872 |
E13Qc | 0.134 | (0.85) | 0.746 | (0.12) | 30 | (0.03) | 1.10 |
W32Yd | 3.4 | (0.23) | 18.2 | (0.74) | 96 | (0.03) | 17.1 |
W32Ad | 30.1 | (1.00) | – | – | – | – | 30.1 |
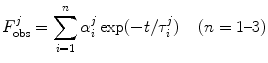
(6)
The fluorescence decays of FBP isoforms are calculated up to 3 ps with 0.003 ps time intervals. The fluorescence decays of the WT, E13T, and E13Q FBP isoforms are calculated up to 3 ps with 0.003 ps time intervals, while that for the W32Y and W32A isoforms are calculated up to 20 ps with 0.02 ps intervals. Note that 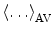 denotes the averaging procedure of the exponential function in Eq. 7, which is performed over
denotes the averaging procedure of the exponential function in Eq. 7, which is performed over 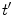 up to 2 ns with 0.1 ps time intervals for the WT, W32Y, and W32A isoforms and up to 3 ns with 0.1 ps intervals for the E13T and E13Q isoforms. In Eq. 7 we assume that the decay functions at every instant of time (t′) during the MDS time range can always be expressed by an exponential function. The present method is equivalent to the reported one [63] when the time range (t′ = 2–3 ns) of MDS data is much longer than that for the fluorescence data (t is at most 20 ps) [48].
up to 2 ns with 0.1 ps time intervals for the WT, W32Y, and W32A isoforms and up to 3 ns with 0.1 ps intervals for the E13T and E13Q isoforms. In Eq. 7 we assume that the decay functions at every instant of time (t′) during the MDS time range can always be expressed by an exponential function. The present method is equivalent to the reported one [63] when the time range (t′ = 2–3 ns) of MDS data is much longer than that for the fluorescence data (t is at most 20 ps) [48].
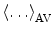 denotes the averaging procedure of the exponential function in Eq. 7, which is performed over
denotes the averaging procedure of the exponential function in Eq. 7, which is performed over 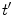 up to 2 ns with 0.1 ps time intervals for the WT, W32Y, and W32A isoforms and up to 3 ns with 0.1 ps intervals for the E13T and E13Q isoforms. In Eq. 7 we assume that the decay functions at every instant of time (t′) during the MDS time range can always be expressed by an exponential function. The present method is equivalent to the reported one [63] when the time range (t′ = 2–3 ns) of MDS data is much longer than that for the fluorescence data (t is at most 20 ps) [48].
up to 2 ns with 0.1 ps time intervals for the WT, W32Y, and W32A isoforms and up to 3 ns with 0.1 ps intervals for the E13T and E13Q isoforms. In Eq. 7 we assume that the decay functions at every instant of time (t′) during the MDS time range can always be expressed by an exponential function. The present method is equivalent to the reported one [63] when the time range (t′ = 2–3 ns) of MDS data is much longer than that for the fluorescence data (t is at most 20 ps) [48].Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


![$$ \begin{array}{ll}k_{\mathrm{ ET}}^{jk }=\frac{{v_0^q}}{{1+\exp \left\{ {{\beta^q}({R_{jk }}-R_0^q)} \right\}}}\sqrt{{\frac{{{k_B}T}}{{4\pi \lambda_S^{jk }}}}}\\ \times\exp \left[ {-\frac{{{{{\left\{ {\varDelta G_q^0-{e^2}/\varepsilon_0^{\mathrm{ DA}}{R_{jk }}+\lambda_S^{jk }+\mathrm{ E}{{\mathrm{ S}}_j}(k)} \right\}}}^2}}}{{4\lambda_S^{jk }{k_B}T}}} \right]\end{array} $$](/wp-content/uploads/2017/03/A299540_1_En_14_Chapter_Equ00141.gif)
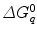
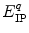
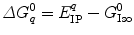
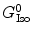
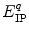
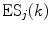
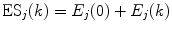
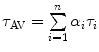
![$$ F_{\mathrm{ calc}}^j(t)={{\left\langle {\exp \left[ {-\left\{ {\sum\limits_{k=1}^3 {k_{\mathrm{ ET}}^k({t}^{\prime})} } \right\}t} \right]} \right\rangle}_{\mathrm{ AV}}} $$](/wp-content/uploads/2017/03/A299540_1_En_14_Chapter_Equ00147.gif)
