Table 2-1. Metric System Prefixes
Prefix | Meaning |
mega- | one million times the base unit (106) |
kilo- | one thousand times the base unit (103) |
deci- | one-tenth the base unit (10−1) |
centi- | one-hundredth the base unit (10−2) |
milli- | one-thousandth the base unit (10−3) |
micro- | one-millionth the base unit (10−6) |
nano- | one-billionth the base unit (10−9) |
pico- | one-trillionth the base unit (10−12) |
Table 2-2. Apothecaries’ System of Measure

Household Measures
A tablespoon is equivalent to 15 mL, and a teaspoon is equivalent to 5 mL.
Conversion Factors
A short list of convenient conversion factors follows:
1 inch = 2.54 cm
1 fl oz = 29.57 mL
1 g = 15.4 grains
1 kg = 2.20 lb (avoirdupois)
1 lb (avoirdupois) = 454 g
1 gal (U.S.) = 3,785 mL
2-4. Significant Figures
All measured quantities are approximations. The accuracy of a given measurement is conveyed by the number of figures that are recorded. The number of significant figures in a measurement includes the first approximate figure. The last recorded digit to the right of a measured quantity is taken to be an approximation. For example, the weight 13.24 g has four significant figures, and the final digit, 4, is approximate. Calculations should be conducted to carry the correct numbers of significant figures.
Frequently, the different quantities in a given calculation have different numbers of significant figures. When that occurs, the following rules apply.
Addition and Subtraction
When adding or subtracting decimal numbers, round all measurements so that they have the same number of decimal places as the least in the set. For example, 13.78 mL and 53.5 mL would be added as 13.8 mL + 53.5 mL = 67.3 mL, using and retaining only one decimal place.
Multiplication and Division
When multiplying or dividing decimal numbers, round the measurements to include the number of significant figures contained in the least accurate number. For example, 25.678 mL × 1.24 g/mL would be multiplied as 25.7 mL × 1.24 g/mL = 31.9 g, using and retaining three significant figures in each number.
Handling Zero
The digit zero may or may not be counted as a significant figure, depending on where it appears in the measured number. If zero occurs at an interior position in the number (e.g., 3,052 or 2.031), it is significant. If zero occurs as the last digit to the right of the decimal (e.g., 44.50), it is significant. If zero occurs as the first digit to the right of the decimal in a number that is less than 1, it is not significant. For example, in 0.078 there are only two significant figures. If zero occurs as the last digit, or digits, in a whole number (i.e., no decimal is expressed), its significance is unknown without further information. For example, 3,500 might have two, three, or four significant figures.
From a medication safety perspective, never use trailing zeros for drug doses expressed as a whole number (1.0 mg can be mistaken as 10 mg: use 1 mg). Always use a zero before the decimal point when the drug dose is less than 1 (.1 mg may be mistaken as 1 mg: use 0.1 mg).
2-5. Ratios and Proportions
Most dosage calculations in pharmacy use ratios and proportions. A ratio is used to convey the relationship between two quantities, and a proportion involves a relationship among four quantities. You can always solve for one of those quantities when the other three are known. If the ratio x/y is equal to the ratio a/b, then the proportion x/y = a/b exists, and x can be obtained by algebraic manipulation (x = ay/b). Such problems are frequently encountered when calculating doses.
One common source of error in proportion problems involves writing one of the ratios upside down (e.g., writing x/y = b/a, when it should be written x/y = a/b). A disciplined approach to setting up such problems can help. For example, you might establish a rule in which you express each ratio as the quotient of like quantities. If the numerator of one ratio is smaller (or larger) than its denominator, the same should be true of the other ratio.
Another source of error involves using mixed units (e.g., using one number expressed in grams and the other in milligrams). To guard against that kind of error, always write the units into the equation along with the numbers. All unit expressions should cancel except those required for the quantity being solved for (dimensional analysis).
Example: If 300 mL of a preparation contains 250 mg of drug, what weight of drug (x) is contained in 1,800 mL of the preparation?
Equate the ratios x: 250 mg and 1,800 mL: 300 mL to solve for x:
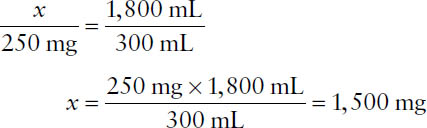
Note that because the new volume is six times greater, the new weight should be six times greater as well.
2-6. Specific Gravity and Density
At times, you will be required to convert a volume measure to a weight measure, or vice versa. This process is used by parenteral nutrition–compounding devices that prepare multicomponent intravenous solutions. To convert a measure, you will need to use either the specific gravity or the density of the material. The specific gravity (SpGr) is a ratio of the weight of the material to the weight of the same volume of a standard material. For liquids, the standard material is water, which has a density of 1 g/mL. Specific gravity is unitless. Density is the quotient of any measure of the weight of a sample of the material divided by any measure of the volume of the sample. The units must be explicitly expressed (e.g., g/mL, lb/gal, etc.). When density is expressed in grams per milliliter, it is numerically equal to specific gravity. Algebraically, density (weight/volume) is easier to work with than the corresponding expression for specific gravity.
Example: What are the volume and weight of 70% dextrose (D70) (SpGr = 1.24) that are required to prepare a parenteral nutrition solution that contains 210 g of dextrose?
Volume D70 = 210 g ÷ 0.7 g/mL = 300 mL
Weight D70 = 300 mL × 1.24 = 372 g
Thus, the parenteral nutrition compounder would weigh 372 g D70 to add 300 mL of D70 to provide 210 g of dextrose.
2-7. Percentage Error
Because all measurements are approximations, one must characterize the extent of error involved, or percentage of error, which is defined as
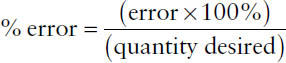
The term error in the numerator indicates the maximum potential error in the measurement (error = larger quantity – smaller quantity), while the term quantity desired in the denominator represents the total amount measured. Percentage of error may be calculated for either a weight or a volume measurement.
Example: A quantity of material weighs 5.81 g on a prescription balance. Using a much more accurate analytical balance, the quantity weighs 5.893 g. What is the percentage of error for the original weighing?
error = 5.893 g – 5.810 g = 0.083 g
The quantity desired is 5.81 g. Thus,
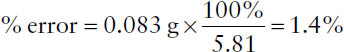
Example: Suppose you wish to weigh out 75 mg of an ingredient but mistakenly weigh 65 mg instead. Based on the quantity desired, what is the percentage of error?
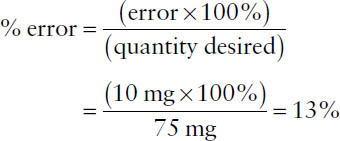
2-8. Minimum Measurable
By United States Pharmacopeia (USP) standards, weighing by a pharmacist cannot exceed a percentage of error greater than 5%, which requires that the sensitivity of the balance be known and limits the smallest quantity that can be weighed. Balance sensitivity is defined in terms of the sensitivity requirement (SR), which is the weight of material that will move the indicator one marked unit on the index plate of the balance. For a class A prescription balance, SR = 6 mg. The minimum weighable quantity for a given balance can be calculated using the percentage of error formula: replace the “error” term with the SR (e.g., 6 mg), replace the percentage of error term with 5%, and replace the “quantity desired” term with “minimum weighable quantity” as follows:
Example: For a balance that has an SR of 4 mg, what is the minimum weighable quantity to ensure a percentage of error no greater than 2%?

Example: What is the SR for a balance with a percentage of error of 5% when weighing 120 mg?
2-9. Patient-Specific Dosage Calculations
Drugs with a narrow therapeutic range often are dosed on the basis of patient weight or body surface area. For patients with renal impairment, some drugs are dosed on the basis of creatinine clearance.
Dosing Based on Body Weight
Weight-based dosing might involve using the patient’s actual body weight (ABW), ideal body weight (IBW), or perhaps an adjusted ideal body weight that is a function of IBW and ABW. Those weights are invariably expressed in kilograms.
Example: A patient weighing 180 lb is to receive 0.25 mg/kg per day amphotericin B (reconstituted and diluted to 0.1 mg/mL) by intravenous (IV) infusion. What volume of solution is required to deliver the daily dose?

A commonly used equation for calculating IBW is
IBW (kg) = (sex factor) + (2.3 × height in inches over 5 feet),
where the sex factor for males is 50 and the sex factor for females is 45.5.
Example: The recommended adult daily dosage for patients with normal renal function for tobramycin is 3 mg/kg IBW given in three evenly divided doses. What would the dose of each injection be for a male patient who weighs 185 lb and is 5 feet 9 inches tall?
In the absence of other information, the usual drug doses are considered generally suitable for 70-kg individuals. Thus, in the absence of more specific information, an adjusted dosage for a notably larger or smaller individual may be obtained by multiplying the usual dose by the ratio of patient weight to 70 kg (Clark’s rule).
Example: If the adult dose of a drug is 100 mg and no child-specific dosing information is available, what would the weight-adjusted dose be for a child who weighs 40 kg?
Dosing Based on Body Surface Area
Dosing based on body surface area requires an estimation of the patient’s body surface area (BSA) expressed in square meters (m2). That parameter might be estimated from a nomogram using height and weight or, for adults, by using one of several equations such as the Mosteller equation:
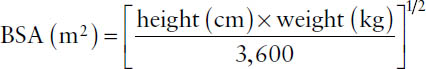
Example: What is the computed BSA for an adult who weighs 194 lb and is 5 feet 10 inches tall?
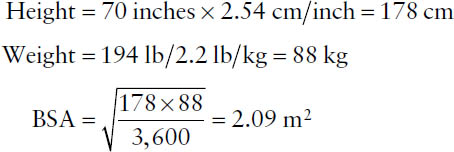
The average adult BSA is taken to be 1.73 m2. That value can be used to obtain an approximate child’s dose, given the usual dose for an adult and the child’s estimated BSA.
Example: If the adult dose of a drug is 50 mg, what would the BSA-adjusted dose be for a child having an estimated BSA of 0.55 m2?
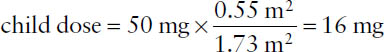
Dosing Based on Creatinine Clearance
For many drugs, the rate of elimination depends on kidney function. With a decline in kidney function, there is a decrease in drug clearance. Creatinine clearance (CrCl) estimates kidney function as a measure of the volume of blood plasma that is cleared of creatinine by kidney filtration per minute, and it is expressed in milliliters per minute. CrCl can be calculated as a function of patient sex, age, body weight, and serum creatinine using the Cockcroft–Gault equation for adults and the Schwartz equation for children.
The Cockcroft–Gault equation for males:
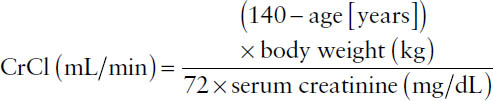
For females:
CrCl = 0.85 × CrCl for males
Example: Using the Cockcroft–Gault equation, calculate the creatinine clearance rate for a 76-year-old female weighing 65 kg and having a serum creatinine of 0.52 mg/dL.
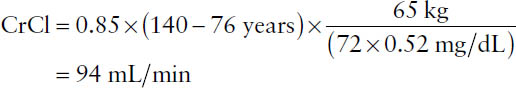
The Schwartz equation:
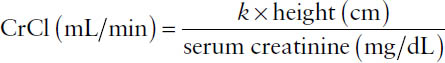
Age | k |
Premature infant < 1 year | 0.33 |
Term infant < 1 year | 0.45 |
Child or adolescent girl | 0.55 |
Adolescent boy | 0.7 |
The maintenance dose for some drugs is based on IBW and CrCl. See Chapter 7 for more detailed information.
2-10. Use of Batch Preparation Formulas
The relative amounts of ingredients in a pharmaceutical product are specified in a formula. A pharmacist may be required to reduce or enlarge the formula to prepare a lesser or greater amount of product. A given formula might specify either the actual amount (weight or volume) of each ingredient for a specified total amount of product or just the relative amount (part) of each ingredient. In the latter case, the ingredients must all be of the same measure (e.g., weight in grams).
Example: From the following lotion formula, calculate the quantity of triethanolamine required to make 200 mL of lotion.
Triethanolamine | 10 mL |
Oleic acid | 25 mL |
Benzyl benzoate | 250 mL |
Water ad | 1,000 mL |
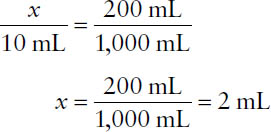
Example: From the following formula, calculate the quantity of chlorpheniramine maleate required to make 500 g of product.
Chlorpheniramine maleate | 6 parts |
Phenindamine | 20 parts |
Phenylpropanolamine HCl | 55 parts |
Note that the formula will give a total of 81 parts, which will correspond to the desired quantity of 500 g. Then,
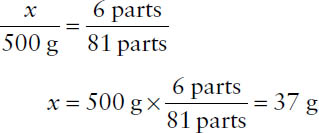
2-11. Conventions in Expression of Concentration
Drug concentrations can be expressed in a variety of units. One must be prepared to calculate drug concentration units directly from their definitions and to interconvert among them.
Percentage Strength
Percentage, strictly speaking, specifies the number of parts per 100 parts. In pharmacy, percentage comes in three varieties:
■ Percent weight-in-weight = % (w/w) = grams of ingredient in 100 grams of product (assumed for mixtures of solids and semisolids, e.g., ointment base)
■ Percent volume-in-volume = % (v/v) = milliliters of ingredient in 100 milliliters of product (assumed for solutions or mixtures of liquids)
■ Percent weight-in-volume = % (w/v) = grams of ingredient in 100 milliliters of product (assumed for solutions of solids in liquids)
Example: What is the concentration in % (w/v) for a preparation containing 250 mg of drug in 50 mL of solution? Note that % (w/v) is defined as g/100 mL. Thus,
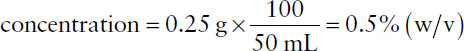
Parts (Ratio Strength)
Concentrations may be expressed in “parts” or ratio strength when the active ingredient is highly diluted. Assumptions concerning (w/w), (v/v), and (w/v) ratios are identical to those for percentages.
Example: What is the concentration in % (v/v) of a solution that has a ratio strength of 1:2,500 (v/v)?
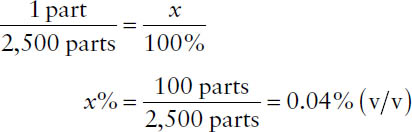
Millimoles
By definition, a 1 molar solution contains the molecular weight (MW) of the substance in grams per liter of solution. The molarity expresses the number of moles per liter. The millimolarity (millimoles/liter) is 1,000 times the molarity of a solution.
Example: What is the millimolar concentration of a solution consisting of 0.9 g of sodium chloride (MW = 58.5) in 100 mL of water? The quantity of 0.9 g in 100 mL corresponds to 9 g in 1,000 mL.
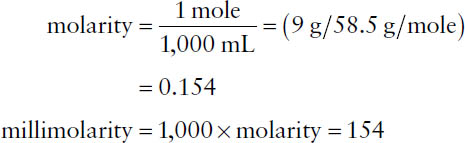
Milliequivalents
A milliequivalent is a measure of the total number of ionic charges in a solution. The equivalent weight of an ion is the molecular weight of the ion divided by the valence. Thus, the equivalent weight of sodium ion, Na+ (MW = 23, valence = 1), is 23 and for ferric ion, Fe3+ (MW = 55.9, valence = 3), 18.6. A milliequivalent is 1,000th of an equivalent weight (i.e., 1,000 milliequivalent weights equal 1 equivalent weight). For a molecule, the equivalent weight is obtained by dividing the molecular weight by the total valence of the positive or negative ion. For example, the equivalent weight of MgCl2 (MW Mg++ = 24.3, valence = 2; MW Cl− = 35.5, valence = 1) is (24.3 + 2 × 35.5)/2 = 47.7 g. Its milliequivalent weight is 0.0477 g, or 47.7 mg.
Example: What is the concentration, in milliequivalents per liter, of a solution containing 14.9 g of KCl (MW = 74.5 g) in 1 liter? Note that the valence of potassium is 1, so the equivalent weight equals the molecular weight. Accordingly,
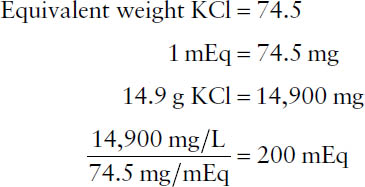
Example: What weight of MgSO4 (MW = 120) is required to prepare 1 liter of a solution that is 25 mEq/L? The valence of Mg is 2+; therefore, the equivalent weight of MgSO4 is 120/2 = 60 g. Accordingly, 60 mg corresponds to 1 mEq of MgSO4. Then,
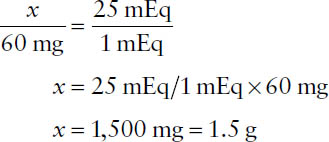
Example: How many milliequivalents of CaCl2 are contained in 100 mL of a solution that is 5.0% (w/v) (MW = 111, atomic weight of Ca2+ = 40, atomic weight of Cl− = 35.5)? Note that the valence of calcium is 2+; therefore, the milliequivalent weight of CaCl2 is 55.5 mg. The solution contains 5 g CaCl2 per 100 mL, which corresponds to 5,000 mg/100 mL and 5,000 mg/55.5 mg/mEq = 90 mEq. Thus, 100 mL of the 5% CaCl2 solution contains 90 mEq of Ca2+.
Milliosmoles
Osmotic concentration is a measure of the total number of particles in solution and is expressed in milliosmoles (mOsm). The number of milliosmoles is based on the total number of cations and the total number of anions. The milliosmolarity of a solution is the number of milliosmoles per liter of solution (mOsm/L), where
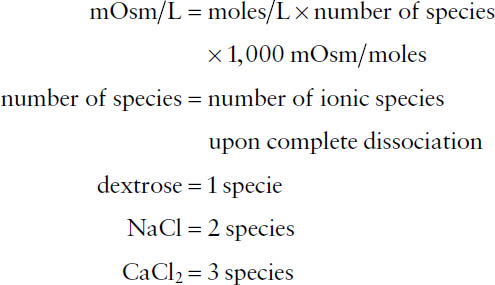
The total osmolarity of a solution is the sum of the osmolarities of the solute components of the solution. When calculating osmolarities, in the absence of other information, assume that salts (e.g., NaCl, etc.) dissociate completely (referred to as the ideal osmolarity). You should be aware of the distinction between the terms milliosmolarity (milliosmoles per liter of solution) and milliosmolality (milliosmoles per kilogram of solution).
Example: What is the concentration, in milliosmoles per liter, of a solution that contains 224 mg of KCl (MW = 74.6 g) and 234 mg of NaCl (MW = 58.5) in 500 mL? What is the number of milliosmoles per liter of K+ alone?

Milligrams per 100 Milliliters and Milligrams per Deciliter
Certain laboratory test values are reported as the number of milligrams per deciliter (mg/dL) or milligrams percent (mg%), which is the same as milligrams per 100 milliliters (mg/100 mL)
Example: What is the % (w/v) concentration of glucose in a patient with a blood glucose reading of 230 mg/dL? Note that 1 dL = 100 mL and that 230 mg = 0.23 g. Then,
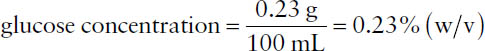
“Units” and Micrograms per Milligram
The concentrations for some drugs, e.g., antibiotics and vitamins, are expressed as “units” of activity or micrograms per milligram (mcg/mg) as determined by a standardized bioassay.
Example: A preparation of penicillin G sodium contains 2.2 mEq of sodium (atomic weight = 23, valence = 1) per 1 million units of penicillin. How many milligrams of sodium are contained in an IV infusion of 5 million units? The 5 million unit dose will contain 5 × 2.2 mEq = 11 mEq.
Weight of sodium = 23 mg/mEq × 11 mEq = 253 mg
Parts per Million and Parts per Billion
Very low concentrations often are expressed in terms of parts per million (ppm, or the number of parts of ingredient per million parts of mixture or solution) or parts per billion (ppb, or the number of parts of ingredient per billion parts of mixture or solution). Thus, ppm and ppb are special cases of ratio strength concentrations.
Example: Express 1:25,000 as parts per million.
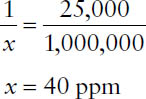
2-12. Dilutions and Concentrations
Simple Dilutions
In simple dilutions, a desired drug concentration is obtained by adding more solvent (diluent) to an existing solution or mixture. Mathematically, the key feature of this process is that the initial and final amounts of drug present remain unchanged. The amount of drug in any solution is proportional to the concentration times the quantity of the solution. Thus, taking the initial concentration as C1, the initial quantity of solution as Q1, the final concentration as C2, and the final quantity of solution as Q2, one has the relationship:
C1 × Q1 = C2 × Q2
When the values for any three of those variables are provided, the fourth variable can be calculated. (Because the equation can be rearranged to C1/C2 = Q2/Q1, it sometimes is referred to as an inverse proportionality.)
Example: How much water should be added to 250 mL of a solution of 0.2% (w/v) benzalkonium chloride to make a 0.05% (w/v) solution?
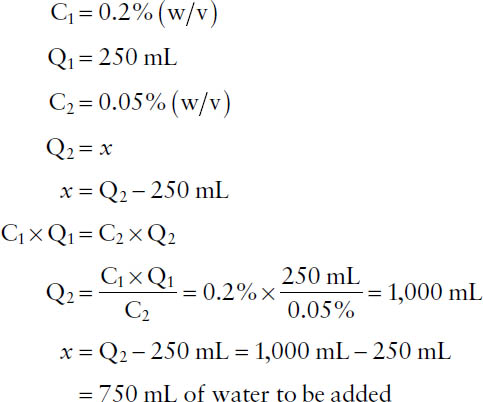
Alcohol Solutions
The preceding treatment of dilutions assumes that solution and solvent volumes are reasonably additive. For dilutions of concentrated ethyl alcohol in water, that is not the case, because a contraction in volume occurs on mixing. Consequently, you cannot extend the calculation to determine the exact volume of water to add to the initial alcohol solution. That is, the volume of water to be added cannot be obtained simply as Q2 – Q1. Rather, you can specify only that sufficient water be added to the initial concentrated alcohol solution (Q1) to reach the specified or calculated final volume (Q2) of the diluted alcohol solution.
Example:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


