This can be read as, “1000 mg is to 1 g as the unknown quantity is to 0.5 g.”

By cross-multiplying the top of each fraction (the numerators) by the bottom of the other fraction (the denominators), you get the following equation:

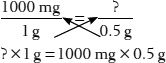
Now move all the numbers to the right side of the equation and leave only the ? on the left. You can do this by dividing both sides by 1 g and canceling common units. The calculations on the right then provide your answer:

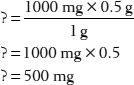
You can quickly solve problems by converting most calculations into this format. Just remember—always set up two proportions, one showing the information you’re given or what you know and the other putting the question mark in the appropriate place, depending on the information you’re looking for.

Units of Measure and Common Equivalents

A common type of calculation in pharmacy is converting between metric measurements (Table 2-1) and common equivalents that you typically encounter in the United States, such as pounds, inches, or quarts. The common system is also called the avoirdupois (pronounced AV-WA-DU-PWA) system, and it uses the units shown in Table 2-2.

Pharmacy uses a third set of measures, the apothecary system, which you may see occasionally, even though it is now largely unused (Table 2-3). In the apothecary system, remember that the grains are the same as grains in the avoirdupois system, but the ounces and pounds are different. While you will occasionally see drug doses expressed in grains and scruples, the Pharmacy Technician Certification Board (PTCB) examination does not include any items that test your knowledge of this antiquated system. The three drugs for which the apothecary system continues to be used most often are aspirin (a 325 mg aspirin tablet contains 5 grains of this drug), thyroid products, and phenobarbital.

Table 2-4 shows the mathematical relationships among the metric, apothecary, and avoirdupois systems.

These various units and systems give us a good chance to try using ratio and proportion to solve simple problems. Here are examples of questions you may encounter and problems you can use to test yourself. The answers to those problems not solved for you are shown at the end of this chapter.

  1. How many inches are in 4 feet?

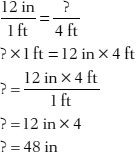
  2. How many milligrams are in 4 grams?

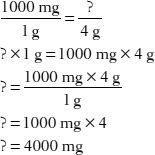
  3. How many milligrams are in 5 grains?

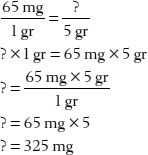
Note: As mentioned earlier in this chapter, a 5 gr aspirin tablet contains 325 mg. This is also the weight of a regular-dose acetaminophen (Tylenol) tablet or capsule.

  4. How many kilograms does a 154-pound person weigh?

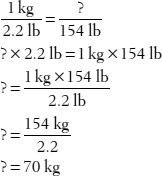
Did you know? Most pharmacokinetic calculations—those used by pharmacists to calculate drug dosages—are based on a 70 kg person. The equations are adjusted for the patient’s actual body mass as part of the calculation.

  5. How many milliliters are in 1 quart?

Tip: First convert the quart unit to ounces, then solve for milliliters!

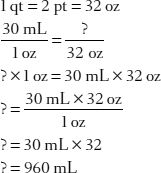
Now you complete some problems!

  6. How many grams are in 3 kilograms?

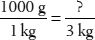
  7. How many milliliters are in 5 dL?

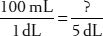
  8. How many inches are in 5 meters?

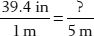
  9. If a patient weighs 22.4 kilograms, how many pounds is that?

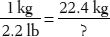
A new way to diet: Just give your weight in kilograms!

10. How many avoirdupois ounces are in 1 kg?

Tip: Use the 1 oz (avoirdupois) = 28.4 g conversion, but convert grams to kilograms by dividing by 1000.

For example: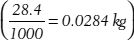

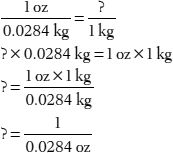
11. How many centimeters are in 6 inches?

12. How many milliliters are in 15 liters?

13. If an extra-strength tablet of Tylenol contains 500 mg of acetaminophen, how many grams are in 100 tablets? How many grams are in 1 tablet?

Hint: For the first part of this problem, the proportion would be .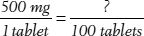

After you get an answer in milligrams, convert it to grams.

14. If a solution has 10 mg of drug per milliliter, how much drug is in 10 mL?

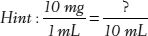
Percentage Calculations

While most medications are commercially available in ready-to-dispense form, pharmacists and pharmacy technicians sometimes make prescriptions from other ingredients through a process called compounding. This process will be described in more detail in Chapters 9 and 10.

Percentage calculations come into play during compounding when one substance (usually the drug) is dissolved or incorporated into a larger amount of a second substance. This is most often a solution in which a drug powder is dissolved in water or some other vehicle. The percentage then refers to the amount of drug (the solute) that is dispersed in the vehicle (the solvent). An example would be a solution of salt, or sodium chloride, dissolved in water.

Many of these products are prepared for injection into the veins, and many contain very powerful drugs. Because there is little room for error in these or any other pharmaceutical calculations, you need to be completely certain of the accuracy of your work. Always double or triple check your calculations or ask someone else to confirm them.

Fortunately, percentage calculations can be solved using the same ratio and proportion technique presented in the previous section, Units of Measure and Common Equivalents. All you have to remember is what “percentage” means: the amount of solute in milliliters or grams contained in 100 mL or 100 g of the final solution.

Weight-in-Volume Solutions (w/v)

If 5 g of dextrose (the chemical name for table sugar) is dissolved in water such that 100 mL of total solution is prepared (5 g per 100 mL), the result is a 5% solution of dextrose in water. Because this type of solution involves a certain weight of drug in a total volume of solution, it is sometimes called a weight-in-volume solution, and you will sometimes see the concentration expressed as 5% w/v to denote this relationship. But because this is the most common kind of solution, it is often understood that the percentage is w/v if nothing indicates otherwise.

Volume-in-Volume Solutions (v/v)

An example involving two liquids would be alcohol dissolved in water. A 70% ethanol solution in water is made up of 70 mL of ethanol (the kind of alcohol found in beer, wine, and liquor) mixed with enough water to make 100 mL of solution (70 mL per 100 mL). These types of solutions are sometimes called volume-in-volume solutions, and the percentage is then written as 70% v/v.

Weight-in-Weight Percentages (w/w)

When a drug is incorporated into another solid or semisolid product, such as a cream or ointment, the product is expressed as a weight-in-weight percentage. For example, 2 g of lidocaine mixed with enough of a compounding base to make 100 g of ointment (2 g per 100 g) would be a 2% w/w lidocaine ointment.

Let’s try a few problems using percentage calculations.

15. How many grams of dextrose are in 50 mL of a 5% w/v solution?

First, set up two common fractions that express the proportional relationships:

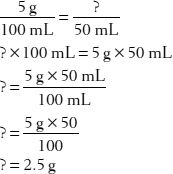
16. How many liters of a 5% dextrose solution contain 100 g of dextrose?

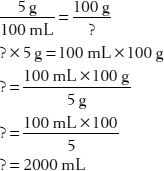
Now, convert 2000 mL to liters:

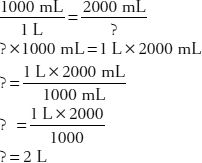
17. How many grams of lidocaine are in 75 g of a 2% w/w ointment?

18. How many milliliters of ethanol are in 35 mL of a 70% v/v ethanol solution?

19. How many grams of a 1% hydrocortisone cream contain 0.5 g of hydrocortisone?

20. How much sodium chloride is in 200 mL of a 0.9% solution?

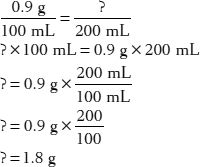
21. How much of a 70% v/v ethanol solution would contain 140 mL of ethanol?

Now try some on your own.

22. How many grams of dextrose would be needed to make 300 mL of a 5% dextrose solution?

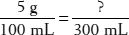
23. How many milliliters of ethanol are in 50 mL of a 50% v/v solution?

24. To prepare 150 g of a 2% w/w lidocaine ointment, how many grams of lidocaine would you need?

Ratio Strengths

Ratio strengths are another type of pharmaceutical calculation, and they are quite similar to percentage concentration problems. The amount of drug in a preparation is expressed as a ratio strength (for example, a 1:10 strength).

Similar to percentage calculations, ratio strength problems can be weight-in-volume, volume-in-volume, or weight-in-weight, depending on whether the preparation involves liquids or solids. This calculation most often involves a solution in which a drug powder is dissolved in water or some other vehicle. But it could also be a liquid dissolved in a liquid, as with alcohol in water, or a mixture of two solids, as with a drug in a cream or ointment. The percentage refers to the amount of drug (the solute) that is dispersed in the vehicle (the solvent).

With ratio strengths, you always assume that the solute is 1 part. Then you calculate how many parts of the final preparation contain that 1 part. For instance, in a 1:10 solution of sodium chloride, there is 1 part of sodium chloride in 10 parts of solution. This is basically the opposite of a percentage calculation where you are calculating the amount of solute present in 100 g or 100 mL of final product.

Here are some examples of ratio strength problems.

25. What is the ratio strength (w/v) of a solution with 2 g of drug in 50 mL of solution?

First, set up two common fractions that express the proportional relationships:

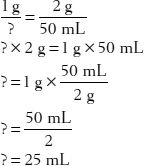
Therefore, the ratio strength is expressed as 1:25.

26. How many liters of a 1:20 dextrose solution contain 100 g of dextrose?

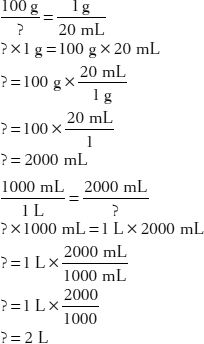
27. How many grams of lidocaine are in 75 g of a 1:50 w/w ointment?

28. How many milliliters of ethanol are in 35 mL of a 1:2 v/v ethanol solution?

29. How many grams of a 1:100 hydrocortisone cream contain 0.5 g of hydrocortisone?

30. How much sodium chloride is in 200 mL of a 1:111 solution?

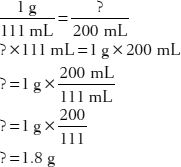
31. How much of a 1:1.43 v/v ethanol solution would contain 140 mL of ethanol?

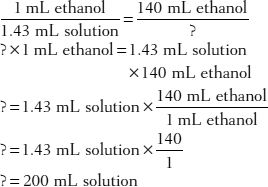
Here are some problems for you to try.

32. How many grams of dexamethasone are in 75 g of a 1:100 cream?

33. How many liters of a 1:2 alcohol solution contain 4 L of alcohol?

34. How many grams of dextrose are in 300 mL of a 1:20 solution?

Temperature Conversion

Although Americans are more familiar with Fahrenheit temperatures, most medical temperature measurements are taken using the Centigrade or Celsius system. As a result, pharmacy technicians are occasionally called on to convert between the two systems.

The Celsius scale is based on the freezing and boiling points of water, which are denoted as 0°C and 100°C. These two points are equivalent to 32°F and 212°F. To convert between the two systems, simply use the following equation:

9(°C) = 5(°F)–160

Let’s use this equation to solve some problems.

35. Convert 39°F to °C.

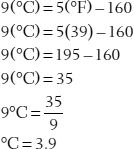
36. Convert 80°C to °F.

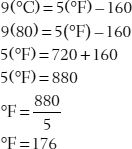
Now try some problems on your own.

37. Convert 98.6°F (normal body temperature) to °C.

38. Convert 20°C to °F.

Household Equivalents

In the community and ambulatory pharmacy settings, patients need to use common household measures to administer liquid medications. Table 2-5 provides conversions between metric quantities and household measurements. Let’s use the conversions to calculate drug dosages.

Stay updated, free articles. Join our Telegram channel

Join