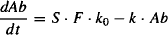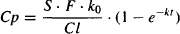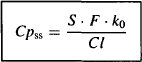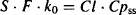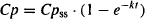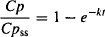11.2.1 Basic Equation
The starting point for the development of the basic equation is to consider how the amount of drug in the body changes with time:
rate of change of the amount of drug in the body = rate of inputs − rate of outputs
where S is the salt factor, F the bioavailability, and k0 the constant rate of drug administration. Equation (11.1) is integrated from zero to infinity:
(11.2) 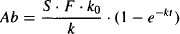
with Cp = Ab/Vd,
(11.3) 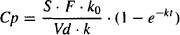
and with Cl = Vd · k,
Analysis of the Equation
- Recall (see Appendix A) that 1 – e−kt is the growth factor that starts at zero when t = 0 and grows to 1 at infinity.
- Thus, plasma concentrations start at zero and grow to the value of S · F · k0/Cl at infinity.
- The speed of growth is determined by the value of k (t1/2).
- The equation allows the plasma concentration to be estimated at any time during zero-order drug input.
- The shape of the plasma concentration–time profile corresponding to equation (11.4) is shown in Figure 11.2.
FIGURE 11.2 Plasma concentration–time profile during an intravenous infusion. When the plasma concentration remains constant, steady state has been achieved. The plasma concentration at steady-state plasma concentration is Cpss. Note that the unit of time is the elimination half-life.
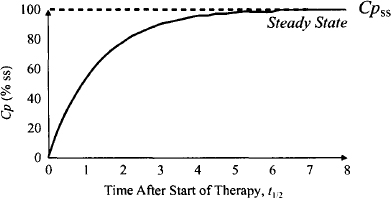
Note in Figure 11.2 that after the start of the infusion, the drug accumulates in the body and the plasma concentration increases. The rate of increase in the plasma concentration and the accumulation become less and less as therapy continues. Eventually, the plasma concentration becomes constant and drug accumulation ceases. The latter period is known as a steady-state and the corresponding plasma concentration is referred to as the steady-state plasma concentration (Cpss). It can be concluded that during a constant intravenous infusion, drug accumulation is a self-limiting process that eventually stops at steady state.
11.2.2 Application of the Basic Equation
The basic equation (11.4) enables the plasma concentration to be calculated at any time during continuous zero drug input (e.g., from an infusion or an oral preparation that delivers drug at a constant continuous rate).
Example 11.1 A drug (S = 1, Cl = 2 L/h, Vd = 50L) is administered as an intravenous infusion at a rate of 10 mg/h. Calculate the plasma concentration 4 h into the infusion.
Solution Cl = 21/h, Vd = 50 L, k = Cl/Vd = 2/50 = 0.04h−1, and t1/2 = 0.693/k = 17.3h.
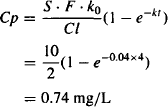
11.2.3 Simulation Exercise: Part 1
Open the model “Intravenous Infusion Model” at the link
http://www.uri.edu/pharmacy/faculty/rosenbaum/basicmodels.html#chapter11a
The default model parameters are S = 1, F = 1, infusion rate = 10 mg/h, Cl = 5 L/h, and Vd = 20L
TABLE SE11.1 Infusion Rates and the Corresponding Cpss
| Simulation | Infusion Rate | Cpss |
| 1 | 5 mg/h | |
| 2 | 10 mg/h | |
| 3 | 20 mg/h | |
| 4 | 6 mg/L |
11.3 STEADY-STATE PLASMA CONCENTRATION
At steady state, the plasma concentration becomes constant and independent of time (Figure 11.2). The value of the steady-state plasma concentration is a very important focus of drug treatment. Usually, it is desirable to have a steady-state plasma concentration in the middle of the therapeutic range. To plan this, it is necessary to understand the factors that control the steady-state plasma concentration.
11.3.1 Equation for Steady-State Plasma Concentrations
There are two ways to derive the equation for the steady-state plasma concentration.
Derivation 1 Before steady state, the plasma concentration is given by equation (11.4). As t increases, the exponential growth function, 1 – e−kt, tends to 1, and Cp tends to Cpss:
The box around equation (11.5) signifies that it is an important equation, as we demonstrate in Section 11.3.4.
Derivation 2 At steady state the plasma concentration is constant. Thus, the rate of drug administration must equal the rate of drug elimination:
Equation (11.6) can be rearranged to yield equation (11.5).
11.3.2 Application of the Equation
We look next at two examples that illustrate application of the steady-state plasma concentration equation.
Example 11.2 The same drug as that described in Example 11.1 is administered as an intravenous infusion at a rate of 10 mg/h. Calculate the steady-state plasma concentration. Recall that Cl = 2 L/h, Vd = 50 L, S = 1, k = Cl/Vd = 2/50 = 0.04h−1, and t1/2 = 0.693/k = 17.3 h.
Solution
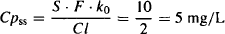
Example 11.3 A drug (S = 0.9, F = 0.94, Cl = 1.44 L/h, Vd = 0.65 L/kg) has a therapeutic range of 10 to 20 mg/L. It is formulated into an oral elementary osmotic pump, which delivers the drug at a constant rate of 12 mg/h. The preparation is designed for administration every 12 h and is available in units of 250, 300, and 400 mg. Determine a suitable dose to achieve a steady-state plasma concentration of 15 mg/L in a 60-kg woman.
Solution
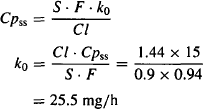
The unit dosage forms are designed to administer the dose at a constant rate over a 12-h period. If a rate of 25.5 mg/h is required, the unit dose must contain 25.5 × 12 = 306 mg. Thus, the 300-mg unit should be given twice daily.
11.3.3 Basic Formula Revisited
The expression for the steady-state plasma concentration given in equation (11.5) may be substituted into the basic equation for the plasma concentration before steady state, as given in equation (11.4):
This equation shows that the plasma concentration grows from zero at time zero (1 – e−kt = 0) to the steady-state plasma concentration at time infinity (1 – e−kt = 1).
11.3.4 Factors Controlling Steady-State Plasma Concentration
Equation (11.5), which shows the factors that control the steady-state plasma concentration, is reproduced below.
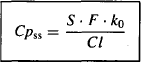
The box surrounding it designates that it is an important equation. This equation, probably the most important and useful of all pharmacokinetic equations, shows that the terminal plasma concentration achieved by a given rate of drug administration is dependent only on the effective rate of drug administration and clearance. It also provides insight into when it may be prudent to modify the usual rate of drug administration.
Specifically, the equation shows the following points:
11.3.5 Time to Steady State
The basic equation for the plasma concentration during constant continuous drug administration is given by equation (11.7), which can be rearranged as
The left-hand side of equation (11.8) is the fraction of steady state achieved at any time. Thus, 1 – e−kt represents the fraction of steady state achieved at any time. Recall (see Appendix A) that the function 1 – e−kt
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree