“Preparation” is frequently a solution but may be an ointment, a suppository, a powder mixture, and so on.

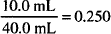
Percent concentration is defined as the number of parts of solute in 100 units of solution. Concentration expressed as a decimal may be converted to percent by multiplying by 100:
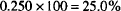
This concentration may be written 25.0% by volume or 25.0% volume in volume or 25.0% v/v to indicate that both the solute and solution were measured by volume.
If 12.0 mL of peppermint oil were dissolved in sufficient alcohol to make 80.0 mL of solution, what would be the concentration of peppermint oil in this solution expressed as

Solutions.
CALCULATIONS
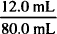 mL = 0.150 v/v
mL = 0.150 v/v

Solution. 0.05% v/v
CALCULATION
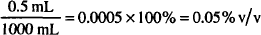

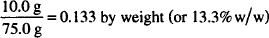
Note: In a preparation in which all concentrations are w/w, the sum of all contributions must be 100%.
If 12.0 g of lanolin are combined with 2.0 g of white wax and 16.0 g of petrolatum to make an ointment, what is the percentage concentration of lanolin in the ointment?

Solution. 40.0% w/w
CALCULATIONS
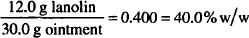


Solution. 45% w/w
CALCULATIONS
300 mL water = 300 g
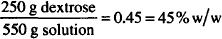


Solution. 5.8% w/w
CALCULATIONS
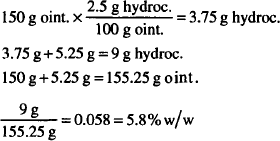

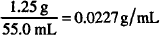
Commonly, this concentration will be stated as a percent, w/v. The appendage “w/v” tells us that the solute is expressed in grams and that the quantity of solution is determined by volume in milliliters. These implied units must not be neglected in calculations.
By multiplying grams per milliliter by 100, we obtain the number of grams in 100 mL, which defines percent w/v:

If 5.75 g of boric acid are dissolved in sufficient alcohol to make a total volume of 120 mL, what is the strength of boric acid in the solution in

Solutions.
CALCULATIONS
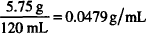


Solutions.
CALCULATIONS
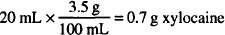
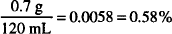
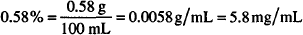

In each case, determine the percent concentration of glycerin and indicate whether w/w, v/v, or w/v:

Solutions.
CALCULATIONS
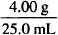 = 0.160 g/mL = 16.0% w/v
= 0.160 g/mL = 16.0% w/v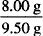 = 0.842 w/w = 84.2% w/w
= 0.842 w/w = 84.2% w/w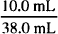 = 0.263 v/v = 26.3% v/v
= 0.263 v/v = 26.3% v/v
Default Rules if Percentage Type is not Indicated
Let us look at an example. Say that you make up a solution of peppermint oil in alcohol by dissolving 2.0 mL of oil in enough alcohol to make 100 mL of solution. The concentration is
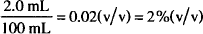
If your product is labeled “Peppermint Oil Solution, 2.0%,” the default rules apply. Since both peppermint oil and alcohol are liquids, it is assumed that both will be measured by volume. Therefore, “2.0%” means 2.0% v/v in this case, so that your label describes the product accurately.
However, if you were to make up a solution by dissolving 2.0 g of peppermint oil in sufficient alcohol to make up 100 mL of solution? Then “2.0%” would not accurately describe the product. It would have to be labeled 2.0% w/v.
If 4.0 g of peppermint oil are dissolved in 96.0 g of alcohol, how would you describe the concentration of peppermint oil in this solution?

Solution. 4% w/w
CALCULATIONS
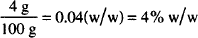
Peppermint oil and alcohol are liquids and would normally be measured by volume. But in this example, the solution was prepared by weight. The “percent w/w” designation transmits this information. If the concentration were written “4.0%,” the default rules would apply and we would be (incorrectly) led to believe that the solution was prepared by volume.


Solution. 1% w/v
CALCULATIONS
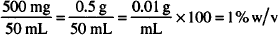


Solutions.

Prescriptions with Ingredients Listed as Percentage
 | Zinc sulfate (a solid) | 1/2% |
| Aq. pur. qs ad | 60.0 mL |
In this prescription the drag content is specified on the basis of concentration. We must calculate the quantities needed to prepare this solution. Zinc sulfate is a solid and the final product is a liquid, so the concentration is taken to be w/v. Thus the zinc sulfate concentration is 0.5 g/100 mL or 0.005 g/mL.
The most direct way of calculating the quantity of zinc sulfate is to rearrange the definition of concentration:
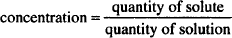
to quantity of solute = concentration × quantity of solution
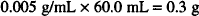
Dissolve 0.3 g of zinc sulfate in sufficient purified water to make 60 mL.
Now consider this prescription:
 | Eucalyptus oil | 2.5% v/v |
| Mineral oil | qs ad 30.0 |
What quantities should be used for this prescription?

Solution. Eucalyptus oil: 0.75 mL
Mineral oil: sufficient to make 30.0 mL of solution
CALCULATION
30.0 mL × 0.025 = 0.75 mL

| 14. |  | Sulfur 10.0% |
| Benzoic acid 1.5% | ||
| Petrolatum qs ad 30.0 | ||
| Ft ung |
All ingredients are solids. What quantity of each should be used to make this ointment? (Remember that all three ingredients must be weighed.)

| Solution. | Sulfur: 3.00 g |
| Benzoic acid: 0.450 g | |
| Petrolatum: 26.6 g |
CALCULATIONS
All ingredients are solids. According to the default rules, we treat the concentrations as percent w/w:
Sulfur: 30.0 g × 0.1 = 3.00 g
Benzoic acid: 30.0 g × 0.015 = 0.450 g
The sum of all percentages must be 100%. This is necessarily true only in a preparation in which all concentrations are w/w. From the prescription, we can see that 88.5% of the ointment is petrolatum.
Petrolatum: 30.0 g × 0.885 = 26.6 g
To check, verify that the sum of all contributions is 30.0 g.


How much boric acid (a solid) and camphor water (a liquid) are needed for this prescription? (Here is a situation in which two concentration types appear in the same solution. The boric acid must be considered on a w/v basis, whereas the camphor water is handled on a v/v basis. Treat each substance separately in doing your calculations.)

| Solution. | Boric acid: 300 mg |
| Camphor water: 5.25 mL |
CALCULATIONS
Boric acid: 15.0 mL × 0.02 g/mL = 0.300 g
Camphor water: 15.0 mL × 0.35 = 5.25 mL


Solutions.
CALCULATIONS
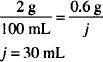
Alternatively,
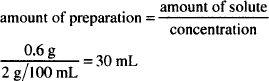


Solution. 2.22 L
CALCULATIONS

Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


