(15.1)
If the investigator is concerned about some kind of departure from the model in (15.1), the center points can provide a test for such a departure, although it provides little information as to the exact type of departure (del Castillo 2007, pp. 411–412).
As the number of factors to be studied increases, full factorial designs quickly become too costly. If we are willing to assume that higher order interactions are negligible, then one should consider fractional factorial designs. Negligible higher order interactions are associated with a certain degree of smoothness on the underlying response surface. If we believe that the underlying process is not very volatile as we change the factors across the experimental region, then the assumption of negligible higher order interactions may be reasonable. Fractional factorial designs are often certain fractions of a 2 k factorial design. They have the design form 2 k–p , where k is the number of factors and p is associated with the particular fraction of the 2 k design. For example, a 25-1 design denotes a half-replicate of a 25 design, while 26-2 denotes a one-fourth replicate of a 26 design.
For fractional factorial designs, some interaction terms are confounded (or aliased) with possibly first order or other interaction terms. This means that certain interaction terms cannot be estimated apart from other terms. If (negligible) higher order interactions terms are confounded with first order or lower order interaction terms, then we may still be able to make practical inferences from a fractional factorial design analysis. Fractional factorial designs can be categorized into how well they can “resolve” factor effects. These categories are called design resolution categories. For a resolution III design, no main effects (first order terms) are confounded with any other main effect, but main effects are aliased with two-factor interactions and two-factor interactions are aliased with each other. For a resolution IV design, no main effect is aliased with any other main effect or with any two-factor interaction, but two-factor interactions are aliased with each other. For a resolution V design, no main effect or two-factor interaction is aliased with any other main effect or two-factor interaction, but two-factor interactions are aliased with three-factor interactions. Resolution III and IV designs are particularly good for factor screening as they efficiently provide useful information about main effects and some information about two-factor interactions (Montgomery 2009, chapter 13).
Recently, a special class of screening design has gathered some popularity. It is called a “definitive screening design”. It requires only twice the number of runs as there are factors in the experiment. The analysis of these designs is straightforward if only main effects or main and pure-quadratic effects are active. The analysis becomes more challenging if both two-factor interactions and pure-quadratic effects are active because these may be correlated (partially aliased) (Jones and Nachtsheim 2011). If a factor’s effect is strongly curvilinear, a fractional factorial design may miss this effect and screen out that factor. If there are more than six factors, but three or fewer are active, then the definitive screening design is capable of estimating a full quadratic response surface model in those few active factors. In this case, a follow-up experiment may not be needed for a response surface analysis.
15.2.2 Response Surfaces: Experimental Design and Optimization
Factorial and fractional factorial designs are useful for factor screening so that experimenters can identify the key factors that affect their process. It may be the case the results of a factorial or a fractional factorial design produce sufficient process improvement that the pharmaceutical scientist or chemical engineer will decide to terminate any further process improvement experiments. However, it is important to understand that a response surface follow up experiment may not only produce further process improvement, but it will also produce further process understanding by way of the response surface. If a process requires modification of factor settings (e.g. due to an uncontrollable change in another factor) it may not be clear how to make such a change without a response surface, particularly if the only experimental information available is from a fractional factorial design.
The results of the factor screening experiments may provide some indication that the process optimum may be within the region of the screening experiment. This could be the case, for example, if the response from center-point runs are better than all of the responses at the factorial design points. However, it is probably more likely that the results of the screening design point towards a process optimum that is towards the edge, or outside of, the factor screening experimental region. If this is the case, and if the results of the screening experiment provide no credible evidence of response surface curvature within the original region, then the experimenter should consider the method of “steepest ascent/descent” for moving further towards the process optimum. The classical method of steepest ascent/descent uses a linear surface approximation to move further towards the process optimum. Often, the original screening design may provide sufficient experimental points to support a linear surface. Clearly, statistical and practically significant factor interactions and/or a significant test for curvature indicates that a second-order response surface model needs to be built as the linear surface is not an adequate approximation. The method of steepest ascent/descent is a form of a “ridge analysis” (in this case for a linear surface), to be reviewed briefly below. See Myers et al. (2009, chapter 5) for further details on steepest ascent.
Special experimental designs exist for developing second-order response surface models. If it appears from the screening design that the process optimum may well be within the original experimental region, then a central composite design may be able to be developed by building upon some of the original screening design points (Myers et al. 2009, pp. 192–193). The Box–Behnken design (Box and Behnken 1960) is also an efficient design for building second-order response surfaces.
Once a second-order response surface model is developed, analytical and graphical techniques exist for exploring the surface to determine the nature of the “optimum”. The basic form for the second-order response surface is
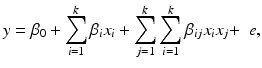
where y is the response variable, x 1, …, x k are the factors. It is often useful to express the equation in (15.2) in the vector–matrix form as
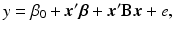
where 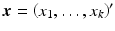 ,
, 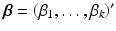 , and B is a symmetric matrix whose ith diagonal element is β ii and whose (i, j)th-off diagonal element is
, and B is a symmetric matrix whose ith diagonal element is β ii and whose (i, j)th-off diagonal element is 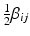 . The form in (15.3) is useful in that the matrix B is helpful in determining shape characteristics of the quadratic surface. If B is positive definite (i.e. all eigenvalues are positive), then the surface is convex (upward), while if B is negative definite (i.e. all eigenvalues are negative), then the surface is concave (downward). If B is positive or negative definite, then the surface associated with (15.3) has a stationary point that is a global minimum or maximum, respectively. If, however, some of the eigenvalues of B change sign, then the surface in (15.3) is that of a “saddle surface”, which has a stationary point, but no global optimum (maximum or minimum). The stationary point,
. The form in (15.3) is useful in that the matrix B is helpful in determining shape characteristics of the quadratic surface. If B is positive definite (i.e. all eigenvalues are positive), then the surface is convex (upward), while if B is negative definite (i.e. all eigenvalues are negative), then the surface is concave (downward). If B is positive or negative definite, then the surface associated with (15.3) has a stationary point that is a global minimum or maximum, respectively. If, however, some of the eigenvalues of B change sign, then the surface in (15.3) is that of a “saddle surface”, which has a stationary point, but no global optimum (maximum or minimum). The stationary point, 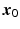 , is that point at which the gradient vector of the response surface is stationary (i.e. all elements of the gradient vector are zero). It follows then that
, is that point at which the gradient vector of the response surface is stationary (i.e. all elements of the gradient vector are zero). It follows then that
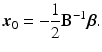
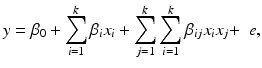
(15.2)
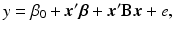
(15.3)
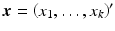 ,
, 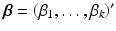 , and B is a symmetric matrix whose ith diagonal element is β ii and whose (i, j)th-off diagonal element is
, and B is a symmetric matrix whose ith diagonal element is β ii and whose (i, j)th-off diagonal element is 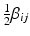 . The form in (15.3) is useful in that the matrix B is helpful in determining shape characteristics of the quadratic surface. If B is positive definite (i.e. all eigenvalues are positive), then the surface is convex (upward), while if B is negative definite (i.e. all eigenvalues are negative), then the surface is concave (downward). If B is positive or negative definite, then the surface associated with (15.3) has a stationary point that is a global minimum or maximum, respectively. If, however, some of the eigenvalues of B change sign, then the surface in (15.3) is that of a “saddle surface”, which has a stationary point, but no global optimum (maximum or minimum). The stationary point,
. The form in (15.3) is useful in that the matrix B is helpful in determining shape characteristics of the quadratic surface. If B is positive definite (i.e. all eigenvalues are positive), then the surface is convex (upward), while if B is negative definite (i.e. all eigenvalues are negative), then the surface is concave (downward). If B is positive or negative definite, then the surface associated with (15.3) has a stationary point that is a global minimum or maximum, respectively. If, however, some of the eigenvalues of B change sign, then the surface in (15.3) is that of a “saddle surface”, which has a stationary point, but no global optimum (maximum or minimum). The stationary point, 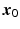 , is that point at which the gradient vector of the response surface is stationary (i.e. all elements of the gradient vector are zero). It follows then that
, is that point at which the gradient vector of the response surface is stationary (i.e. all elements of the gradient vector are zero). It follows then that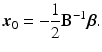
Further insight into the nature of a quadratic response surface can be assessed by doing a “canonical analysis” (Myers et al. 2009, chapter 6). A canonical analysis invokes a coordinate transformation that replaces the equation in (15.2) with
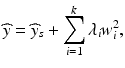
where ŷ s is the predicted response at the estimated stationary point, 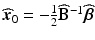 , and λ 1, …, λ k are the eigenvalues of
, and λ 1, …, λ k are the eigenvalues of 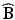 . The variables, w 1, …, w k , are known as the canonical variables, where
. The variables, w 1, …, w k , are known as the canonical variables, where 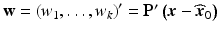 and P is such that
and P is such that 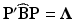 and
and 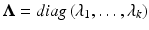 . Here, P is a
. Here, P is a 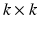 matrix of normalized eigenvectors associated with
matrix of normalized eigenvectors associated with 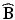 .
.
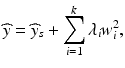
(15.4)
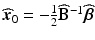 , and λ 1, …, λ k are the eigenvalues of
, and λ 1, …, λ k are the eigenvalues of 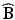 . The variables, w 1, …, w k , are known as the canonical variables, where
. The variables, w 1, …, w k , are known as the canonical variables, where 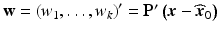 and P is such that
and P is such that 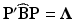 and
and 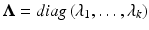 . Here, P is a
. Here, P is a 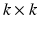 matrix of normalized eigenvectors associated with
matrix of normalized eigenvectors associated with 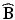 .
.One can see from (15.4) that if |λ i | is small, then moving in the direction vector given by (0,.., 0, λ i , 0, …, 0)′ (in the w-space) will result in little change from the stationary point. Such movements can be useful if, for example, process cost can be reduced for conditions somewhat away from the stationary point, but on or close to the line intersecting 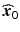 along the (0,.., 0, λ i , 0, …, 0)′ direction in the w-space.
along the (0,.., 0, λ i , 0, …, 0)′ direction in the w-space.
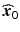 along the (0,.., 0, λ i , 0, …, 0)′ direction in the w-space.
along the (0,.., 0, λ i , 0, …, 0)′ direction in the w-space.However, the response surface shape may indicate that a global optimum is not within the regions covered by experimentation thus far. Or, it may be that operation at the estimated stationary point, 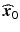 , is considered too costly. In such cases, it may be useful to conduct a “ridge analysis”. This is a situation where we want to do constrained optimization, staying basically within the experimental region. For a classical ridge analysis (Hoerl 1964), we optimize the quadratic response surface on spheres (of varying radii) centered at the origin of the response surface design region. In fact, one can consider ridge analysis to be the second-order response surface analogue of the steepest ascent/descent method for linear response surfaces. Draper (1963) provides an algorithmic procedure for producing a ridge analysis for estimated quadratic response surfaces. Peterson (1993) generalizes the ridge analysis approach to account for the model parameter uncertainty and to also make it apply to a wider class of models which are only linear in the model parameters, e.g. many mixture experiment models (Cornell 2002).
, is considered too costly. In such cases, it may be useful to conduct a “ridge analysis”. This is a situation where we want to do constrained optimization, staying basically within the experimental region. For a classical ridge analysis (Hoerl 1964), we optimize the quadratic response surface on spheres (of varying radii) centered at the origin of the response surface design region. In fact, one can consider ridge analysis to be the second-order response surface analogue of the steepest ascent/descent method for linear response surfaces. Draper (1963) provides an algorithmic procedure for producing a ridge analysis for estimated quadratic response surfaces. Peterson (1993) generalizes the ridge analysis approach to account for the model parameter uncertainty and to also make it apply to a wider class of models which are only linear in the model parameters, e.g. many mixture experiment models (Cornell 2002).
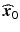 , is considered too costly. In such cases, it may be useful to conduct a “ridge analysis”. This is a situation where we want to do constrained optimization, staying basically within the experimental region. For a classical ridge analysis (Hoerl 1964), we optimize the quadratic response surface on spheres (of varying radii) centered at the origin of the response surface design region. In fact, one can consider ridge analysis to be the second-order response surface analogue of the steepest ascent/descent method for linear response surfaces. Draper (1963) provides an algorithmic procedure for producing a ridge analysis for estimated quadratic response surfaces. Peterson (1993) generalizes the ridge analysis approach to account for the model parameter uncertainty and to also make it apply to a wider class of models which are only linear in the model parameters, e.g. many mixture experiment models (Cornell 2002).
, is considered too costly. In such cases, it may be useful to conduct a “ridge analysis”. This is a situation where we want to do constrained optimization, staying basically within the experimental region. For a classical ridge analysis (Hoerl 1964), we optimize the quadratic response surface on spheres (of varying radii) centered at the origin of the response surface design region. In fact, one can consider ridge analysis to be the second-order response surface analogue of the steepest ascent/descent method for linear response surfaces. Draper (1963) provides an algorithmic procedure for producing a ridge analysis for estimated quadratic response surfaces. Peterson (1993) generalizes the ridge analysis approach to account for the model parameter uncertainty and to also make it apply to a wider class of models which are only linear in the model parameters, e.g. many mixture experiment models (Cornell 2002).15.2.3 Ruggedness and Robustness
Once an analytical assay, or other type of process, has been optimized, one may want to assess the sensitivity of the assay or process to minor departures from the set process conditions. Here, we call this analysis a “ruggedness” assessment. Some of these conditions may involve factors for which the process is known to be sensitive, while other conditions may involve factors that (through testing or process knowledge) are known to be less influential. In a ruggedness assessment, the experimenter has to keep in mind how much control is possible for each factor. If one has tight control on all of the sensitive factors, then the process may indeed be rugged against deviations that commonly occur in manufacturing or in practical use (e.g. as with a validation assay). Ruggedness evaluations are often done on important assays that are used quite frequently.
Much of the classical literature on ruggedness evaluations for assays involve performing screening designs with many factors over carefully chosen (typically small) ranges. See, for example, Vander Heyden et al. (2001). The purpose of such an experiment is to see if any factor effects are statistically (and practically) significant. However, such experiments are typically not designed to have pre-specified power to detect certain effects with high probability. Furthermore, a typical factorial analysis of variance does not capture the probability that future responses from a process over this ruggedness experimental region will be within specifications. To address this issue, Peterson and Yahyah (2009) apply a Bayesian predictive approach to quantify the maximum and minimum probabilities that a future response will meet specifications within the ruggedness experimental region. If the maximum probability is too small, the process is not considered rugged. However, if the minimum probability is sufficiently large, then the process is considered rugged.
This problem of process sensitivity to certain factors can sometimes be addressed by moving the process set conditions to a point that, while sub-optimal, produces a process that is more robust to minor deviations from the set point. This can sometimes be achieved by exploiting factor interactions, or from an analysis of a response surface. In some situations, however, the process is sensitive to factors which are noisy. This may be particularly true in manufacturing where process factors cannot be controlled as accurately as on the laboratory scale.
When a process will be ultimately subject to noisy factors (often called noise variables), a robustness analysis can be employed known as “robust parameter design” (Myers et al. 2009, chapter 10). Robust parameter design has found productive applications in industries involving automobile, processed food, detergent, and computer chip manufacturing. However, it has to date, not been widely employed in the pharmaceutical industry, although applications to the pharmaceutical industry are starting to appear in the manufacturing literature (Cho and Shin 2012; Shin et al. 2014).
The basic idea behind robust parameter design is that the process at manufacturing scale has both noise factors and controllable factors. For example, noise factors might be temperature (deviation from set point) and moisture, while controllable factors might be processing time and a set point associated with temperature. If any of the noise variables interact with the one or more of the controllable factors, then it may be possible to reduce the transmission of variation produced by the noise variables. This may result in a reduction in variation about a process target, which in turn will increase the probability of meeting specification for that process. There is quite a large literature on statistical methods associated with robust parameter design involving a univariate process response. (See Myers et al. 2009, chapter 10 for references.) However, there are fewer articles on robust parameter design method for multiple response processes (e.g. Miró-Quesada et al. 2004). Miró-Quesada et al. (2004) introduce a Bayesian predictive approach that is widely applicable to both single and multiple response robust parameter design problems.
15.2.4 Process Capability
During or directly following process optimization, the experimenter should also consider some aspect of process capability analysis. Such an analysis involves assessing the distribution of the process response over its specification interval (or region) and the probability of meeting specifications. Assessment of process capability involves a joint assessment of both the process mean and variance, as well as the variation of the process responses about the quality target, which in turn is related to the probability of meeting specifications. Further process capability should also be assessed during pilot plant and manufacturing as part of the process monitoring activities. This is because the distribution of process responses may involve previously unforeseen temporal effects associated with sequential trends, the day of the week, etc. Process capability is clearly important because a process may be optimized, but it may not be “capable”, i.e. it may have an unacceptable probability of meeting specifications.
Process capability indices have become popular as a way to succinctly quantify process capability. The C p index has the form
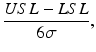 where USL = “upper specification limit”, LSL = “lower specification limit”, and
where USL = “upper specification limit”, LSL = “lower specification limit”, and 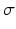 equals the process standard deviation. The C p index is estimated by substituting the estimated standard deviation,
equals the process standard deviation. The C p index is estimated by substituting the estimated standard deviation, 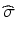 , for σ. As one can clearly see, the larger the C p index, the better is the process capability. However, the C p index does not take into account where the process mean is located relative the specification limits. A more sensitive process capability index is denoted as C pk which has the form
, for σ. As one can clearly see, the larger the C p index, the better is the process capability. However, the C p index does not take into account where the process mean is located relative the specification limits. A more sensitive process capability index is denoted as C pk which has the form
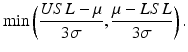 The C pk index is estimated by substituting the estimates for
The C pk index is estimated by substituting the estimates for 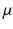 and
and 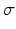 for their respective population parameters appearing in the C pk definition. The magnitude of C p relative to C pk is a measure of how off center a process is relative to its target.
for their respective population parameters appearing in the C pk definition. The magnitude of C p relative to C pk is a measure of how off center a process is relative to its target.
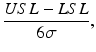
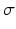 equals the process standard deviation. The C p index is estimated by substituting the estimated standard deviation,
equals the process standard deviation. The C p index is estimated by substituting the estimated standard deviation, 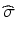 , for σ. As one can clearly see, the larger the C p index, the better is the process capability. However, the C p index does not take into account where the process mean is located relative the specification limits. A more sensitive process capability index is denoted as C pk which has the form
, for σ. As one can clearly see, the larger the C p index, the better is the process capability. However, the C p index does not take into account where the process mean is located relative the specification limits. A more sensitive process capability index is denoted as C pk which has the form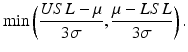
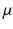 and
and 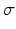 for their respective population parameters appearing in the C pk definition. The magnitude of C p relative to C pk is a measure of how off center a process is relative to its target.
for their respective population parameters appearing in the C pk definition. The magnitude of C p relative to C pk is a measure of how off center a process is relative to its target.Statistical inference relative to process capability indices require critical care. Such index estimates may have rather wide sampling variability. In addition, the process capability index can be misleading if the process is not in control (i.e. stable and predictable). It is hoped that before or during the process optimization phase that a process can be brought into control. However, validation of such control may need to be confirmed during the actual running of the process over time using statistical process monitoring techniques (Montgomery 2009, p. 364). In addition, process capability indices have in the past received criticism for trying to represent a multifaceted idea (process capability) as one single number (Nelson 1992; Kotz and Johnson 2002). While this criticism has some merit (and is applicable to any other single statistic), it is only valid if such indices are reported to the exclusion of other aspects of the distribution of process responses.
15.2.5 Measurement System Capability
Measurement capability is an important aspect of any quality system. If measurements are poor (e.g. very noisy and/or biased) process improvement may be slow and difficult. As such, it is important to be able to assess the capability of a measurement system, and improve it if necessary. This section will review concepts and methods for measurement system capability assessment and improvement.
Two important concepts in measurement capability analysis are “repeatability” and “reproducibility”. Repeatability is the variation associated with repeated measures on the same unit under identical conditions, while reproducibility is the variation associated when units are measures under different natural process conditions, such as different operators, time periods, etc. A measurement system with good capability is able to easily distinguish between good and bad units.
A simple model for measurement systems analysis (MSA) is
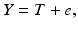 where Y is the observed measurement on the system, T is the true value of the system response (for a single unit, e.g. a batch or tablet), and e is the error difference. (It is assumed here that Y, T and e are stochastically independent.) In MSA the total variance of this system is typically represented by
where Y is the observed measurement on the system, T is the true value of the system response (for a single unit, e.g. a batch or tablet), and e is the error difference. (It is assumed here that Y, T and e are stochastically independent.) In MSA the total variance of this system is typically represented by
 where
where 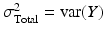 ,
, 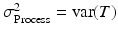 , and
, and 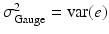 . Clearly, accurate measuring devices are associated with a small “gauge” variance. It is also possible to (additively) decompose the gauge variance into two natural variance components, σ Repeatability2 and σ Reproducibility2. Here, “reproducibility” is the variability due to different process conditions (e.g. different operators, time periods, or environments), while “repeatability” is the variation due to the gauge (i.e. measuring device) itself. The experiment used to measure the components of σ Gauge2 is typically called a “gauge R&R” study.
. Clearly, accurate measuring devices are associated with a small “gauge” variance. It is also possible to (additively) decompose the gauge variance into two natural variance components, σ Repeatability2 and σ Reproducibility2. Here, “reproducibility” is the variability due to different process conditions (e.g. different operators, time periods, or environments), while “repeatability” is the variation due to the gauge (i.e. measuring device) itself. The experiment used to measure the components of σ Gauge2 is typically called a “gauge R&R” study.
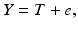

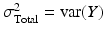 ,
, 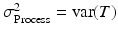 , and
, and 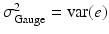 . Clearly, accurate measuring devices are associated with a small “gauge” variance. It is also possible to (additively) decompose the gauge variance into two natural variance components, σ Repeatability2 and σ Reproducibility2. Here, “reproducibility” is the variability due to different process conditions (e.g. different operators, time periods, or environments), while “repeatability” is the variation due to the gauge (i.e. measuring device) itself. The experiment used to measure the components of σ Gauge2 is typically called a “gauge R&R” study.
. Clearly, accurate measuring devices are associated with a small “gauge” variance. It is also possible to (additively) decompose the gauge variance into two natural variance components, σ Repeatability2 and σ Reproducibility2. Here, “reproducibility” is the variability due to different process conditions (e.g. different operators, time periods, or environments), while “repeatability” is the variation due to the gauge (i.e. measuring device) itself. The experiment used to measure the components of σ Gauge2 is typically called a “gauge R&R” study.The estimation of variance components associated with a gauge R&R study are applied not only to pharmaceutical manufacturing process, but also to important assays. If a process or assay shows unacceptable variation, a careful variance components analysis may help to uncover the key source (or sources) of variation responsible for poor process or assay performance.
15.2.6 Statistical Process Control
In pharmaceutical manufacturing or in routine assay utilization, such processes will tend to drift over time and will eventually fall out of a state of control. All CMC processes have some natural (noise) variation to which they are subject. If this source of underlying variation is natural and historically known, this is typically called “common cause” variation. Such variation is “stationary” in the sense that it is random and does not drift or change abruptly over time. A process that is in control will be subject only to common cause variation. However, other types of variation will eventually creep in and affect a process. These sources of variation are known as “special cause” variation. Typical sources of special cause variation are: machine error, operator error, or contaminated raw materials. Special cause variation is often large when compared to common cause variation. Special cause variation can take on many forms. For example, it may appear as a one-time large deviation or as a gradual trend that eventually pushes a process out of control. Statistical process control (SPC) is a methodology for timely detection of special cause variation and more generally for obtaining a better understanding of process variation, particularly with regard to temporal effects. See Chap. 20 for additional discussion on this and related topics.
As a practical matter, it is important to remember that SPC only provides detection of special cause variation. Operator or engineering action will be needed to eliminate these special causes of variation, so that the process can be brought back into a state of control. Identification of an assignable cause for the special cause variation may require further statistical analysis or experimentation (e.g. a variance components analysis).
An SPC chart is used to monitor a process so that efficient detection of special cause variation can be obtained. An SPC chart consists of a “center line” that represents the mean of the quality statistic being measured when the process is in a state of control. The quality statistic is typically not just one single measured process response but rather the average of a group of the same quality responses chosen within a close time frame. It is expected that the common cause variation will induce random variation of this statistic about the center line. The SPC chart also has upper and lower control limits. These two control limits are chosen (with respect to the amount of common cause variation) so that nearly all of the SPC statistic values over time will fall between them. If the statistic values being measured over time vary randomly about the center line and stay within the control limits, then the process is in state of control and no action is necessary. In fact, any action to try to improve a process that is subject only to common cause variation may only increase the variation of that process. If however the SPC statistic values start to fall outside of the control limits or behave in a systematic or nonrandom manner about the center line, then this suggests that the process is out of control.
SPC methodology involves a variety of statistical tools for developing a control chart to meet the needs of the process and the manufacturer. Specification of the control limits is one of the most important decisions to be made in creating a control chart. Such specification should be made relative to the distribution of the quality statistic being measured, e.g. the sample mean. If the quality statistic being measured is a sample mean, then it is common practice to place the control limits at an estimated “3 sigma” distance from the center line. Here, sigma refers to the standard deviation of the distribution of the sample mean, not the population of individual quality responses. Three-sigma control limits have historically performed well in practice for many industries.
Another critical choice in control chart development involves collection of data in “rational subgroups”. The strategy for the selection of rational subgroups should be such that data will be sampled in subgroups, so that if special causes are present, the chance for differences between subgroups to appear will be maximized, while the chance for differences within a subgroup will be minimized. The strategy for one’s rational subgroup definition is very important and may depend upon one or more aspects of the process. How the rational subgroups are defined may affect the detection properties of the SPC chart. For example sampling several measurements at a specific discrete time points throughout the day will help the SPC chart to detect monotone shifts in the process. However, randomly sampling all process output across a sampling interval will result in a different rational group strategy, which may be better at detecting process shifts that go out-of-control and then back in between prespecified time points.
In addition to rational subgroups, it is important to pay attention to various patterns on the control chart. A control chart may indicate an out-of-control situation when one or more points lie outside of the control limits or when a nonrandom pattern of points appears. Such a pattern may or may not be monotone within a given run of points. The problem of pattern recognition associated with an out-of-control process requires both the use of statistical tools and knowledge about the process. A general statistical tool to analyze possible patterns of non-randomness is the runs test (Kenett and Zacks 2014, chapter 9).
As one might expect, having multiple rules for detecting out-of-control trends or patterns can lead to an increase in false alarms, particularly if a process is assumed to be out-of-control if at least one, out of many such rules, provides such indication. It may be possible to adjust the false positive rate for the simultaneous use of such rules, but this may be difficult as many such rules are not statistically independent. For example, one rule may be “one or more points outside of the control limits” while another rule may be “six points in a row with a monotone trend”. This is a situation where computer simulation can help to provide some insights regarding the probabilities of false alarms when using multiple rules for detecting out-of-control trends or patterns.
Typical control chart development is divided into two phases, Phase I and Phase II. The purpose of Phase I is to develop the center line and control limits for the chart, as well as to ascertain if the process is in control when operating in the sequential setting as intended. Phase I may also be a time when the process requires further tweaking to be brought into a state of control. The classical Shewhart control charts are generally very effective for Phase I because they are easy to develop and interpret, and are effective for detecting large changes or prolonged shifts in the process. In phase II, the process is now assumed to be reasonably stable so that phase II is primarily a phase of process monitoring. Here, we expect more subtle changes in the process over time, and so more refined SPC charts may be employed such as cumulative sum and Exponentially Weighted Moving Average (EMWA) control charts (Montgomery 2009, chapter 9).
The notion of “average run length” (ARL) is a good measure for evaluation a process in Phase II. The ARL associated with an SPC chart or an SPC method is the expected number of points that must be plotted before detecting an out-of-control situation. For the classical Shewhart control chart, the ARL = 1/p, where p is the probability that any point exceeds the control limits. This probability, p, can often be increased by taking a larger sample at each observation point. Another useful, and related measure, is the “average time to signal” (ATS). If samples are taken that are t hours apart, the ATS = ARLt. We can always reduce the ATS by increasing the process sampling frequency. In addition, the ARL and ATS can be improved by judicious use of more refined control chart methodology (in some cases through cumulative sum or EWMA control charts). For some control charts (e.g. Shewhart) the run time distribution is skewed so that the mean of the distribution may not be a good measure. As such, some analysts prefer to report percentiles of the run length distribution instead.
Many processes involve multiple quality measurements. As such, there are many situations where one needs to monitor multiple quality characteristics simultaneously. However, statistical process monitoring to detect out-of-control processes or trends away from target control requires special care, and possibly multiple SPC charts of different types. The naive use of a standard SPC chart for each of several measured quality characteristics can lead to false alarms as well as missing out-of-control process responses. False alarms can happen more often than expected with a single SPC chart because the probability of at least one false alarm out of several can be noticeably greater than the false alarm rate on an individual SPC chart. In addition, multivariate outliers can be missed with the use of only individual control charts. Because of this, special process monitoring methods have been developed for multivariate process monitoring and control.
One of the first methods to address multivariate process monitoring is the Hotelling T 2 control chart. This chart involves plotting a version of the Hotelling T 2 statistic against an upper control limit chi-square or F critical value. The Hotelling T 2 statistic can be modified to address either the individual or grouped data situation. However, an out-of-control signal by the Hotelling T 2 statistic does not provide any indication of what particular quality response or responses are responsible. In addition to SPC charts for individual quality responses, one can plot the statistics, 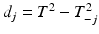 , where
, where 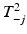 is the value of the T 2 statistic but with the jth quality response omitted.
is the value of the T 2 statistic but with the jth quality response omitted.
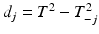 , where
, where 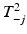 is the value of the T 2 statistic but with the jth quality response omitted.
is the value of the T 2 statistic but with the jth quality response omitted.Several other univariate control chart procedures have been generalized to the multivariate setting. As stated above, EWMA charts were developed to better detect small changes in the process mean (for a single quality response type). Analogously, multivariate EWMA chart methods have been developed to detect small shifts in a mean vector. In addition, some procedures have been developed to monitor the multivariate process variation by using statistics which are functions of the sample variance-covariance matrix. See Montgomery (2009, pp 516–517) for details.
When the number of quality responses starts to become large (more than 10 say), standard multivariate control chart methods start to become less efficient in that the ARL also increases. This is because any shifts in one or two response types become diluted in the large space of all of the quality responses. In such cases, it may be helpful to try to reduce the dimensionality if the problem by projecting the high-dimensional data into a lower dimensional subspace. One approach is to use principal components. For example, if the first two principal components account for a large proportion of the variation, one can plot the principal component scores labeled by their order within the process as given by the recorded data vectors. This is called a trajectory plot. Another approach is to collect the first few important principal components and then apply the multivariate EWMA chart approach to them (Scranton et al. 1996).
15.2.7 Acceptance Sampling
When lots of raw materials arrive at a manufacturing plant, it is typical to inspect such lots for defects or some measure related to raw material quality. In addition, pharmaceutical companies often inspect newly manufactured lots of product before making a decision about whether or not to release the product lot or patch for further processing or public consumption.
However, it is useful to note that the primary purpose of acceptance sampling is to sentence lots as acceptable or not; it is not to create a formal estimate of lot quality. In fact, most acceptance sampling procedures are not designed for estimation of lot quality Montgomery (2009). Acceptance sampling should not be a substitute for process monitoring and control. Nonetheless, the use of acceptance sampling plans over time produces a history of information which reflects on the quality of the process producing the lots or batches. In addition, this may provide motivation for process improvement work if too many lots or batches are rejected. See Chap. 20 for additional discussions on this and related ideas.
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


