Fig. 1
Schematic view of our computer-assisted planning and navigation of PAO. (a) The input surface models; (b) computer-assisted PAO planning; (c) the pre-operative planning output; (d) intra-operative PAO navigation for implementing the planned PAO surgery
Our system works in two stages: pre-operative planning stage and intra-operative navigation stage. The input to the pre-operative planning stage is 3D surface models of pelvis and femur generated from pre-operatively acquired CT data using a commercially available segmentation program (AMIRA, Visage Imaging, San Diego, USA). The pelvic local coordinate systems is then established using anatomical landmarks extracted from the CT data (see Fig. 1) which is defined on the anterior pelvic plane (APP) using the bilateral anterior superior iliac spines (ASISs) and the bilateral pubic tubercles [19]. After local coordinate system is established, a fully automatic detection of the acetabular rim is conducted using an improved algorithm [9] for the rim detection method of [16]. The detected acetabular rims allow for quantifying the acetabular morphology with parameters such as version, inclination, and acetabular coverage. After that, virtual reorientation procedure for acetabulum fragment is performed until an optimal biomechanics situation is obtained. The results from the planning stage are then passed to the intra-operative navigation stage [10] where a visual feedback is provided during the acetabular fragment reorientation procedure in order to achieve the planned situation.
2.1.2 Quantifying 3D Hip Joint Morphology
Accurate assessment of acetabular morphology and its relationship to the femoral head is essential for PAO planning. As soon as acetabular rim points are extracted, least-squares fitting is used to fit a plane to these points. The fitted plane then allows for computing acetabular inclination and anteversion [13] (see Fig. 1c). Additional hip morphological parameters such as the 3D LCE angle, the 3D femoral head extrusion index (EI), and the 3D acetabular coverage (AC) are computed as well (see Fig. 1c). LCE is depicted as an angle formed by a line parallel to the longitudinal pelvic axis and by the line connecting the center of the femoral head with the lateral edge of the acetabulum according to Wiberg [17]. EI is defined as the percentage of uncovered femoral head in comparison with the total horizontal head diameter according to Murphy et al. [11]. AC is defined to be a ratio between the area of the upper femoral head surface covered by the acetabulum and the area of the complete upper femoral head surface.
2.1.3 Virtual PAO Surgical Procedure
A virtual PAO procedure is conducted with our system as follows. First, a sphere is used to simulate osteotomy operation. The center of femoral head is taken as the center of the sphere whose radius and position can be interactively adjusted along lateral/medial, caudal/cranial, and dorsal/ventral directions, respectively, in order to approximate actual osteotomy operation (see Fig. 2a). After that, the virtual PAO procedure is conducted by interactively changing the inclination and the anteversion of the acetabulum fragment (see Fig. 2b). During the acetabulum fragment reorientation, 3D LCE angle, EI, and AC are computed in real time based on the reoriented acetabulum fragment and showed at the bottom of the screen (see Fig. 2b). Once a desired position is achieved, the realigned model is stored and transferred to the biomechanical analysis module for an FE simulation as explained in detail in the following section.


Fig. 2
Virtual PAO surgical procedure in our PAO planning system. (a) Virtual cutting operation is done with a sphere, whose radius and position can be interactively adjusted; (b) virtual reorientation operation is done by interactively adjusting anteversion and inclination angle of the acetabulum fragment
2.2 Patient-Specific Biomechanical Model
2.2.1 Mesh Generation
Bone surface models of the reoriented hip joints are imported into ScanIP software (Simpleware Ltd., Exeter, UK). While patient-specific cartilage models are essential in biomechanical simulation, it has been previously reported in [14] that the predicted optimal alignment of the acetabulum was not significantly sensitive to the choice of cartilage thickness distribution over the acetabulum. Therefore a 3D dilation operation was performed on femoral head and acetabular surfaces to create femoral and pelvic cartilage layers with a constant thickness as has been done in [1]. Reconstructed surfaces were smoothed with a recursive Gaussian filter to remove segmentation artifacts (Fig. 3a, c).
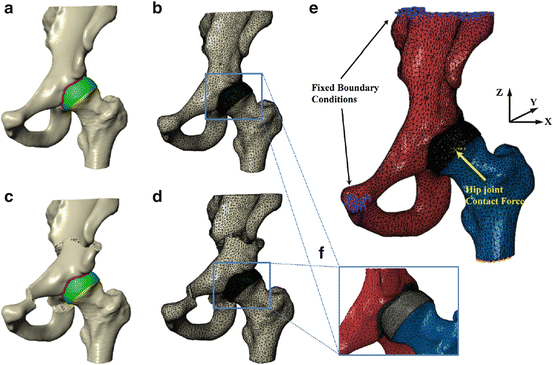

Fig. 3
Biomechanical simulation of contact pressure on acetabular cartilage. (a) Surface models for dysplastic hip; (b) volume meshes for dysplastic hip; (c) surface models for a planned situation after acetabulum fragment reorientation; (d) volume meshes for the planned situation; (e) boundary conditions and loading for biomechanical simulation; (f) coarse meshes for pelvic and femoral models, and refined meshes for pelvic and femoral cartilages
Surfaces were discretized using tetrahedral elements (Fig. 3b, d). Since the primary concern was focused on the joint contact, a finer mesh was employed for the cartilage than for the bone. Refined tetrahedral meshes were constructed for the cartilage layers using ScanFE module (Simpleware Ltd., Exeter, UK). Cortical bone surfaces were discretized using coarse tetrahedral elements. Trabecular bone was not included in the models, for it has little effect on predictions of contact stress as reported in [1]. Tied and sliding contact constraints were used in Abaqus/CAE 6.10 (Dassault Systmes Simulia Corp, Providence, RI) to define the cartilage-to-bone and cartilage-to-cartilage interfaces, respectively. It has been reported in [5] that the friction coefficient between articulating cartilage surfaces is very low, on the order of 0.01–0.02 in the presence of synovial fluid. Therefore, it is reasonable to neglect frictional shear stresses between contacting articular surfaces.
2.2.2 Material Property
Pelvic and femoral cartilages were modeled as homogeneous, isotropic, and linearly elastic material with Young’s Modulus E = 15 MPa and Poissons ratio = 0. 45. Cortical bone of pelvis and femur were modeled as homogeneous, isotropic material with elastic modulus E = 17 GPa and Poissons ratio = 0. 3 as has been used in [20].
2.2.3 Loading and Boundary Conditions
The loading and boundary conditions used in this paper resemble those used by Phillips et al. [15] (Fig. 3e). The top surface of pelvis and pubic areas were fixed, and the distal end of the femur was constrained to prevent displacement in the body x and y directions while being free in vertical z direction (Fig. 3e). The center of femoral head derived from a least-square sphere fitting was selected to be the reference node. The nodes of femoral head surface are constrained by the reference node via kinematic coupling. The fixed boundary condition model was then subjected to a loading condition as published in [4], representing a single leg stance situation with the resultant hip joint contact force acting at the reference node. Although CT scan was performed in the supine orientation and the loading condition of our biomechanical simulation is based on one-leg stance situation [4], previous work [14] has shown that there is no significant difference between the contact pressure in the Bergmanns reference frame and those in the supine reference frame. In addition, as pointed out by Armiger et al. [3], it is not an infrequent clinical practice to use the supine frame as an estimate of the standing frame. Therefore we believe our model makes good use of valuable, available data from Bergmanns work [4]. Following the loading specification in [15], the components of joint contact force along three axes are given as 195, 92, and 1,490 N, respectively, by assuming a constant body weight of 650 N for all subjects to remove any scaling effect of body weight on the absolute value of the contact pressure. The resultant force is applied based on anatomical co-ordinate system described in Bergmann et al. [4], whose local coordinate is defined with the x axis running between the centers of the femoral heads (positive running from the left femoral head to the right femoral head), the y axis pointing directly anteriorly, and the z axis pointing directly superiorly.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


