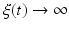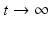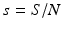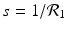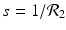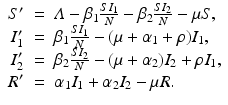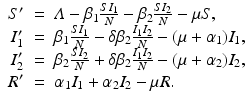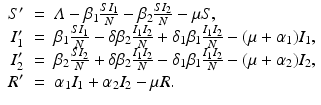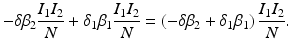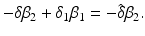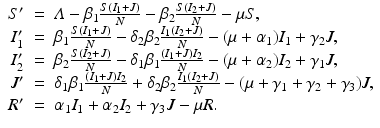(1)
Department of Mathematics, University of Florida, Gainesville, FL, USA
8.1 Competitive Exclusion Principle
The causative agents of diseases, such as viruses and bacteria, may be represented by multiple variants, called by the general name strains (or subtypes). The presence of multiple strains of a pathogen complicates our ability to combat the disease. For instance, in influenza, it is believed that each strain imparts permanent immunity, but drift evolution creates new strains, and in a new flu season, we can contract the disease again. There are other diseases whose causative agents are represented by multistrain pathogens. For example, Haemophilus influenzae, which is responsible for a range of infections, is represented by six serotypes: a, b, c, d, e, and f, as well as some variants that are not typeable. Streptococcus pneumonae is represented by 90 serotypes. Dengue virus has four serotypes. In this chapter, we study models with multiple strains.
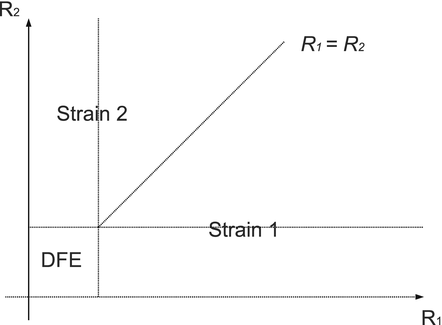
In ecology, the competitive exclusion principle is one of the main principles that govern species competition. The principle was first formulated as a law in the 1930s by the Russian ecologist Georgy Gause [64], who discovered it based on laboratory experiments. In short, the principle can be stated as complete competitors cannot coexist. In this section, we introduce through models the epidemiological context of this principle.
8.1.1 A Two-Strain Epidemic SIR Model
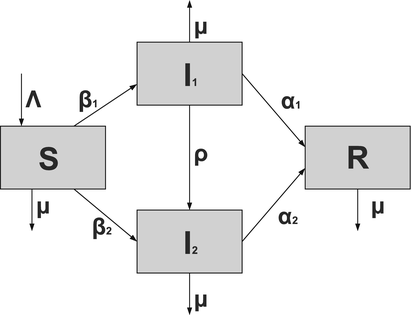
To account for the genetic variability of the pathogen, we investigate an SIR epidemic model with multiple strains. The the two-strain model has the following compartments: S(t) is the number of susceptible individuals at time t, I 1(t) is the number of individuals infected by strain one, I 2(t) is the number of individuals infected by strain two, and R(t) is the number of recovered individuals. We assume that each strain, once contracted, imparts permanent immunity to itself and to the other strain.
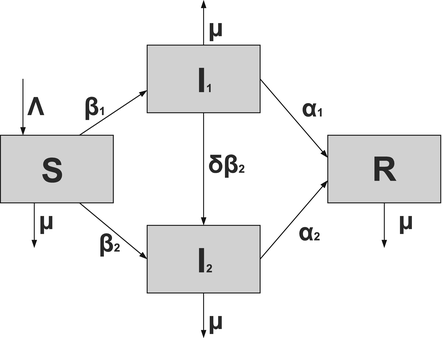
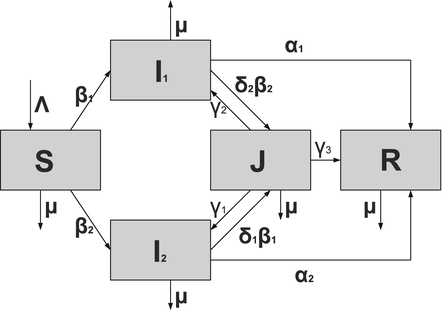
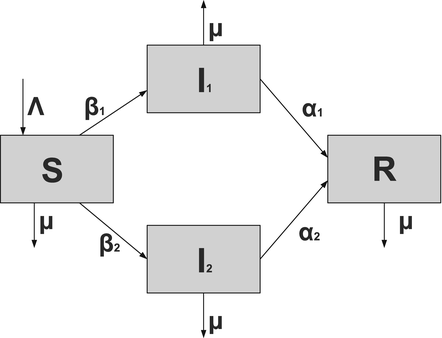
Susceptible individuals can become infected either by strain one at a transmission rate β 1 or by strain two at a transmission rate β 2. Those infected with strain one recover at a rate α 1, and those infected with strain two recover at a rate α 2. Susceptible individuals are recruited at a rate Λ. Individuals in all classes die at a natural death rate μ. The model is given below. The flowchart of the model is given in Fig. 8.1:
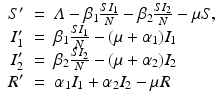
The total population size N is given by 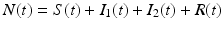 . Adding the equations above, we see that the equation of the total population size is the simplified logistic
. Adding the equations above, we see that the equation of the total population size is the simplified logistic 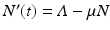 .
.
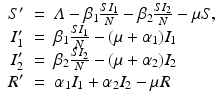
(8.1)
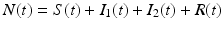 . Adding the equations above, we see that the equation of the total population size is the simplified logistic
. Adding the equations above, we see that the equation of the total population size is the simplified logistic 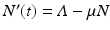 .
.
Fig. 8.1
A flowchart of an SIR model with two strains and perfect immunity
The next step will be to compute the equilibria. Working with a standard incidence allows us to consider the equilibrium equations of the proportions. For the equilibrial values of the variables S, I 1, I 2, and R, we set 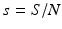 ,
, 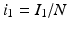 ,
, 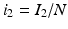 ,
, 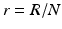 . Since N satisfies the equation
. Since N satisfies the equation 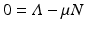 , and hence Λ = μ N, the equations for the equilibrium proportions are given by
, and hence Λ = μ N, the equations for the equilibrium proportions are given by
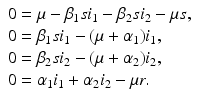
Model (8.1) has three equilibria. The model has a disease-free equilibrium in which neither strain one nor strain two is present. At the disease-free equilibrium, we have 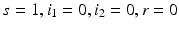 . Hence, the disease-free equilibrium in the original variables is given by
. Hence, the disease-free equilibrium in the original variables is given by 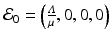 . In contrast to single-strain models, multistrain models have multiple reproduction numbers, one for each strain. To define the reproduction numbers associated with strain one and strain two, we have to look at the local stability of the disease-free equilibrium. Computing the Jacobian at the disease-free equilibrium yields
. In contrast to single-strain models, multistrain models have multiple reproduction numbers, one for each strain. To define the reproduction numbers associated with strain one and strain two, we have to look at the local stability of the disease-free equilibrium. Computing the Jacobian at the disease-free equilibrium yields
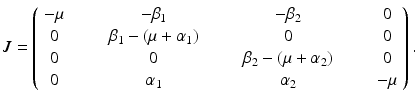
The characteristic equation 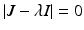 has one double eigenvalue
has one double eigenvalue 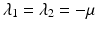 , and the following two eigenvalues:
, and the following two eigenvalues:
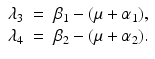
The disease-free equilibrium is locally asymptotically stable if λ 3 < 0 and λ 4 < 0. We notice that the eigenvalue λ 3 is associated with strain one and gives rise to the reproduction number of strain one, 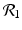 . The eigenvalue λ 4 is associated with strain two and gives rise to the reproduction number of strain two,
. The eigenvalue λ 4 is associated with strain two and gives rise to the reproduction number of strain two, 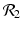 . Thus, we define
. Thus, we define

We have the following result:
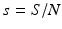 ,
, 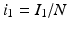 ,
, 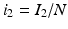 ,
, 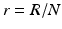 . Since N satisfies the equation
. Since N satisfies the equation 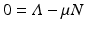 , and hence Λ = μ N, the equations for the equilibrium proportions are given by
, and hence Λ = μ N, the equations for the equilibrium proportions are given by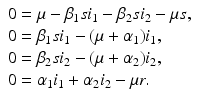
(8.2)
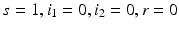 . Hence, the disease-free equilibrium in the original variables is given by
. Hence, the disease-free equilibrium in the original variables is given by 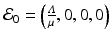 . In contrast to single-strain models, multistrain models have multiple reproduction numbers, one for each strain. To define the reproduction numbers associated with strain one and strain two, we have to look at the local stability of the disease-free equilibrium. Computing the Jacobian at the disease-free equilibrium yields
. In contrast to single-strain models, multistrain models have multiple reproduction numbers, one for each strain. To define the reproduction numbers associated with strain one and strain two, we have to look at the local stability of the disease-free equilibrium. Computing the Jacobian at the disease-free equilibrium yields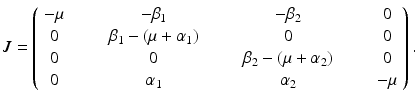
(8.3)
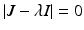 has one double eigenvalue
has one double eigenvalue 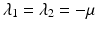 , and the following two eigenvalues:
, and the following two eigenvalues: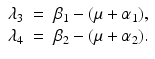
(8.4)
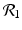 . The eigenvalue λ 4 is associated with strain two and gives rise to the reproduction number of strain two,
. The eigenvalue λ 4 is associated with strain two and gives rise to the reproduction number of strain two, 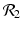 . Thus, we define
. Thus, we define
(8.5)
Proposition 8.1.
The disease-free equilibrium of system (8.1) is locally asymptotically stable if both reproduction numbers are less than 1, that is if
 The disease-free equilibrium is unstable if at least one of the above inequalities is reversed.
The disease-free equilibrium is unstable if at least one of the above inequalities is reversed.

8.1.2 The Strain-One- and Strain-Two-Dominance Equilibria and Their Stability
A strain-one-dominance equilibrium is a boundary equilibrium in which strain one is present i 1 ≠ 0, while strain two is not present i 2 = 0. From the second equation in (8.2), we have
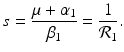 We need s < 1 for it to be a proper fraction. Thus, for a strain-one-dominance equilibrium to be meaningful, we need
We need s < 1 for it to be a proper fraction. Thus, for a strain-one-dominance equilibrium to be meaningful, we need 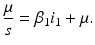
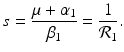
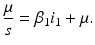
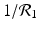 and solving for i 1, we have
and solving for i 1, we have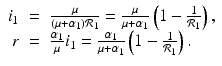
(8.6)
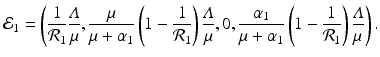
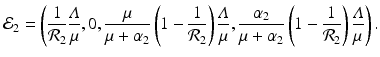

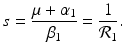
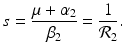
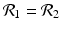
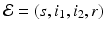
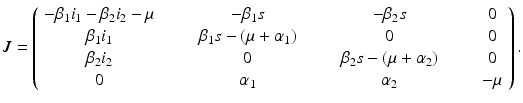
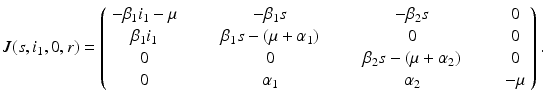
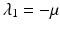
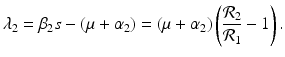
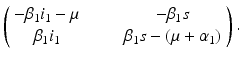
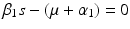
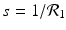
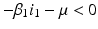
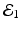
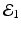
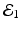
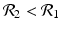
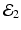
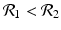
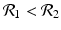
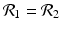
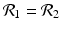
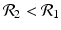
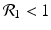
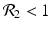
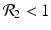
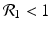
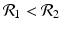
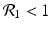
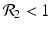
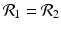
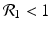
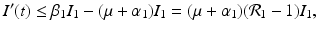
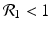
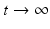
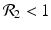
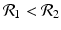
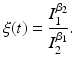
![$$\displaystyle{\xi ' = \frac{\beta _{2}I_{1}^{\beta _{2}-1}I_{1}'I_{2}^{\beta _{1}} -\beta _{1}I_{1}^{\beta _{2}}I_{2}'I_{2}^{\beta _{1}-1}} {[I_{2}^{\beta _{1}}]^{2}}.}$$](/wp-content/uploads/2016/11/A304573_1_En_8_Chapter_Equk.gif)
![$$\displaystyle\begin{array}{rcl} & & \beta _{2}I_{1}^{\beta _{2}-1}I_{ 2}^{\beta _{1} }[\beta _{1}I_{1}s - (\mu +\alpha _{1})I_{1}] -\beta _{1}I_{1}^{\beta _{2} }I_{2}^{\beta _{1}-1}[\beta _{ 2}I_{2}s - (\mu +\alpha _{2})I_{2}] \\ \quad & =& \beta _{2}I_{1}^{\beta _{2} }I_{2}^{\beta _{1} }[\beta _{1}s - (\mu +\alpha _{1})] -\beta _{1}I_{1}^{\beta _{2} }I_{2}^{\beta _{1} }[\beta _{2}s - (\mu +\alpha _{2})] \\ \quad & =& I_{1}^{\beta _{2} }I_{2}^{\beta _{1} }[\beta _{1}\beta _{2}s -\beta _{2}(\mu +\alpha _{1}) -\beta _{1}\beta _{2}s +\beta _{1}(\mu +\alpha _{2})] \\ \quad & =& I_{1}^{\beta _{2} }I_{2}^{\beta _{1} }(\mu +\alpha _{1})(\mu +\alpha _{2})[\mathcal{R}_{1} -\mathcal{R}_{2}]. {}\end{array}$$](/wp-content/uploads/2016/11/A304573_1_En_8_Chapter_Equ11.gif)
![$$\displaystyle{\xi '(t) = \frac{I_{1}^{\beta _{2}}I_{2}^{\beta _{1}}(\mu +\alpha _{1})(\mu +\alpha _{2})[\mathcal{R}_{1} -\mathcal{R}_{2}]} {[I_{2}^{\beta _{1}}]^{2}}.}$$](/wp-content/uploads/2016/11/A304573_1_En_8_Chapter_Equl.gif)
![$$\nu = (\mu +\alpha _{1})(\mu +\alpha _{2})[\mathcal{R}_{1} -\mathcal{R}_{2}]$$](/wp-content/uploads/2016/11/A304573_1_En_8_Chapter_IEq61.gif)