Chapter 5
Multi-centre trials and meta-analyses
In this chapter, we consider the analysis of data that are collected from several centres or trials. Such datasets in which observations have a natural grouping can be described as hierarchical. Use of a random effects model to analyse a hierarchical dataset often leads to results that can be generalised more widely. Section 5.1 provides an introduction to multi-centre trials; the implications of fitting different models are considered in Section 5.2; a worked example is given in Section 5.3; some general points specific to hierarchical datasets are made in Section 5.4; and sample size estimation methods are introduced in Section 5.5. Meta-analysis is considered in Section 5.6 and an example follows in Section 5.7.
5.1 Introduction to multi-centre trials
5.1.1 What is a multi-centre trial?
A multi-centre trial is carried out at several centres because insufficient patients are available for the study at any one centre, or with the deliberate intention of assessing the effectiveness of treatments in several settings. Sometimes, there will be extra variability in treatment effect estimates, which can be due to differences between the centres (e.g. different investigators, types of patients, climates). This extra variation can be taken into account in the analysis by including centre and centre·treatment effects as random effects in the model. Such variation is likely to be most noticeable in trials that do not compare drugs. For example, in a trial to compare surgical procedures, there may be varying levels of experience available at each centre with the different procedures. This will lead us to expect a positive variance component for the centre·treatment effects.
5.1.2 Why use mixed models to analyse multi-centre data?
When centre and centre·treatment effects are fitted as random, allowance is made for variability in the magnitude of the treatment effects between centres. However, deciding whether centre and centre·treatment effects should be fixed or random is often the subject of debate. In practice, the choice will depend on whether treatment estimates are to relate only to the set of centres used in the study or, more widely, to the circumstances and locations of which the trial centres can be regarded as a sample. In the former case, local treatment estimates for the sampled set of individual centres are obtained by fitting centre and centre·treatment effects as fixed. To obtain global treatment estimates, centre and centre·treatment effects should be fitted as random. When this is done, the standard error of treatment differences is increased to reflect the heterogeneity of the treatment effects across centres.
If the centre·treatment term is omitted, there is a choice of whether to fit centre effects as fixed or random. Taking centre effects as random can increase the accuracy of treatment estimates, since information from the centre error stratum is used in addition to that from the residual stratum. Thus, it is nearly always beneficial to fit centres as random, regardless of whether a local or global interpretation is required. The amount of extra information will depend on the degree of treatment imbalance within the centres and the relative sizes of the variance components.
In the analysis of multi-centre trials, it is important to check whether results from any particular centre are outlying. If this occurs, it may be an indication that a centre has not followed the protocol correctly. In the fixed effects model, spurious outlying estimates caused by random variation may occur, particularly in small centres. In contrast, the shrunken estimates of centre and centre·treatment effects obtained by the random effects model do not have this problem.
5.2 The implications of using different analysis models
In this section, we look more closely at the implications of fitting centre and centre·treatment effects as fixed or random. We will consider four different models, and in each of them treatment effects and baseline effects (if available) are fitted as fixed.
5.2.1 Centre and centre·treatment effects fixed
Treatments effects
These are estimated with equal weight given to results from each centre regardless of size. If centre sizes vary greatly, this can cause results to differ markedly from analyses not fitting centre·treatment effects as fixed. Another potential difficulty with this method is that treatment effects cannot be estimated at all unless all treatments are received at every centre. For example, if no patients received treatment A at one centre, then all comparisons involving treatment A would be non-estimable. In practice, we note, however, that this problem could be resolved by the amalgamation of centres with a small number of patients.
Treatment standard errors
These are based on the residual (within-centre) variation. The variance (SE)2 of a treatment difference is given by
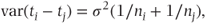
where σ2 is the residual variance and ni and nj are the number of patients receiving treatments i and j. When an equal number of patients, r, receive each treatment at each of c centres, we have ni = rc and the variance can be written as follows:
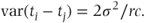
This variance will always be less than or equal to that for the model fitting centre·treatment effects as random (see Section 5.2.3).
Outlying centres
These can be determined from the centre and centre·treatment effect means. However, the estimates can be misleading for small centres, which could appear outlying owing only to random variation.
Inference
This strictly applies only to those centres that were included in the trial.
5.2.2 Centre effects fixed, centre·treatment effects omitted
This fixed effects model is often used when the centre·treatment effects in the previous model are non-significant. However, in practice, there is often a lack of power to detect small centre·treatment effects, and hence variability in the treatment effects across centres is often ignored.
Treatment estimates
These take account of differing centre sizes and are not estimated with equal weight given to results from each centre as in the previous model.
Treatment standard errors
These are based on the residual (within-centre) variation. The variances of treatment differences are given by the formula used in the previous model.
Outlying centres
These can be determined from the centre means. However, again, these can be misleading for small centres that could be apparently outlying owing only to random variation.
Inference
This strictly applies only to those centres that were included in the trial. However, extrapolation of the inferences regarding the effect of treatment to other centres seems more reasonable when an assumption has been made that the treatment effect does not depend on the centre in which it has been applied.
5.2.3 Centre and centre·treatment effects random
Unlike the commonly used fixed effects approach of dropping a non-significant centre·treatment interaction, centre·treatment effects are retained in the random effects model, provided the centre·treatment variance component,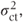 
is positive. Thus, variation in treatment effects across centres is allowed even though its existence may not have been ‘proven’ by a significance test.
Treatment estimates
These take account of differing centre sizes. They are estimated using information from the centre·treatment error stratum and also from the centre stratum if treatment effects are not balanced across centres. They are estimable even if some treatments are not received at every centre.
Treatment standard errors
Treatment standard errors are based on the centre·treatment variation. If an equal number of patients receive each treatment at every centre, the variance of treatment effect differences can be obtained as
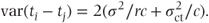
Thus, the variance is directly related to the size of the centre·treatment variance component,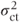 
, and the number of centres sampled, c. It is always expected to be greater than the fixed effects model variance, 2σ2/rc, provided 
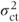is not allowed to be negative.
The variance is not as easily specified when centre sizes are unequal. However, if the proportion of patients allocated to each treatment is the same across centres, the variance is of the form
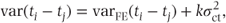
where varFE(ti − tj) is the fixed effects model variance and k is a positive constant. Thus, the variance is again always expected to be greater than or equal to that in the fixed effects model.
In most situations, though, the proportions of patients receiving each treatment will differ to some extent from centre to centre. When this is the case, a general formula for the variance cannot be specified. The effect of the centre·treatment variance component will, however, still cause an increase in the variance of the treatment differences.
Outlying centres
These can be determined using the shrunken centre and centre·treatment estimates. Shrinkage is greater for small centres, and therefore spurious outlying estimates will not be obtained for small centres.
Inference
This relates to the ‘population’ of possible centres from which those in the trial can be regarded as a random sample.
5.2.4 Centre effects random, centre·treatment effects omitted
This model is useful when local estimates are required, since smaller treatment standard errors are often obtained compared with a fixed effects model by recovering extra information from the centre error stratum.
Treatment estimates
These take account of differing centre sizes. Additional information on treatments is recovered from the centre error stratum.
Treatment standard errors
These are based on the residual (within-centre) variation. When the proportion of patients allocated to each treatment is the same across centres, the variances of treatment differences are given by the formula used in the first fixed effects model. When it is not, the variance is expected to be less, since extra information is recovered on treatment effects from the centre error stratum.
Outlying centres
These can be determined using the shrunken centre estimates. Shrinkage is greater for small centres, and therefore spurious outlying estimates are not obtained for small centres.
Inference
This relates to the only sampled centres. Only under the strong assumption that there is no centre·treatment interaction, inferences can be applied to the population of centres from which those in the trial can be considered as a sample.
5.3 Example: a multi-centre trial
We have already considered in some detail the analysis of a multi-centre trial of treatments for hypertension in Sections 1.3 and 2.5. Here, we discuss the interpretation of the results from these analyses in detail and consider estimates of treatment effects by centre.
Results from fixed and random effects’ analyses of DBP are summarised in Table 5.1. An initial fixed effects model including centre·treatment effects was also fitted. However, overall treatment effects were not estimable in this model, because all treatments were not received at every centre (see Table 1.1 in Section 1.3). This model gave a non-significant p – value for centre·treatment effects (p = 0.19), and thus the usual ‘fixed effects’ approach would have been to remove centre·treatment effects to give Model 1.
Table 5.1 Results from fixed and random effects analyses of diastolic blood pressure.
| Model | Fixed effects | Random effects | Method | |
| 1 | Baseline, treatment, centre | OLS | ||
| 2 | Baseline, treatment | Centre | REML | |
| 3 | Baseline, treatment | Centre, treatment·centre | REML | |
| Treatment effects (SEs) | ||||
| Model | Baseline | A − B | A − C | B − C |
| 1 | 0.22 (0.11) | 1.20 (1.24) | 2.99 (1.23) | 1.79 (1.27) |
| 2 | 0.22 (0.11) | 1.03 (1.22) | 2.98 (1.21) | 1.95 (1.24) |
| 3 | 0.28 (0.11) | 1.29 (1.43) | 2.93 (1.41) | 1.64 (1.45) |
| Variance components | ||||
| Model | Centre | Treatment·centre | Residual | |
| 1 | – | – | 71.9 | |
| 2 | 7.82 | – | 70.9 | |
| 3 | 6.46 | 4.10 | 68.4 | |
The centre·treatment variance component is positive in Model 3, and this leads to an increase in the treatment standard errors over the fixed effects models (as indicated by the variance formulae given in Section 5.2). However, note that the baseline standard error is similar between the models. This is because baseline effects are estimated at the residual error level and not at the centre·treatment level. Results from Model 3 can be related to the potential population of centres. Since there are 29 centres, there are no problems arising from an inadequate number of DF for the variance components, and we can be confident in presenting these results if global inference is required.
The centre variance component is positive in Models 2 and 3, and therefore some information on treatments will be recovered from the centre error stratum. However, the standard errors in Model 2 are only slightly smaller than in Model 1, indicating that only a small amount of information has been recovered. Also, some of the improvement in the standard error may be due to the smaller residual variance that has resulted from the use of this model.
Plots of the centre and centre·treatment effects from Model 3 were used in Section 2.5 to assess the normality of the random effects and to check whether any centres were outlying. In addition, we can now take differences between the centre·treatment effects to calculate treatment effect estimates for each centre. In Model 3, these will be shrunken towards the overall treatment mean. We illustrate this by calculating the treatment difference A–C for just the first eight centres in the study. Unshrunken fixed effects estimates are also calculated for comparison using results from the initial model (fitting treatment, centre and centre·treatment effects as fixed).
| Treatment estimates (SE) | |||
| Centre | Number of patients | Fixed model | Random model |
| 1 | 39 | 3.81 (3.34) | 3.19 (2.94) |
| 2 | 10 | −5.67 (6.80) | 1.56 (3.40) |
| 3 | 8 | 25.66 (7.63) | 6.05 (3.40) |
| 4 | 12 | −0.12 (5.90) | 2.42 (3.39) |
| 5 | 11 | 14.12 (7.21) | 4.56 (3.40) |
| 6 | 5 | 2.89 (8.37) | 3.03 (3.39) |
| 7 | 18 | 7.38 (4.82) | 4.22 (3.31) |
| 8 | 6 | −4.68 (8.33) | 2.15 (3.39) |
It can be seen that, in general, shrinkage is towards the overall treatment difference of 2.92 (although this is not the case for all centres, because the models make different adjustments for baseline effects). The relative shrinkage (i.e. (fixed estimate–random estimate)/(fixed estimate)) is usually greatest for the smaller centres. The standard errors of the random effects estimates are smaller than those of the fixed effects estimates because the random effects model utilises information on the treatment effects in the full sample as well as information from the centre of interest. By contrast, the fixed effects standard errors do not utilise the full sample information and are larger because they are calculated using only information from the centre of interest. This also causes the fixed effects standard errors to vary greatly between the centres because they are directly related to the centre sizes. It is difficult to determine whether any of the centres are outlying using the fixed effects estimates because they need to be considered bearing in mind centre size. For example, at centre 3 a very large treatment difference is given by the fixed estimate, but the shrunken random estimate appears acceptable. We note that the standard errors of the random effects estimates have increased by around 20% from those reported in the first edition of this book, by use of the Kenward–Roger option.
SAS code and output
Variables
centre= centre number,
treat= treatment (A, B, C),
patient= patient number,
dbp= diastolic blood pressure at last attended visit,
dbp1= baseline diastolic blood pressure.
The SAS code to produce the main results is given at the end of Section 2.5. Here, we give the code for obtaining the shrunken and unshrunken treatment effects at the first eight centres. PROC MIXED is used first to fit Model 3. ESTIMATE statements are included to calculate the shrunken treatment differences at the first eight centres. Next, a fixed effects model is fitted, which again uses ESTIMATE statements to calculate (unshrunken) treatment differences. Two datasets, ‘random’ and ‘fixed’, are then created to extract and label the random and fixed effects estimates. The rest of the code listed is concerned with merging and printing the two sets of estimates.
PROC MIXED; CLASS centre treat;
TITLE ‘RANDOM EFFECTS MODEL’;
MODEL dbp = dbp1 treat/DDFM = KENWARDROGER;
RANDOM centre centre*treat;
ESTIMATE ‘A-C,1’ treat 1 0 -1; centre*treat 1 0 -1;
ESTIMATE ‘A-C,2’ treat 1 0 -1| centre*treat 0 0 0 1 0 -1;
ESTIMATE ‘A-C,3’ treat 1 0 -1| centre*treat
0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,4’ treat 1 0 -1| centre*treat
0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,5’ treat 1 0 -1| centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,6’ treat 1 0 -1| centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,7’ treat 1 0 -1| centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0-1;
ESTIMATE ‘A-C,8’ treat 1 0 -1| centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ODS OUTPUT ESTIMATES = random;
PROC MIXED; CLASS centre treat;
TITLE ‘FIXED EFFECTS MODEL’;
MODEL dbp = dbp1 treat centre centre*treat;
ESTIMATE ‘A-C,1’ treat 1 0 -1 centre*treat 1 0 -1;
ESTIMATE ‘A-C,2’ treat 1 0 -1 centre*treat 0 0 0 1 0 -1;
ESTIMATE ‘A-C,3’ treat 1 0 -1 centre*treat 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,4’ treat 1 0 -1 centre*treat
0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,5’ treat 1 0 -1 centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,6’ treat 1 0 -1 centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,7’ treat 1 0 -1 centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ESTIMATE ‘A-C,8’ treat 1 0 -1 centre*treat
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 -1;
ODS OUTPUT ESTIMATES = fixed;
DATA random; SET random;
centre=substr(label,5,2)*1;
est=estimate;
se=stderr;
KEEP centre est se;
DATA fixed; SET fixed;
centre=substr(label,5,2)*1;
estf=estimate;
sef=stderr;
KEEP centre estf sef;
* Summarise original dataset ‘a’ to obtain centre means;
PROC SORT DATA=a; BY centre;
PROC MEANS NOPRINT DATA=a; BY centre; VAR dbp; OUTPUT
OUT=freq N=freq;
DATA b; MERGE fixed random freq; BY centre;
IF centre<=8;
shrink=abs(estf-est);
PROC PRINT SPLIT=‘*’ noobs; VAR centre freq estf sef est se;
LABEL centre=‘**CENTRE’
freq=‘PATIENTS*AT*CENTRE’
estf=‘FIXED*MODEL*ESTIMATE’
sef=‘FIXED*MODEL*SE’
est=‘RANDOM*MODEL*ESTIMATE’
se=‘RANDOM*MODEL*SE’
shrink=‘SHRINKAGE’;
FORMAT estf est se sef 8.2;RANDOM EFFECTS MODEL | |
The Mixed Procedure | |
Model Information | |
Data Set | WORK.A |
Dependent Variable | dbp |
Covariance Structure | Variance Components |
Estimation Method | REML |
Residual Variance Method | Profile |
Fixed Effects SE Method | Prasad-Rao-Jeske- |
Kackar-Harville | |
Degrees of Freedom Method | Kenward-Roger |
Dimensions | |
Covariance Parameters | 3 |
Columns in X | 5 |
Columns in Z | 108 |
Subjects | 1 |
Max Obs Per Subject | 288 |
Number of Observations | |
Number of Observations Read | 288 |
Number of Observations Used | 288 |
Number of Observations Not Used | 0 |
Iteration History | |||
Iteration | Evaluations | -2 Res Log Like | Criterion |
0 | 1 | 2072.30225900 | |
1 | 3 | 2055.64188178 | 0.00000322 |
2 | 1 | 2055.63936685 | 0.00000000 |
Convergence criteria met. | |
Covariance Parameter | |
Estimates | |
Cov Parm | Estimate |
centre | 6.4628 |
centre*treat | 4.0962 |
Residual | 68.3677 |
Fit Statistics | |
-2 Res Log Likelihood | 2055.6 |
AIC (smaller is better) | 2061.6 |
AICC (smaller is better) | 2061.7 |
BIC (smaller is better) | 2065.7 |
Type 3 Tests of Fixed Effects | ||||
Num | Den | |||
Effect | DF | DF | F Value | Pr > F |
dbp1 | 1 | 284 | 6.16 | 0.0137 |
treat | 2 | 25 | 2.16 | 0.1364 |
Estimates | |||||
Standard | |||||
Label | Estimate | Error | DF | t Value | Pr > |t| |
A-C,1 | 3.1914 | 2.9446 | 6.68 | 1.08 | 0.3160 |
A-C,2 | 1.5596 | 3.4033 | 2.48 | 0.46 | 0.6838 |
A-C,3 | 6.0493 | 3.3976 | 2.31 | 1.78 | 0.1999 |
A-C,4 | 2.4208 | 3.3894 | 2.82 | 0.71 | 0.5297 |
A-C,5 | 4.5609 | 3.3985 | 2.43 | 1.34 | 0.2910 |
A-C,6 | 3.0296 | 3.3878 | 2.17 | 0.89 | 0.4591 |
A-C,7 | 4.2176 | 3.3132 | 3.55 | 1.27 | 0.2799 |
A-C,8 | 2.1511 | 3.3887 | 2.17 | 0.63 | 0.5859 |
FIXED EFFECTS MODEL | |
The Mixed Procedure | |
Model Information | |
Data Set | WORK.B |
Dependent Variable | dbp |
Covariance Structure | Diagonal |
Estimation Method | REML |
Residual Variance Method | Profile |
Fixed Effects SE Method | Model-Based |
Degrees of Freedom Method | Residual |
Class Level Information | ||
Class | Levels | Values |
centre | 29 | 1 2 3 4 5 6 7 8 9 11 12 13 14 |
15 18 23 24 25 26 27 29 30 31 | ||
32 35 36 37 40 41 | ||
treat | 3 | A B C |
Dimensions | |
Covariance Parameters | 1 |
Columns in X | 113 |
Columns in Z | 0 |
Subjects | 1 |
Max Obs Per Subject | 288 |
Number of Observations | |
Number of Observations Read | 288 |
Number of Observations Used | 288 |
Number of Observations Not Used | 0 |
Covariance Parameter | |
Estimates | |
Cov Parm | Estimate |
Residual | 69.2614 |
Fit Statistics | |
-2 Res Log Likelihood | 1558.1 |
AIC (smaller is better) | 1560.1 |
AICC (smaller is better) | 1560.1 |
BIC (smaller is better) | 1563.5 |
Type 3 Tests of Fixed Effects | ||||
Num | Den | |||
Effect | DF | DF | F Value | Pr > F |
dbp1 | 1 | 208 | 0.99 | 0.3198 |
treat | 2 | 208 | 1.24 | 0.2905 |
centre | 28 | 208 | 1.98 | 0.0038 |
centre*treat | 48 | 208 | 1.20 | 0.1884 |
Estimates | |||||
Standard | |||||
Label | Estimate | Error | DF | t Value | Pr > |t| |
A-C,1 | 3.8081 | 3.3364 | 208 | 1.14 | 0.2550 |
A-C,2 | -5.6720 | 6.8036 | 208 | -0.83 | 0.4054 |
A-C,3 | 25.6559 | 7.6275 | 208 | 3.36 | 0.0009 |
A-C,4 | -0.1189 | 5.8972 | 208 | -0.02 | 0.9839 |
A-C,5 | 14.1230 | 7.2085 | 208 | 1.96 | 0.0514 |
A-C,6 | 2.8891 | 8.3700 | 208 | 0.35 | 0.7303 |
A-C,7 | 7.3811 | 4.8201 | 208 | 1.53 | 0.1272 |
A-C,8 | -4.6825 | 8.3284 | 208 | -0.56 | 0.5746 |
The table of shrunken and unshrunken treatment estimates is given within the main text.
5.4 Practical application and interpretation
In this section we consider some general points relating specifically to analyses of multi-centre data.
5.4.1 Plausibility of a centre·treatment interaction
One approach to analysing multi-centre trials of drug treatments works from the premise that it is not plausible for a treatment effect to vary across centres. If it does, it is deemed a fault with the study design. If a significant centre·treatment interaction is not detected, then the design is assumed to be sound and global inference is made from a model not allowing for any variation in treatment effects between centres. However, a drug effect can sometimes vary owing to differences in the centre populations even when they are defined within the constraints of the protocol. For example, one drug may work better on severely ill patients than another but less well on moderately ill patients. Thus, a centre containing more severely ill patients could produce larger treatment effects than centres containing a more even mixture of patients. For this reason, it is our belief that centre·treatment effects are always plausible, and that if global inference is required from a multi-centre trial, then the random effects model is likely to be the most appropriate.
Interactions are often even more plausible in trials not involving drugs. For example, in a trial of surgical techniques, one centre may have much more expertise with one technique than another. In this type of trial, a random effects model should almost always be used in order to provide global inference.
5.4.2 Generalisation
Consideration of different interpretations of results from fixed effects and random effects analyses brings the issue of generalisation to the fore. Results are often generalised from the situation in which they were sampled to other situations. However, strictly speaking, results should only be generalised when the study sample has been taken at random from the whole population of interest. Since centres are rarely sampled at random, even the global results from a multi-centre trial cannot be formally generalised to the population of possible centres.
There are analogies, though, with a single-centre study. In such studies, patients are not usually selected at random from the potential population of patients available at the centre. However, results are usually seen as some indication of those expected in the future both in the same centre and elsewhere.
Thus, in practice, generalisation needs to be by degree and will always to some extent involve subjective judgements, for example of how well the centres (or patients) sampled represent their full potential populations. Multi-centre studies would usually be considered more generalisable than single-centre studies even though the centres are not randomly sampled, and even if a fixed effects model is employed.
5.4.3 Number of centres
The accuracy with which variance components are estimated is dependent on the number of centres used. If the centre·treatment variance component is inaccurate, then this will have a direct effect on the accuracy of the treatment standard errors (calculated as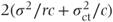 
when data are balanced). Thus, if a study uses only a few centres (say less than about five), 
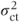and hence the treatment effect standard error may not be accurate. In this situation a random effects analysis may be inadvisable, although it could used to provide a rough idea of the global treatment estimates. However, the main conclusions from the study should be based on local results obtained from a fixed effects model, usually omitting the centre·treatment interaction term.
5.4.4 Centre size
Sometimes, a trial contains several centres that stop participating in the trial after recruiting only a few patients. Since little information is available for measuring effects at such centres, a strategy that is often adopted is to combine such centres into one centre in the analysis. This has most use when a fixed effects model is used, because the centre·treatment interaction can then be assessed more effectively. However, in a mixed model, it usually makes little difference whether such centres are combined together or fitted separately.
5.4.5 Negative variance components
If centre·treatment effects are retained but the centre variance component estimate is negative, then centre effects could be either removed altogether from the model or retained with their variance component constrained to zero. Although the same effect estimates will be obtained using either approach, the DF used by the significance tests will differ. The latter option of retaining the centre effect DF is perhaps the most satisfactory because centre·treatment effects are retained. If both centre and centre·treatment variance components are negative, then they can be removed from the model and the data analysed as a simple between-patient trial. Inference can still be made globally to the population of centres, since there is no variation in the treatment effect across centres.
5.4.6 Balance
In models including treatment·centre effects balance will only be achieved in the unlikely situation where there are an equal number of patients per treatment per centre (this condition is also required to achieve balance across random effects). Treatment mean estimates from either a fixed or random effects model will then equal the raw treatment means. In the more usual situations where there are unequal numbers of patients per treatment per centre, treatment means will differ between fixed effects and random effects models.
In models omitting centre·treatment effects, balance across random effects is achieved when treatments are allocated in equal proportions at each centre (even if the overall centre sizes vary). Treatment estimates are then the same, regardless of whether centre effects are taken as fixed or random. However, if treatments are not allocated in equal proportions at each centre, treatment estimates will differ between the models because information is combined from both the centre and residual error strata in the random effects model.
5.5 Sample size estimation
When designing a multi-centre trial with the intention of estimating global treatment effects, sample size estimates can be calculated in a way that takes into account variation of treatment effects between centres. Here, we will obtain sample sizes that can be used for trials, based on considering differences between pairs of treatments.
5.5.1 Normal data
In Section 5.2, the variance of the difference between a pair of treatments in a balanced dataset was given as
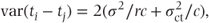
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
