Fig. 4.1
Diagram of hydrodynamic lubrication in joints
However, it became shortly apparent that this hypothesis was unable to explain the extremely small friction coefficients that are observed in real joints. It is because that, on the one hand, the relative sliding velocity of bone surfaces would never exceed several centimeters per second. The calculation of the least thickness of the lubricating film following the theory of Reynolds ignores the viscoelastic properties of rubbing surfaces, on the other hand, and yields an extremely small friction value, i.e. of the order of magnitude of the cartilage roughness [8]. Irrespective these shortcomings, this hypothesis enjoyed enormous import because it was a first effort of application of achievements of other sciences relating to the functioning of joints and pushed consecutive studies in this direction.
McConnell’s study truly provoked sizeable interest to the problem of lubrication in joints. T.E. Stanton proposed at that time a gravitation pendulum for experimental assessment of friction in joints [7], because the curve of attenuation enabled to judge both about the friction value and about the pattern of friction in the specimens of biological and non-biological materials that served as load-carrying components. The linear curve of attenuation of oscillations of the pendulum, i.e. independent of the sliding friction of the load-carrying unit, was considered typical for boundary lubrication, while the exponential attenuation curve, i.e. dependent on the sliding velocity, was considered typical for hydrodynamic or film lubrication of [7, 9].
E.S. Jones was the first in 1934 to measure experimentally the friction coefficient in animal joints [7, 10]. He established that the friction coefficient of knee joints in the lubricating synovial fluid or saline solution was within 0.02, meanwhile the dry friction coefficient increased by an order of magnitude. It was also noted the rubbing cartilage surfaces in the latter case would quickly disintegrate. Later studies confirmed the obtained data convincingly by showing that the friction coefficient in animal joints ranged from 0.005 to 0.02 [9, 10].
Jones some time later, in 1936, continued his studies by experimenting with the pendulum workbench in which an interphalangeal joint served as a load-carrying unit [7, 11]. These experiments revealed that the amplitude of pendulum oscillations was gradually diminishing exponentially; so he concluded that viscous dumping existed in the joint, hence, a fluid film lubricates the latter. However, disregarding these results, Jones recognized the fact of hydrodynamic lubrication of the joints just partly. The circumstance guided him that joints are not always in motion, on the one hand, so no high velocities develop in it, on the other hand. Even at the moment after the onset of very slow movements, the rubbing cartilaginous surfaces produce a rather low friction coefficient. Whence Jones concluded that there is mixed lubrication in the joints, i.e. hydrodynamic or film lubrication in the process of motion and boundary now when motion begins or ends. Nevertheless, he failed to demonstrate that the synovial fluid possessed the necessary lubricity to satisfy common [5, 7].
Almost 20 years later no new theories of lubrication of joints ever appeared. At that time, the synovial fluid and the hyaluronic acid discovered in it, as well as the characteristics of their physico-chemical properties arrested attention of the researchers entirely [5]. Only in the beginning of the 50 s, the researchers resumed studies of the mechanism of lubrication of joints. McConnell was the first to advance a possibility of the hydrodynamic theory to the joints. He began to doubt if the assumption was right that there is a single mechanism that produces an effective system of their lubrication [7]. Nevertheless, he continued to believe that the additional structures, like the meniscus and the fatty body, produce converging wedges of lubrication at slow sliding speeds when joints reciprocate. E. Gardner developed his point of view about how essential were the hydrodynamic principles of lubrication of joints. Like Jones, he admitted that boundary lubrication could exist in certain situations.
In that epoch, it became evident that the hydrodynamic theory of lubrication of Reynolds assuming stiff contacting surfaces has limitations when explaining the features of lubrication of articular surfaces easily deformable in the dynamic contact. Grubin removed these limitations in 1949 when he included elastic deformation of coupled surfaces into his calculations and demonstrated theoretically that the lubricating had a larger thickness than it had assumed before. Hence, the hydrodynamic lubrication is possible in the conditions that had presumably permitted only the boundary lubrication [5]. In 1959, D. Dowson and G.R. Higginson found a justification for the theory of Grubin and applied the term elastohydrodynamic lubrication to description of tribological systems.
They realized that the elastohydrodynamic lubrication can exist in the transition region from the boundary to the hydrodynamic lubrication and that the thickness of the lubricating film can vary in response to the conditions. Thus, the elastohydrodynamic theory was supplemented with the concept that a lubricated load-carrying system could theoretically functions in case of different friction mechanisms, from boundary (fine filmed) to mixed (film), from elastohydrodynamic to hydrodynamic (full film) in response to the operating conditions (load, speed, temperature), the geometry of rubbing surfaces, the characteristics of and load-carrying ability of tribosystems.
L. Dintenfass and then R.I. Tanner used the main concepts from this paper and endeavored to find a more sound proof of applicability of the elastohydrodynamic theory to explanation of mechanism of lubrication of joints [12]. They approached the problem from the analytical viewpoint and calculated the synovial fluid viscosity and lubricating film thickness using the equation of classic hydrodynamics as the latest elastohydrodynamic theory. They analyzed discrepancy between the calculation and experimental results and formed the idea the elastohydrodynamic model of lubrication of joints is most probable. Moreover, Dintenfass assumed that elastic deformation of the cartilage together with the viscoelastic properties of the synovial fluid increase the contact area of the articular surfaces and maintain thus its larger load-carrying ability. However, irrespective of the importance of the postulates of the elastohydrodynamic theory of lubrication of joints and primarily those relating to the viscoelastic behavior of articular surfaces in the dynamic contact, P. Marnell and R.K. White providing later a proof evidencing that no pure elastohydrodynamic lubrication of joints can ever exist [13]. In other words, the elastohydrodynamic theory of lubrication of joints , like the hydrodynamic theory in its time, was put under doubt and did not gain any confirmation.
Other researchers doubted too that the film lubrication of joints could exist. J. Charnley put under doubt in the late 50 s experimentally obtained the data that Jones obtained about the exponential pattern of attenuation of pendulum oscillations during friction in the interphalangeal joint proving in favor of the film lubrication in the load-carrying unit. Referring to his own experimental results with the pendulum workbench, he demonstrated in particular that the amplitude of pendulum oscillations as a load-carrying unit of the shinbone joint recedes in time fully linearly rather than exponentially. Hence, it evidences the boundary lubrication of the joint in the pendulum workbench that he demonstrated in particular [11]. Charnley tried to explain the exponential results of Jones by the specific features of his experiments in which an intact joint was instead of a sectioned joint block, so the connective tissues influenced the pattern of attenuation of pendulum oscillations.
C.H. Barnett and A.F. Cobbold later studied this problem more exhaustively. Using the shinbone joints of a dog as load-carrying units they demonstrated that the ligaments and tendons were intact, while the amplitude time characteristics had really an exponential form [11, 14, 15]. When the ligaments and tendons were sectioned, the dependence of the amplitude on time would become linear.
The results fully confirmed the reasoning of Charnley about the effect of the connective tissues of joints on the pattern of attenuation of pendulum oscillations, on the one hand, and quite convincingly prove the assumption that boundary friction can occur in the joints, on the other hand. He believed that it was confirmed by the fact the synovial fluid had the friction coefficient that remained low until the sliding velocity of the rubbing surfaces was very low or nearly zero. Hence, in opposition to the hydrodynamic theory with it main parameter being the viscosity of the synovial fluid, Charney supported the theory of boundary lubrication of joints and believed that another as important parameter was the lubricity or “oiliness” of the synovial fluid alongside with configuration and the quality of rubbing cartilaginous surfaces [7].
In other words, Charney insisted on domination of the boundary lubrication over the hydrodynamic thus assuming that exactly it was the main mechanism providing effective functioning of the joints. Still, he and other researchers admitted that the deformability of articular cartilages plays in all probability a quite essential role in the mechanism of their lubrication together with the fact that this mechanism was most probably intricate or complex [7].
Subsequent experiments with pendulum tribometers confirmed justness of earlier obtained linear amplitude-time dependencies both for animal and human joints. It is shown in [11, 15] that the human hip joint would demonstrate similar regularities as a load-carrying support of the pendulum. Whence it was concluded that the mechanism of boundary lubrication governs the functioning of the human hip joint. Besides, it was also conjured that the cartilage surface layer rich in lipids created this mechanism. Since the studies of dissected joints with the pendulum would invariable yield linear dependences [14, 15], it led to the conclusion that the mechanism of boundary rather than film lubrication was effective in this case.
However, Barnett doubted it in 1962 and showed replaced of the animal joint with a hydrostatic bearing with a liquid film created beforehand would also yield a linear pattern of the ratio between the amplitude of oscillations and time [11, 14, 15]. Moreover, he determined that growth of loading reduces the friction coefficient, as it should have been expected in case of film lubrication. The authors [11] made the same conclusion when they analyzed the equation charactering the motion of the pendulum load-carrying unit as the coulomb one, i.e. as constant typical in the lubrication, on the other hand, and responsive to the viscous resistance determined only by the rheological properties lubrication. Proceeding from their assumptions about the possibility of the lubrication film of regular thickness over the entire contact of the joint head, they calculated a very low viscous resistance. It followed that its effect in the in the load-carrying unit on the exponential pattern of attenuation of pendulum oscillations would be so little manifest that very sensitive instruments are necessary to register it. In other words, it is possible that any effect of viscous forces can remain undetected by the system measuring the amplitude of pendulum oscillations. Therefore, a conclusion was made that the obvious linear type of the pendulum amplitude -time dependencies should not indicated obligatorily the mechanism boundary of lubrication in the load-carrying unit, specifically if other types of lubrication are probable too [11, 15].
However, oppositely to the preceding calculations, S.A.V. Swanson used the assumption about the possibility of fully film lubrication proved theoretically that to explain the observable characteristics of friction in real joints the synovial fluid viscosity should be 100–1000 times than any other its known value [15]. From this fact, he concluded that the lubrication of joints was predominantly boundary, though admitted some possible share of the film mechanism.
Thus, the majority of authors who used the pendulum friction machine in their experimentx share the view about the mechanism of lubrication of joints believing it predominantly boundary by nature.
Meanwhile, other researchers who used the reciprocating friction machines believed that the major role in the functioning of human and animal joints belonged to the liquid film lubrication [7]. Hence, new theories of lubrication of joints were advanced based on the regularities typical for hydrostatic friction, unlike the hydrodynamic or elastohydrodynamic lubrication. An essential role was attributed to the interstitial fluid that is known to make up a considerable portion (up to 60–80 %) of the intercellular substance of the cartilage matrix. The role in the mechanism of motion of joints remained long a subject of debates [10]. Already in 1904, R. Fick considered that the articular cartilage deformed and its volume thus did not change at all. Hence, the cartilaginous tissue secreted no fluid. However, some time later a different point of view appeared according to which the changes in the cartilage in the process of motion caused alternating compression and decompression that favored transfer of the interstitial fluid. The ability to exude and absorb the fluid was also studied by Beninghoff who investigated the cartilage elasticity in his series of experiments [7]. However, the properties of exudation and absorption were known long ago and nobody but C.W. McCutchen emphasized the fact that these properties might play an essential role in the mechanism of lubrication of synovial joints [5, 7].
4.2 Conceptual Models of Joints Lubrication
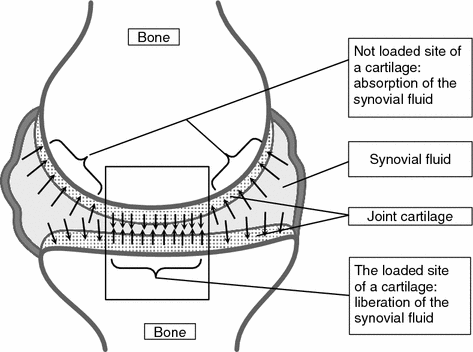
McCachen in 1959 used a system in which rubbing materials were cartilage and glass and demonstrated that after each period of fluid the friction coefficient between them would drop significantly. In case absorption was suppressed and its concentration in the cartilage would reach the ultimate minimum, the friction coefficient would grow strongly reaching 0.35. Therefore, he assumed that lubrication of synovial joints resulted from secretion of the interstitial fluid when the cartilaginous tissue was compressed. McCachen used the term “effusion lubrication” (“weeping lubrication”) to describe the system in which the cartilage released the interstitial fluid and created hydrostatic pressure maintaining contact at a microscopic distance and favoring in this way the general mechanism of lubrication of joints [7].
It is assumed in the theory of lubrication by effusion that the synovial fluid moves between cartilage surfaces and in cartilaginous bodies proper like a compressible fluid (Fig. 4.2).
In other words, according to [7], when the dynamic contact affects mutually rubbing articular surfaces the contact bears the hydrostatic pressure of the fluid exuded by the cartilaginous tissue, therefore, no friction appears. This interpretation of the theory of lubrication by effusion enabled for the first time to explain soundly the low friction in the joints, in particular when rubbing cartilaginous surfaces ceased to move one in respect of another. However, notwithstanding the positive aspect of this theory, the problem if the cartilaginous tissue would exude enough fluid to produce a liquid film thick enough for the joints to function effectively sprang up to be debated so far.
While admitting the role of the cartilage and synovial fluid in lubrication of joints, new modern structural methods stimulated further interest of researchers to investigate the functional anatomy of articular tissues. Considerable progress of scanning electron microscopy in mid 60 s enabled to penetrate into the ultrastructural characteristics of the articular cartilage and general morphological concepts issued [16]. More detailed studies illustrated that the surface layer of the cartilage matrix differs by its structure and properties remarkably from other subsurface zones. Most of the researchers, in their turn, began to attribute to it an essential role in lubrication of joints [17]. C. Weiss made as important assumption in 1968 that the cartilage surface layer acted as a membrane [18]. Other authors shared this concept then after evaluating the studies of the chemical and morphological characteristics of the articular cartilage. This concept asserts the surface layer of the cartilage matrix is highly permeable for water, nutritive substances, and some other compounds with low molecular weights [19–21]. It was concluded that migration of fluid between the synovial cavity and articular cartilage was essential in the process of lubrication and nutrition of the joint cartilage.
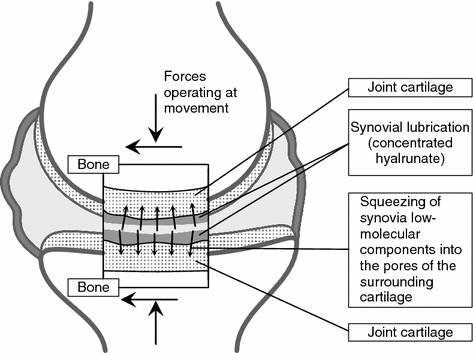
The data about the morphological, chemical, physical, and mechanical properties of the cartilage and synovial fluid emerged in late 60 s gave rise to new theories of lubrication of joints. The essential role played primarily the observations showing that: 1—the cartilage surface can adsorb the hyaluronic acid from the synovial fluid and produce the required protective layer in the process of functioning of the [22, 23]; 2—the synovial fluid viscosity can change in response to the shear rate and pressure on the articular contact; 3—the compliant cartilage contact can support the compressible liquid film (Fig. 4.3), so that when it approaches the articular surfaces its thickness may reach an order of tens of micrometer so that the rubbing surfaces become almost fully separated.
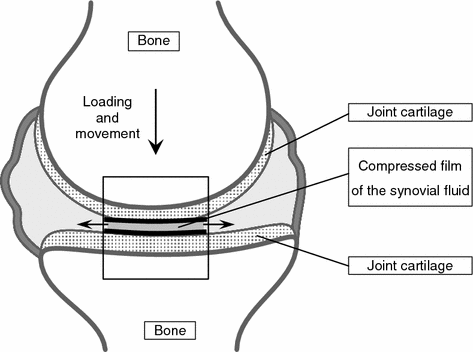

Fig. 4.3
Diagram of mechanism of joint by “compressed liquid film” («squeezed film lubrication») [24]
P.S. Walker with colleagues published in the late 60 s a number of articles. They studied cartilaginous hyaline specimens dried by freezing using the SAM method and established that the synovial fluid was entrapped and arrested between projections on the cartilage surface [25, 26]. They reported that the liquid film thickness ranged from 0.25 to 10 µm [26, 27].
Accordingly, the fluid viscosity was calculated theoretically under the preset experimental conditions and it was established that this parameter in the contact between the synovial fluid and the cartilage had much higher values than inside the fluid. This was also postulated in the experimental friction studies. More profound studies of the effects demonstrated that compression of the lubricating film would intensify during a longer period of time [28]. A conclusion followed from the studies that the synovial fluid was trapped during functioning of the joints, and then it would concentrate or enrich by squeezing of its low-molecular components into the pores of the surrounding cartilage (Fig. 4.4).
Thus, Walker and other researchers proposed a new explanation of the mechanism of lubrication of joints stating that the molecular structure of the synovial fluid, its elasticity, porosity, and characteristics of the articular cartilage contact favor longer existence of separating contact-lubricating films [25, 28]. These lubrication types are known as “reinforced or “boosted” lubrication .
It is believed that, when articular cartilages come into contact, the spaces between surface projections on cartilaginous bodies entrap the synovial fluid, squeeze the low-molecular components through the pores of the matrix of cartilaginous bodies boosting the concentration of high-molecular components and the synovial fluid viscosity in the compressed film, hence, the joints are better able to carry the loading.
Thus, even a cursory comparison of the theory of boosted lubrication and the theory of lubrication by effusion shows that there is a distinct difference between these two postulated type lubrication of joints. It is true that lubrication by effusion requires secretion of the interstitial fluid, boosted lubrication needs just the opposite—fluid absorption by the cartilage when it loaded in the process of motion, i.e. these two types of lubrication of joints seem to exclude one another.
Trying to resolve this contradiction between two types of lubrication, F.C. Linn proposed a new joint cartilage model using the known mechanical and физичecкиx properties and the results obtained with the SAM about the cartilaginous tissue ultrastructure [15]. This model of the synovial type joint includes two porous elastic disks from a composite material under compression that a fluid film separates. The composite material can absorb and release the fluid through its surface providing resistance in elongation or compression, while it retains still substantial non-linearity. If it is assumed that τ—a dimensionless time parameter вpeмeни, ρ—the radial measure in the cartilage, Ψ and Φ—pressure in the articular cartilage and pressure in the fluid, then the fluid flow through the joint cartilage surface is proportional to the difference between these pressures, i.e. Ψ–Ф.
According to parametric solution of Linn for this system, the synovial joints demonstrate two types of lubrication in response to period of time (Fig. 4.5). Initially (τ = 0) the fluid flow characterized by the value Ψ–Φ goes from the clearance into the cartilaginous bodies in their middle zone; the external circular region shows a reverse pattern, i.e. cartilaginous bodies are compressed in the initial period, the fluid is absorbed in the central part of the cartilage contact and released through the pores over their periphery. Linn notes that this situation persists during the next period too (τ = 3). However, in the later period (τ = 6), as compression of the cartilaginous bodies accumulates, the fluid flow is fully directed from the cartilaginous bodies into the clearance between them.
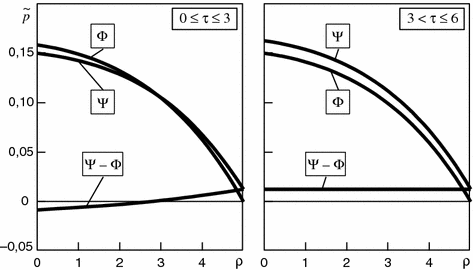

Fig. 4.5
Dimensionless pressure in fluid film Φ and model cartilage Ψ as function of radius ρ
According to many works, both the mechanism of boosted lubrication and that of lubrication by effusion are active because the fluid circulates in the contact region in reciprocating directions between the clearance and the cartilage bodies. After some time an asymptotic condition of the self-regulating hydrostatic mode sets and only the mechanism of lubrication by effusion remains active, i.e. the fluid flow proceeds only in direction, namely, the cartilaginous bodies into the intermediate clearance.
Thus, Linn used the obtained data employing model ideas about joints of the synovial type in order to compromise the theories of boosted lubrication and lubrication by effusion in joints.
Nevertheless, a number of researchers continued to believe that that the precise manner by which the fluid film appeared between cartilage surfaces, did not conform the hypothesis of McCuchen about lubrication by effusion or the postulate of Walker about the booster mechanism [10, 29]. The following facts evidenced in favor of these statements. On the one hand, a number of publications [22, 30, 31] note that decomposition of the hyaluronic acid was due to the selective effect of hyaluronidase on the synovial fluid so that would lose its thixotropic properties and its viscosity would approach to that of water without influencing the tribological properties of cartilaginous surfaces. That put naturally the main postulates of the theory of boosted lubrication of joints under doubt. On the other hand, the analytical studies of transitional oscillatory processes in dynamic joint motion under the effect of a fixed normal load on the laminar porous, permeable elastic medium demonstrated that McMuchen’s forms of lubrication by effusion could be most probable only in the case if the joint did not slide. At the same time, simulation of the process sliding of the synovial joint after the motion stabilized under normal loading in the contact similarly to the laminar porous and elastic system enabled to determine that, when the properties of materials corresponded to those of the healthy cartilage and subcartilage bone substances, the interstitial fluid exudes over the traveling loading front and absorbs in joint cartilage contact in front and behind of the traveling loading rear line [10]. Other authors observed the same flow field too. The assumption ensued that the natural mechanism of lubrication of normal joints was conditioned by the circular fluid flow over the rubbing articular surfaces.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree