(1)
where
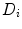 is a diffusion parameter dependent on the total extracellular matrix density (ECM)
is a diffusion parameter dependent on the total extracellular matrix density (ECM) 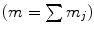 ,
, 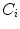 are advection coefficients representing chemo- and haptotactical movement controlled by growth factor concentrations and ECM densities. The index
are advection coefficients representing chemo- and haptotactical movement controlled by growth factor concentrations and ECM densities. The index 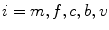 indicates the different cell types, stem cells, fibroblasts, chondrocytes, osteoblasts and endothelial cells, respectively. Furthermore, proliferation, differentiation and apoptosis are realized by reactive terms
indicates the different cell types, stem cells, fibroblasts, chondrocytes, osteoblasts and endothelial cells, respectively. Furthermore, proliferation, differentiation and apoptosis are realized by reactive terms 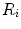 , which are regulated by the biochemical milieu, i.e. matrix densities and growth factor concentrations.
, which are regulated by the biochemical milieu, i.e. matrix densities and growth factor concentrations.The tissue development inside the callus is given by four extracellular matrix densities 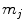 , where
, where 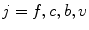 denotes fibrous, cartilage, immature bone and vascular tissue, respectively. The production and, in case of connective tissue and cartilage the resorption, is represented by reaction equations
denotes fibrous, cartilage, immature bone and vascular tissue, respectively. The production and, in case of connective tissue and cartilage the resorption, is represented by reaction equations
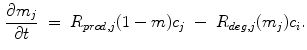
Here again 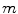 denotes the total tissue density. Unlike the original model, where each tissue growth was capped by its individual local density through the term
denotes the total tissue density. Unlike the original model, where each tissue growth was capped by its individual local density through the term 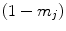 , a competition between the growing tissues was implemented by using the
, a competition between the growing tissues was implemented by using the 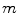 in this case. Growth factors taking part in bone repair are grouped into osteogenic, chondrogenic and angiogenic growth factor concentrations. These concentrations, indicated by index
in this case. Growth factors taking part in bone repair are grouped into osteogenic, chondrogenic and angiogenic growth factor concentrations. These concentrations, indicated by index 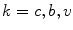 , are given by diffusion-reaction equations of the form
, are given by diffusion-reaction equations of the form
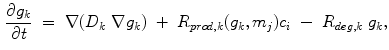
where 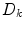 is the diffusion coefficient and
is the diffusion coefficient and 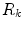 are production and degradation terms. Growth factor production depends on the biochemical milieu and the respective cell populations
are production and degradation terms. Growth factor production depends on the biochemical milieu and the respective cell populations 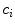 .
.
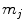 , where
, where 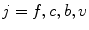 denotes fibrous, cartilage, immature bone and vascular tissue, respectively. The production and, in case of connective tissue and cartilage the resorption, is represented by reaction equations
denotes fibrous, cartilage, immature bone and vascular tissue, respectively. The production and, in case of connective tissue and cartilage the resorption, is represented by reaction equations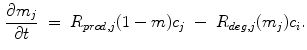
(2)
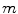 denotes the total tissue density. Unlike the original model, where each tissue growth was capped by its individual local density through the term
denotes the total tissue density. Unlike the original model, where each tissue growth was capped by its individual local density through the term 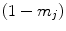 , a competition between the growing tissues was implemented by using the
, a competition between the growing tissues was implemented by using the 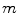 in this case. Growth factors taking part in bone repair are grouped into osteogenic, chondrogenic and angiogenic growth factor concentrations. These concentrations, indicated by index
in this case. Growth factors taking part in bone repair are grouped into osteogenic, chondrogenic and angiogenic growth factor concentrations. These concentrations, indicated by index 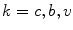 , are given by diffusion-reaction equations of the form
, are given by diffusion-reaction equations of the form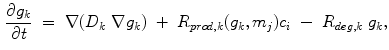
(3)
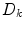 is the diffusion coefficient and
is the diffusion coefficient and 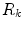 are production and degradation terms. Growth factor production depends on the biochemical milieu and the respective cell populations
are production and degradation terms. Growth factor production depends on the biochemical milieu and the respective cell populations 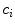 .
.2.1 Mechanical Stimulation
An isotropic hyperelastic material law is used for the callus region, assuming a nearly incompressible material for the soft tissues. As a measure for local mechanical demand 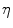 within the callus the equivalent deviatoric strain
within the callus the equivalent deviatoric strain 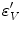 is used
is used
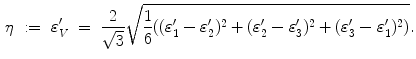
The level of mechanical excitation 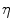 then defines stimuli parameters
then defines stimuli parameters 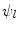 , with
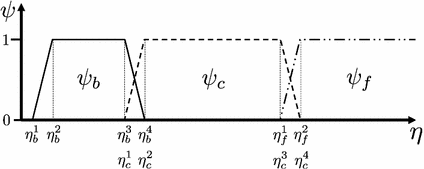
, with 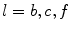 denoting osteogenic, chondrogenic and fibrogenic stimulation, as indicated in Fig. 1. The parameters
denoting osteogenic, chondrogenic and fibrogenic stimulation, as indicated in Fig. 1. The parameters 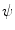 take on values between
take on values between 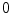 for no and
for no and 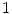 for a maximal stimulation.
for a maximal stimulation.
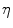 within the callus the equivalent deviatoric strain
within the callus the equivalent deviatoric strain 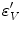 is used
is used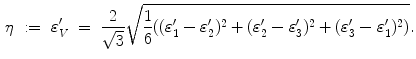
(4)
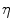 then defines stimuli parameters
then defines stimuli parameters 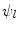 , with
, with 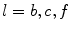 denoting osteogenic, chondrogenic and fibrogenic stimulation, as indicated in Fig. 1. The parameters
denoting osteogenic, chondrogenic and fibrogenic stimulation, as indicated in Fig. 1. The parameters 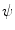 take on values between
take on values between 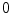 for no and
for no and 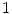 for a maximal stimulation.
for a maximal stimulation.
Fig. 1
Definition of stimulation parameter 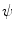 by mechanical excitation levels
by mechanical excitation levels 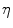
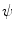 by mechanical excitation levels
by mechanical excitation levels 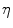
The implementation of the stimulations 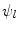 is presented for the stem cell equation,
is presented for the stem cell equation,
![$$\begin{aligned} \frac{\partial c_m}{\partial t}&=\ \nabla [D_m\nabla c_m -\ C_m(\nabla g_b, \nabla g_v, \nabla m)c_m]\ +\ A_mc_m(1-c_m)\nonumber \\&\quad -\ (\psi _b F_1\ + \psi _c F_2\ +\ \psi _f F_4)c_m. \end{aligned}$$](/wp-content/uploads/2016/10/A324942_1_En_3_Chapter_Equ5.gif)
Here 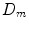 ,
, 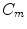 are diffusive and advective coefficients as above,
are diffusive and advective coefficients as above, 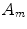 denotes the proliferation parameter and
denotes the proliferation parameter and 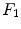 ,
, 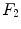 and
and 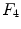 are the differentiation coefficients for osteogenic, chondrogenic and fibrogenic differentiation. By multiplication of
are the differentiation coefficients for osteogenic, chondrogenic and fibrogenic differentiation. By multiplication of 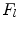 with the respective
with the respective 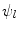 the intensity of the differentiation is scaled.
the intensity of the differentiation is scaled.
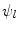 is presented for the stem cell equation,
is presented for the stem cell equation,![$$\begin{aligned} \frac{\partial c_m}{\partial t}&=\ \nabla [D_m\nabla c_m -\ C_m(\nabla g_b, \nabla g_v, \nabla m)c_m]\ +\ A_mc_m(1-c_m)\nonumber \\&\quad -\ (\psi _b F_1\ + \psi _c F_2\ +\ \psi _f F_4)c_m. \end{aligned}$$](/wp-content/uploads/2016/10/A324942_1_En_3_Chapter_Equ5.gif)
(5)
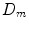 ,
, 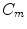 are diffusive and advective coefficients as above,
are diffusive and advective coefficients as above, 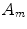 denotes the proliferation parameter and
denotes the proliferation parameter and 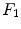 ,
, 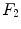 and
and 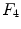 are the differentiation coefficients for osteogenic, chondrogenic and fibrogenic differentiation. By multiplication of
are the differentiation coefficients for osteogenic, chondrogenic and fibrogenic differentiation. By multiplication of 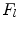 with the respective
with the respective 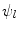 the intensity of the differentiation is scaled.
the intensity of the differentiation is scaled.3 Methods
To solve the presented mathematical model the Finite Element method is employed. However, when a standard Galerkin approach is chosen, spurious oscillations often pollute the solutions of advection-diffusion-reaction equations. These oscillations occur in the vicinity of steep gradients in the solution, which are present from the beginning of the calculation (e.g. at Dirichlet boundaries) or build up during the calculation. Dominance of the advection or reaction terms often lead to steep gradients in the solution. This problem is well documented in literature and various techniques were developed to prevent oscillations.
In this work the Time Discontinuous Galerkin method (TDG) was combined with the finite calculus scheme (FIC) developed by Oñate [13, 14] to achieve a stable solution of the system of instationary advection-diffusion-reaction equations described above, for details it is referred to [11].
3.1 Simulation
As a geometrical model for the simulation a simplified axisymmetric representation of an osteotomy is chosen, as shown in Fig. 2. The dimensions of the callus region are chosen according to [4] to indicate a sheep metatarsal model. The fracture gap is set to 3 mm throughout the presented simulation.
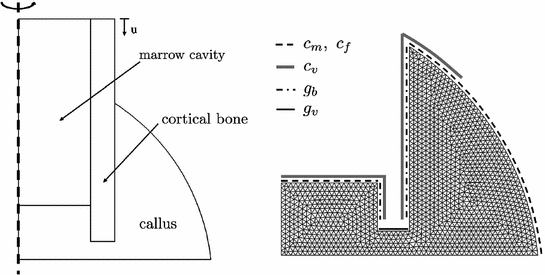

Fig. 2
Axisymmetric representation of sheep metatarsal fracture site (left), meshed callus region with indication of boundary conditions for cell and growth factor reserviors in the surrounding tissue (right)
The boundary conditions for biochemical simulation are shown on the right side of Fig. 2. They describe cell and growth factor reserviors in the surrounding tissue. Stem cells and fibroblasts are therefore recruited from the marrow cavity and soft tissue outside of the periosteal callus. Endothelial cells originate from the periosteum, endosteum and marrow. The source for chondrogenic growth factors is the fractured bone end and osteogenic growth factors invade the callus region from the periosteum and endosteum. The initial condition of the callus is chosen to be a connective tissue of low density, indicating the granulation tissue formed during the inflammation phase of bone healing. And a high concentration of angiogenic growth factor is present throughout the callus in accordance with observations documented in literature [15].
The mechanical simulation is executed at the start of each day of healing. At the beginning of the healing process a maximal displacement acts on the cortical bone. The displacement driven simulation continues until the reaction forces calculated on the upper boundary are equal to the maximal load of a sheep leg (i.e. about 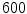 N taken from [12]). Then this maximal force is applied to the former displacement boundary as an axial load and with the stiffening of the callus the interfragmentary movement decreases.
N taken from [12]). Then this maximal force is applied to the former displacement boundary as an axial load and with the stiffening of the callus the interfragmentary movement decreases.
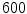 N taken from [12]). Then this maximal force is applied to the former displacement boundary as an axial load and with the stiffening of the callus the interfragmentary movement decreases.
N taken from [12]). Then this maximal force is applied to the former displacement boundary as an axial load and with the stiffening of the callus the interfragmentary movement decreases.Table 1
Mechanical properties of biological tissues
Tissue type | Young’s modulus [MPa] | Poisson ratio |
|---|---|---|
Cortical bone | 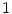 , ,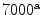 | 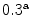 |
Immature bone
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|