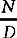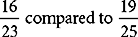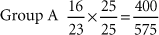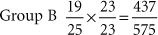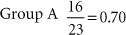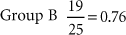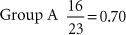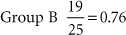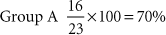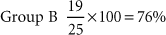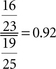RATIOS

When comparisons are made between the proportion of an attribute in two or more groups, the proportions are often expressed as ratios, such as the mortality ratio of persons treated with medical therapy versus those with surgical therapy. Ratios result from the comparison of fractions. Every fraction has a numerator, N, and a denominator, D.

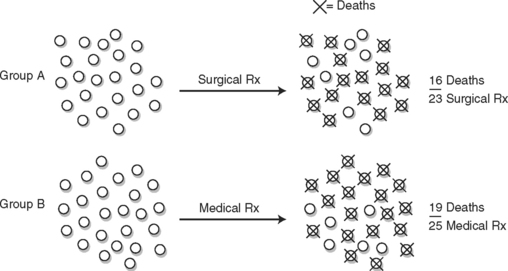
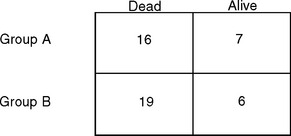
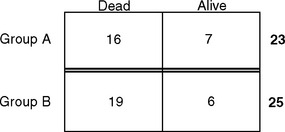
D reflects the number of subjects in the group, such as the number of subjects getting standard medical treatment. N is the number of subjects with the characteristic being measured in the group, such as mortality. Figure 2-1 illustrates the results of a study where subjects with lung cancer received either medical or surgical treatment and mortality rates were compared.

FIGURE 2-1 The mortality rates of each group can be compared using fractions.

It is easier to compare fractions when the denominator of each fraction is the same. This is done by converting the fractions so the denominators are expressed as equal values. Multiplying the numerator and the denominator by the same number does not change the value of the fraction (this is because you are essentially multiplying the fraction by 1). The ratios can be compared by the value of the numerators.

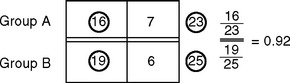
For example, group A had 16 deaths out of 23 individuals in 5 years. Group B had 19 deaths out of 25 individuals in the same time period. Which group fared worse?

This problem is easier to solve if there are equal denominators. We multiply the first fraction by 25/25 and the second fraction by 23/23 to convert to equal denominators, without changing the value of the individual fractions.

Group B did worse; they had a higher death rate.

Another way to compare ratios is to reduce each fraction so that the denominator is equal to 1. Any numerator over a denominator of 1 equals itself. (It follows that any number is actually itself divided by 1.) Do this by dividing the numerator by the denominator. When all fractions in a group are reduced so that their denominators are equal (such as 1 or 100), it is legitimate to compare numerators.

Again, we see that group B had a higher mortality rate.

Fractions can also be expressed as percentages. This implies that the denominators have all been converted to 100. It is easy to compare relative values using the percentage scale, since our currency is based on 100 and all of us know how to compare prices!

Group A had a 70% mortality rate, whereas Group B had a 76% mortality rate.

We can combine the mortality rates for two groups into one number known as a ratio. The mortality rate of one group becomes the numerator, N, and the mortality rate of the other group becomes the denominator, D. Both the numerator and denominator are fractions in themselves. For our purposes, when one fraction is divided by another, this will be designated by a double line. Dividing the two mortality rates results in a single number, the mortality ratio.

It is not always apparent which group was designated to be in the numerator and which was designated as the denominator. If the result is less than 1, we know that the mortality rate of the group represented in the numerator was less than the other group, but we often need to rely on an explanation in the text to identify exactly which group fared better.

2 × 2 TABLES

One common method of displaying the data that measures the prevalence of a characteristic in each of two groups is a chart known as a 2 × 2 table. These tables can be confusing at first glance because it is intuitive to give the four boxes equal emphasis, but actually they should be interpreted in a sequence. For the above example, the cells hold the number of subjects who died versus those remaining alive after the study period.

First, identify the groups being compared by imagining a double line. We need to add the rows the get the total number in each group. These will be the denominators.

Then identify the numerator, which is the characteristic being measured. This example is comparing mortality rates, so the number of deceased subjects for each group will be the numerators.

The 2 × 2 table is extremely common. Like the basic black dress, it is ideal for many different situations. (It is very simple in construction, yet elegant in the way it shows off its figures!) There are several applications of this type of data display, and you will undoubtedly encounter this table many times. Remember to interpret these data by first identifying the groups or denominators.

LOGIC AND VENN DIAGRAMS

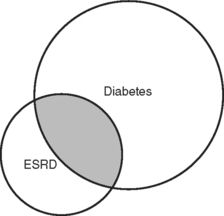
Certain groups of individuals tend to have associated characteristics. For instance, people with diabetes tend to have end-stage renal disease (ESRD) requiring dialysis. But not all people on dialysis have diabetes, and not all diabetics have renal failure. These relationships can be expressed graphically as Venn diagrams, where one circle represents condition 1 and another circle represents condition 2. An example of a Venn diagram is shown in Figure 2-2. These are rough diagrams that do not have numerical meaning, but the relative sizes of the circles are often a crude estimate of the relative prevalence of the conditions. The overlap represents those subjects with both conditions.

FIGURE 2-2 The crude relationship between diabetes and ESRD. We see that the prevalence of diabetes is higher than ESRD, and that roughly half of those with ESRD have diabetes.

(After Arkey, R. A., consulting ed. 2001. MKSAP 12: Nephrology and hypertension. Philadelphia: American College of Physicians-American Society of Internal Medicine).

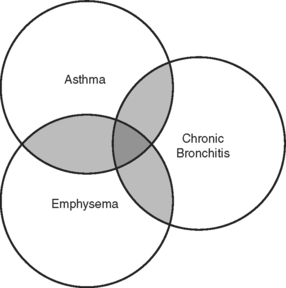
Venn diagrams do not need to be limited to two conditions. For example, Figure 2-3 illustrates the relationship between asthma, chronic bronchitis, and emphysema. Some people have just one of these conditions, others have two, and the ones represented in the middle of the diagram have been diagnosed with all three. This Venn diagram also illustrates that none of these conditions is exclusive. The presence of one condition does not exclude the possibility of having another.