(1)
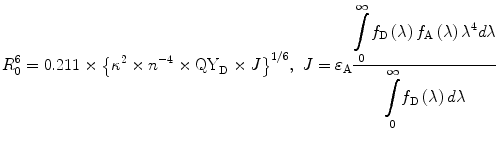
(2)
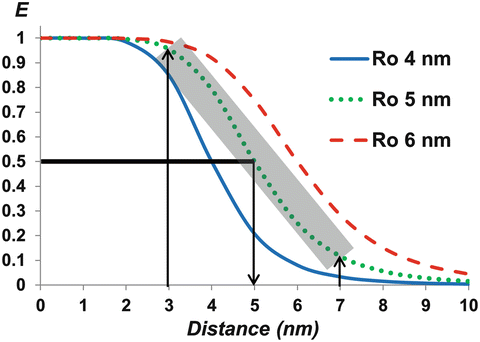
Fig. 1
FRET efficiencies (E) versus the separation distance between the donor and the acceptor (r), based on Eq. 1, for a Förster distance (R 0) of 4, 5, or 6 nm, at which E is 50 %. Due to the dependence on the sixth power of the donor-acceptor distance, E is very sensitive to the distance change around R 0—as an example highlighted for the R 0 of 5 nm, the E values fall sharply for the distance increase from 3 nm to 7 nm
Using FLIM, FRET events can be identified by measuring the reduction in the donor lifetime that results from quenching in the presence of an acceptor, and E can be estimated from the donor lifetimes determined in the absence (τ D—unquenched lifetime) and the presence (τ DA—quenched lifetime) of the acceptor, as shown by Eq. 3 [11].
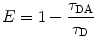
Since only donor signals are measured for determining E in FLIM-FRET, the method does not usually require the corrections for spectral bleedthrough that are necessary for intensity-based FRET measurements of the sensitized emission from the acceptor [20–24]. The fluorescence lifetime is insensitive to changes in fluorophore concentration, excitation light intensity, or light scattering but sensitive to environmental changes—these facts make FLIM-FRET an accurate method for FRET measurements. The FLIM-FRET method has been routinely applied in many laboratories including ours for studying Protein–Protein interactions and investigation of signaling events in a variety of biological systems [9, 25–46].
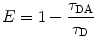
(3)
1.3 Overview of FLIM Techniques
FLIM techniques are generally subdivided into time-domain (TD) and frequency-domain (FD) methods. The basic physics that underlie the two methods is essentially identical, since they are finite Fourier transforms of each other. In TD FLIM, a fluorophore is excited by a pulsed light source, which is synchronized to high-speed detectors and electronics; its fluorescence decay profile is directly measured in a number of (at least two) sequential time bins after (and relative to) the excitation pulse (time zero); its fluorescence lifetime can be estimated by analyzing the recorded decay profile (Fig. 2a). In FD FLIM, a modulated light source is used to excite a fluorophore, whose emission signals are measured by a detector modulated either at the same modulation frequency of the excitation (homodyne) or at a slightly (a few hundred to thousand hertz) different frequency (heterodyne); analyzing the phase shift(s) and amplitude attenuation(s) of the emission relative to the excitation makes it possible to extract the fluorescence lifetime of the fluorophore (Fig. 2b). The repetition rate of the excitation source used in TD FLIM or the fundamental modulation frequency of the excitation source used in FD FLIM needs to be chosen according to the fluorescence lifetime to be measured. The rate or frequency for measuring nanosecond lifetimes in most biological applications should be on the megahertz scale, e.g., 10–100 MHz.
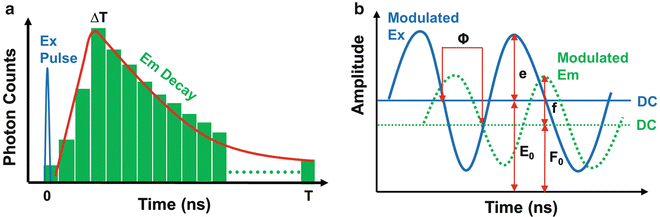

Fig. 2
The fundamental principles of time-domain (TD) and frequency-domain (FD) FLIM measurements. (a) TD FLIM usually employs a pulsed light source that is synchronized to high-speed detectors and electronics to measure the emission (Em) signals at different time bins relative to the excitation (Ex) pulse (time zero), directly producing a fluorescence decay profile; the fluorescence lifetime is estimated by analyzing the recorded decay profile. (b) FD FLIM typically uses modulated light sources and detectors and measures the phase shift Φ and the amplitude attenuation M {M = (f/F 0)/(e/E 0)} of the emission relative to the excitation, which are then analyzed to estimate the fluorescence lifetime
Many TD and FD FLIM techniques were developed and demonstrated for various biological applications. Fortunately, most of them are now commercially available, e.g., from Becker and Hickl (BH, www.becker-hickl.de), Picoquant (www.picoquant.com), ISS (www.iss.com), Lambert Instruments (www.lambert-instruments.com), and Intelligent Imaging Innovations (www.intelligent-imaging.com). These systems can be stand alone or integrated with existing widefield or confocal or multiphoton (MP) microscopy systems. Each FLIM technique has its own strengths and limitations and choosing the most suitable one is really dependent upon the biological investigation at hand. Several FLIM techniques are compared in Table 1.
Table 1
Comparison of several commonly used FLIM techniques
FLIM detection | Typical implementation |
|---|---|
Time-correlated single-photon counting (TCSPC) TD FLIM | TCPSC [47] is typically implemented on laser scanning microscopes using a pulsed single- or multiphoton laser, a fast PMT or APD detector (timing jitter <300 ps), and TCSPC electronics [5, 30, 48, 49]. The TCSPC device synchronizes the detector and the scanning clock to the excitation pulse and records the arrival time and spatial information for each detected photon. Accumulating photons for thousands or millions of excitation pulses, a “photon counts” histogram (fluorescence decay profile) for estimating the fluorescence lifetime can be built at each pixel (or voxel) of a 2D (or 3D) image. A multichannel PMT module has also been employed in TCSPC FLIM to obtain spectrally resolved lifetimes [34, 50] |
Gated image-intensified camera TD FLIM | The gating-camera FLIM is typically implemented on widefield and spinning-disk confocal microscopes using a single-photon pulsed laser, a gated image-intensified camera, and gating-control electronics. The gating-camera can be operated at a superfast speed to detect photons within a time (gating) window for a few hundred picoseconds to a few milliseconds relative to the excitation pulse [5, 27]. A number of images are acquired in sequential gating windows to estimate the lifetimes. Extracting single-component lifetimes requires collecting two gated images at minimum, which may only take a few seconds [6, 51]. Due to the fast data acquisition speed, the gating-camera FLIM was implemented in a high-content screening platform [45, 52] |
Streak camera TD FLIM | A streak-camera system, consisting of a streak scope and a fast CCD camera, can be operated to transform the temporal profile of a light pulse into a spatial profile on a detector by causing a time-varying deflection of the light across the width of the detector [53]. In streak-camera FLIM, each line of an image consists of the time resolved information for a pixel location along the X-axis and a series of images are acquired for the Y-axis. The streak-camera FLIM uses a pulsed laser that is synchronized to a streak-camera system and was implemented on MP laser scanning microscopes [29, 31, 53]. Using a spectrograph device, the streak-camera FLIM was also demonstrated to obtain spectrally resolved lifetimes [31] |
Heterodyne digital FD FLIM | In traditional heterodyne FD FLIM, both the light source and the detector are modulated, but at a slightly different frequency, e.g., a few hundred hertz. The recently developed digital FD FLIM employs a modulated pulsed excitation source (one- or multiphoton laser), but does not modulate the detector at all, making the technique much more simpler to implement in laser scanning confocal microscopes [54]. In digital FD FLIM, the detector (PMT or APD) is working in a manner like photon counting, and all operations including the generation of the light modulation frequency, the generation of the cross-correlation sampling frequency, and the assignment of the time of arrival of a photon to a bin are digital, allowing multifrequency measurements (for extracting multicomponent lifetimes) done simultaneously and thus greatly improving photon efficiency and data acquisition speed [46, 54] |
Homodyne FD FLIM using an image-intensified camera | The camera-based FD FLIM is typically implemented in widefield or spinning-disk confocal microscopes, using an LED or diode laser excitation light source and an image-intensified camera, both modulated at the same frequency (homodyne) [55–57]. This FLIM method is very fast since only several images need to be acquired to obtain one lifetime image and this may only take only a few seconds [58] |
1.4 Overview ofFLIM Data Analysis
1.4.1 The General Fluorescent Decay Kinetics Model
In the majority of FLIM measurements, a fluorescent decay is measured from a population of fluorescent molecules. The intrinsic decay kinetics f(t), represented by the numbers of emitted photons as a function of time relative to the excitation, can be modeled by Eq. 4:
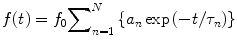
where f 0 is the number of emitted photons at time zero and N (N ≥ 1) is the number of different fluorescent species—each one is associated with a distinct fluorescence lifetime (τ n ), and its percentage over the number of total fluorescent molecules is often termed as the pre-exponential factor (a n ). For a multi-exponential case (N > 1), the apparent lifetime (τ a) calculated by Eq. 5 is often used to indicate the mean lifetime of all fluorescent species.
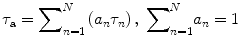
A variety of computer algorithms have been developed for FLIM data analysis [3, 4, 11]. Some are associated with specific FLIM data acquisition methods. For example, the rapid lifetime determination (RLD) algorithm was developed to analyze time-resolved images acquired by a gated image-intensified camera [5, 27, 59]. Some FLIM data analysis strategies vary depending upon the particular biological models. For example, global analysis [60–63] can significantly improve the signal-to-noise ratio (SNR) of fluorescence lifetime images, but the method requires the assumption that identical fluorescence relaxation parameters pertain to the pixels grouped together for analysis, which may not be valid in many experimental systems.
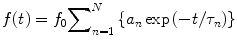
(4)
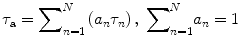
(5)
1.4.2 Fitting Analysis of TCSPC FLIM Data
Fitting analysis is commonly used in both TD and FD FLIM data analyses [11, 64]. In TCSPC FLIM, a measured decay g(t) is typically represented as the convolution of the intrinsic decay f(t) (Eq. 4) and the instrument response function (IRF) of the FLIM system plus noise n(t), as shown in Eq. 6:
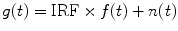
Given the IRF and some a priori parameters of the intrinsic decay, e.g., the number of exponential components (N in Eq. 4), an iterative fitting (deconvolution) procedure is usually applied to estimate the values of each lifetime component (τ n in Eq. 4) and the corresponding pre-exponential factor (a n in Eq. 4). At each iterative step k, an estimated g k (t) is calculated from the convolution of the IRF and the intrinsic decay modeled by the estimated lifetimes and pre-exponential factors; the estimated g k (t) is then compared to the measured g(t) to produce the standard weighted least squares (χ 2), which will be used as a criterion to evaluate the fitting significance and to determine whether or not to stop the iterative fitting procedure. The value of χ 2, indicating a good fit for an appropriate model and a random noise distribution, should be close to 1 predicted by Poisson statistics with enough data points for fitting [11, 64].
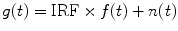
(6)
1.4.3 Model-Free Phasor Plot Analysis of FD FLIM Data
In FD FLIM, the measured data at each pixel is usually composed of both phase delay (Φ) and amplitude modulation ratio (M), as shown in Fig. 2. The lifetime of a single fluorescent species (N = 1 in Eq. 4) can be directly calculated from either the phase (τ Φ—the phase lifetime) or the modulation by Eq. 8 (τ M—the modulation lifetime).
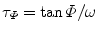
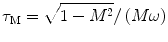
where ω is the modulation frequency. A difference between τ Φ and τ M is an indication that the data does not follow a mono-exponential time course. For a multi-exponential case (N > 1 in Eq. 4), the phase and modulation values are often measured at several modulation frequencies. From low to high frequencies, the phase delays increase from 0 to 90°, while the modulation ratios decrease from 1 to 0. To estimate the values of each lifetime component (τ n in Eq. 4) and the associated pre-exponential factor (a n in Eq. 4), the weighted least squares numerical approach can be used to fit both phase and modulation values measured at different frequencies, given some priori parameters of the exponential model, e.g., the number of exponential components (N in Eq. 4). Similar to TCSPC FLIM data fitting analysis, the calculated χ 2 and residuals provide an evaluation for the fitted results.
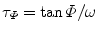
(7)
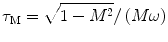
(8)
Other than the fitting analysis, a graphical method for FLIM data presentation and analysis was developed. This method, named as polar plot [65], AB plot [66, 67], or phasor plot [68, 69] by different groups, is essentially based on the transformation of FD FLIM data defined by Eq. 9.
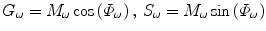
Given a modulation frequency ω, each measured FD FLIM data point (Φ ω and M ω ) can be directly located in a 2D plot using G ω as the horizontal axis and S ω as the vertical axis (Eq. 9). For a single-lifetime species, the phase (Eq. 7) and modulation (Eq. 8) lifetimes are equal, from which a relationship between the G ω and S ω coordinates shown in Eq. 10 can be derived.
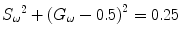
This G ω − S ω relationship is represented as a semicircle curve centering at (G ω = 0.5, S ω = 0) with a radius of 0.5 in the phasor plot. The semicircle curve indicates the lifetime trajectory with decreasing lifetime from left to right, where (1, 0) indicates lifetimes near zero to (0, 0) being infinite lifetime. A point falling on the semicircle will have only a single lifetime, while a point that falls inside the semicircle will have multiple lifetime components.
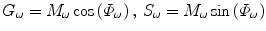
(9)
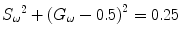
(10)
Since no fitting is involved, the phasor plot approach is independent of any underlying physical model. By plotting raw data in the phasor plot, one can distinguish between single- and multicomponent lifetimes, identify the lifetime value of a single-lifetime species on the semicircle, and also visualize the relative lifetime changes between complex lifetime distributions. More conveniently, many data distributions measured from different samples can be directly compared in a same phasor plot. In FLIM-FRET measurements, FRET can be identified by comparing the phasor plot distributions of the donor fluorophores in the donor-alone versus the “donor + acceptor” specimens. Several analytical tools were developed based on the polar, AB, or phasor plot approach for multicomponent analysis without nonlinear fitting [66, 67] and determining the FRET efficiency [57, 68], e.g., the “FRET Trajectory” functions in the SimFCS software (www.lfd.uci.edu/globals) [68]. It should be noted that these methods can be also employed to analyze raw TCSPC FLIM data after being transformed into the frequency domain through the digital Fourier transform—such a function is provided by the SimFCS software [68].
1.5 Outline of a FLIM-FRET Protocol
A typical FLIM-FRET experiment involves three steps:
1.
Calibrate the FLIM system with fluorescence lifetime standards.
2.
Acquire FLIM data from biological specimens, typically including specimens that only have the donor and from specimens that contain both the donor and the acceptor.
3.
Analyze the data to extract the lifetime information and interpret the analyzed data to illustrate the biological activity or other experimental objectives.
Here, we describe the procedures that are necessary to use both a TCSPC FLIM method and a FD FLIM method to monitor Protein–Protein interactions in live specimens based on FRET. Both synthetic and real biological models are used for FLIM-FRET demonstrations in live cells.
2 Materials
2.1 TPE TCSPC FLIM System
The basic principle of TCSPC FLIM is described in Fig. 2a and Table 1.
1.
The TPE TCSPC FLIM system is implemented on a Bio-Rad Radiance 2100 confocal/MP microscope system using the MP system configuration, which is operated by the Bio-Rad LaserSharp 2000 software (www.zeiss.com/micro). The Bio-Rad scanning unit is attached to a Nikon TE300 inverted microscope.
3.
4.
The TPE laser is a Coherent 10 W Verdi pumped tunable (700–1,000 nm) mode-locked ultrafast (pulse width <150 fs) pulsed (repetition rate of 78 MHz) laser (www.coherent.com).
5.
A remotely controlled filter wheel containing several emission filters is placed before the FLIM detector. The 480/40 nm (for Coumarin 6 and Cerulean) and 525/50 nm (for Fluorescein) emission filters (www.chroma.com) were used.
6.
A Nikon 60X/1.2NA water objective was used for all TCSPC FLIM measurements.
7.
The TCSPC module and FLIM detector are controlled by the BH SPCM software.
8.
The acquired TCSPC FLIM data is analyzed using the BH SPCImage software.
2.2 Measurement of the TCSPC FLIM Instrument Response Function (IRF)
The IRF can be estimated from the acquired decay data itself. However, it is preferable to directly measure the IRF experimentally, e.g., by recording scattered excitation light. For visible light excitation, a strongly scattering specimen such as nondairy coffee creamer is conventionally used to record the IRF [5]. For infrared light excitation, the IRF can be measured using a sample (such as urea crystal) that yields second-harmonic generation (SHG) signals [70]. SHG is a nonlinear process that delivers a signal at one-half of the excitation wavelength.
1.
A thin layer of urea crystal sandwiched between a glass coverslip and a glass slide was used to measure the IRF of the TPE TCPSC FLIM system.
2.3 Confocal FD FLIM System
The basic principle of digital FD FLIM is described in Fig. 2b and Table 1. We use the ISS ALBA confocal digital FD FLIM/FCS system (www.iss.com).
1.
The ISS ALBA FastFLIM system is attached to a Nikon TiE300 inverted microscope.
2.
The excitation source is a Fianium SC450-6 pulsed supercontinuum laser module (www.fianium.com), which covers the excitation wavelengths ranging from 460 to 2,200 nm and has a repetition rate of 60 MHz and a pulse width of 6 ps.
3.
The system is equipped with two identical PerkinElmer SPCM-AQRH-15 avalanche photodiode (APD) detectors (www.perkinelmer.com).
4.
Various combinations of excitation, emission filters, and dichroic mirrors can be configured through the system software. The 445/20 nm (for Coumarin 6, Fluorescein and Cerulean) and 560/25 nm (for Rose Bengal) excitation filters and the 480/40 nm (for Coumarin 6 and Cerulean), 531/40 nm (for Coumarin 6 and Fluorescein), and 630/92 nm (for Rose Bengal) emission filters (www.semrock.com) were used.
5.
A Nikon 60X/1.2NA water objective was used for all FD FLIM measurements.
6.
The phase shifts and modulation attenuations of the emission relative to the excitation at three frequencies (60, 180, 300 MHz) are simultaneously measured at each pixel of a fluorescence lifetime image.
7.
The ISS VistaVision software is used for data acquisition and analysis.
2.4 Fluorescence Lifetime Standards for FLIM System Calibration
Prior to any scientific investigation, a FLIM system must be calibrated with standard fluorophores of known lifetimes. Many of them have been used for calibrating FLIM systems, and a few commonly used ones are given in Table 2. The following standards were used for calibrating our FLIM systems at room temperature (~22 °C).
Table 2
List of several commonly used fluorescence lifetime standard fluorophores
Fluorophore | Absorption peak a | Emission peaka | Solvent | Lifetimeb | Reference |
|---|---|---|---|---|---|
Coumarin 6 | ~460 nm | ~505 nm | Ethanol | ~2.5 ns | [46] |
HPTS | ~454 nm | ~511 nm | Phosphate buffer (pH 7.5) | ~5.3 ns | [46] |
Fluorescein | ~494 nm | ~521 nm | Phosphate or Tris buffer (pH > 7) | 4–4.1 ns | |
Rhodamine B | ~542 nm | ~565 nm | Water | ~1.7 ns | [54] |
Methanol | ~2.5 ns | [72] | |||
Ethanol | ~3.1 ns | ||||
Rose Bengal | ~560 nm | ~571 nm | Water | ~0.12 ns | |
Methanol | ~0.54 ns | ||||
Ethanol | ~0.74 ns | ||||
2-propanol | ~0.98 ns | ||||
Acetonitrile | ~2.38 ns | ||||
Acetone | ~2.57 ns |
1.
Coumarin 6 dissolved in ethanol (~2.5 ns).
2.
Fluorescein dissolved in Tris buffer at pH 7.5 (~4.05 ns).
3.
Rose Bengal dissolved in water (~0.12 ns).
4.
Rose Bengal dissolved in methanol (~0.54 ns).
5.
Rose Bengal dissolved in 2-proponal (~0.98 ns).
6.
Rose Bengal dissolved in methanol (~2.57 ns).
2.5 FRET Standards for Verification of a FLIM-FRET Approach
It is desirable to employ FRET reference standards in addition to positive and negative controls to verify the FLIM-FRET results. A comparative method to determine the accuracy of FRET measurements was developed by the Vogel laboratory (NIH/NIAAA) [74, 75]. The approach uses “standards” in the form of genetic constructs encoding fusions between donor and acceptor fluorescent proteins separated by defined amino acid (aa) linker sequences. A series of FRET-standard constructs were generated through encoding Cerulean [76] and Venus [77], directly coupled by either a 5, 17, or 32 aa linker—named as C5V, C17V, and C32V, correspondingly [75]. In addition, a construct of a low FRET efficiency as a negative control was also made using a 229 aa linker and is named CTV, where Cerulean and Venus are separated by a TRAF domain [74]. These plasmids are now available at www.addgene.org/Steven_Vogel. Here, three FRET-standard constructs expressed in live mouse pituitary GHFT1 cells (transfected by FuGENE 6) are used to verify both TCSPC and FD FLIM-FRET approaches.
1.




Cells alone without any transfection.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


