(8.1)
In the end, the analyst will obtain, for each individual j, a value for: (a) the intercept π 0 , which defines the predicted value of Y when age = 0; (b) the slope π 1 , which defines the predicted change (either positive for growth or negative for decline) of Y for each unit change (e.g., one year, one month) in age; (c) the standard error of the estimate, which is closely related to the variability of the errors E i at each time point and which defines the quality of the overall age prediction of Y. Note that to interpret the intercept, it is customary to center age around a meaningful value, such as the average of the sample (by subtracting from each individual’s age the sample average age). The intercept is then the predicted Y value for an individual of average age. Alternative age scalings have been proposed and might allow for a more meaningful interpretation of the intercept in particular research situations (e.g., Mehta and West 2000; Wainer 2000). The assumptions of the model are that the errors E i are normally distributed (i.e., they follow a normal, Gaussian curve) and do not depend on values of age (i.e., homoscedasticity).
If the model is estimated for each individual, n estimates of these parameters are obtained. Of course, other mathematical relations between age and Y can be tested, such as polynomial or exponential functions (for instance, to model human growth, various exponential functions have been proposed). What must be kept in mind is that so far the analysis is individual-specific. At the first analytical step, the growth model is estimated for each individual. At the second analytical step, the individual estimates are subsequently summarized. Any conclusion about the overall sample would have to be inferred by summarizing the n estimates, for instance by calculating the average and the variance of the intercepts and of the slopes across all individuals. Note that the two steps are computed independently of each other.
The Linear Mixed-Effects Model
In 1982 Laird and Ware proposed a model that allowed estimating simultaneously intercept and slope information at both the individual and the sample level. The model is an expansion of the individual growth model and is presented in Eq. 8.2.
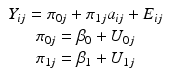
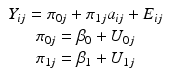
(8.2)
Given that the repeated assessments of Y of all individuals are analyzed simultaneously, Eq. 8.2 necessitates the addition of the subscript j, which identifies the individual. Moreover, this approach supposes one set of growth parameters, that is, one intercept and one slope, per individual, which again justifies the subscript j on both parameters π 0 and π 1 . Technically, it is not correct to say that an intercept and a slope value are estimated for each individual. That is, the model does not explicitly estimate a π 0j and a π 1j value for each individual j. The model presupposes, however, that each individual may have an intercept and a slope value that deviate from the central (population average) values, which are indicated by β 0 and β 1 and which are explicitly estimated. What are also estimated are the inter-individual variances, due to the individual deviations U 0j and U 1j around the central values, and possibly the covariance between U 0j and U 1j . The variances of the U 0j and U 1j are defined by the parameters σ 2 I and σ 2 S , respectively, and their covariance by the parameter σ IS . Lastly, the errors of prediction E ij are not individually estimated. These are often assumed to have a constant variance in time, estimated by the parameter σ 2 E , and to be uncorrelated in time. In sum, then, in its most frequent specification, this model estimates six parameters: two central values, for the intercept, β 0 , and the slope, β 1 , two variances and a covariance of growth parameters, σ 2 I , σ 2 S , and σ IS , and an error variance σ 2 E . Figure 8.1 illustrates schematically the parameters of the linear mixed-effects model (LMEM).
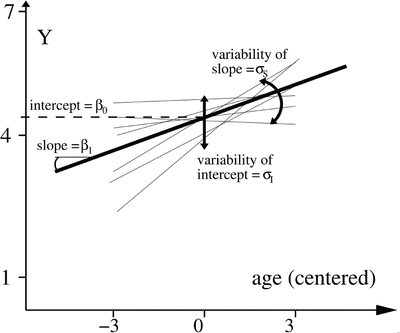

Fig. 8.1
Schematic representation of the parameters estimated in the LMEM (Eq. 8.2). The thin lines represent the best-fitting trajectory of each individual, while the thick line represents the best-fitting trajectory based on the central values (representative of the overall sample). In this example the value of the slope, β 1 , is positive. Note that the estimated slope variance, σ 2 S , and intercept-slope covariance, σ IS , depend on where age has been centered
This model distinguishes two kinds of parameters: the central values, which are common to all individuals (β 0 and β 1 ) and are called fixed effects, and the individual deviations from these central values (U 0j and U 1j ), called the random effects. Again, the random effects and the individual errors (E ij ) are not directly estimated, but their variances and covariance (σ 2 I , σ 2 S , σ IS , and σ 2 E ) are. Fixed effects thus apply to all individuals and are not subject to individual variations. Random effects, on the other hand, vary across individuals and do so by typically following the standard distribution of random variables, that is, a normal (Gaussian) distribution. The model hence assumes that all random effects (U 0j , U 1j ) and errors (E ij ) are normally distributed (symbolized by U 0j ∼ 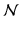 (0, σ 2 I ), U 1j ∼
(0, σ 2 I ), U 1j ∼ 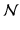 (0, σ 2 S ), and E ij ∼
(0, σ 2 S ), and E ij ∼ 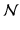 (0, σ 2 E )), that the random effects may covary (Cov(U 0j , U 1j ) = σ IS ), that the errors do not covary with the random effects (Cov(E ij , U 0j ) = Cov(E ij , U 1j ) = 0), and that the errors do not covary in time (Cov(E ij , E i’j ) = 0).
(0, σ 2 E )), that the random effects may covary (Cov(U 0j , U 1j ) = σ IS ), that the errors do not covary with the random effects (Cov(E ij , U 0j ) = Cov(E ij , U 1j ) = 0), and that the errors do not covary in time (Cov(E ij , E i’j ) = 0).
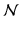 (0, σ 2 I ), U 1j ∼
(0, σ 2 I ), U 1j ∼ 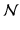 (0, σ 2 S ), and E ij ∼
(0, σ 2 S ), and E ij ∼  (0, σ 2 E )), that the random effects may covary (Cov(U 0j , U 1j ) = σ IS ), that the errors do not covary with the random effects (Cov(E ij , U 0j ) = Cov(E ij , U 1j ) = 0), and that the errors do not covary in time (Cov(E ij , E i’j ) = 0).
(0, σ 2 E )), that the random effects may covary (Cov(U 0j , U 1j ) = σ IS ), that the errors do not covary with the random effects (Cov(E ij , U 0j ) = Cov(E ij , U 1j ) = 0), and that the errors do not covary in time (Cov(E ij , E i’j ) = 0).The coexistence of fixed and random effects within the same model gives it the name of the linear mixed-effects model. The term linear denotes that the function linking Y to the predictor a ij is linear in its parameters, meaning that the parameters associated to the prediction of Y (on the right side of the equal sign in Eq. 8.2) are at most multiplied by a predictor and then added (i.e., the prediction is a linear combination of the parameters and the predictors), rather than, for instance, being exponentiated. This model has been developed in different disciplines, and is also known as random-effects model (Laird and Ware 1982), hierarchical linear model (Bryk and Raudenbush 1987), and multilevel model (Goldstein 1989).
The LMEM of Eq. 8.2 has notable advantages over the individually estimated growth models of Eq. 8.1. First, the estimation is simultaneous, that is, instead of involving two analytical steps it can be computed in a single step. All n individuals’ data are analyzed together, in a single analysis. This makes for a considerable gain in time. Second, the statistical tests obtained with the LMEM are superior to those of individually estimated growth models. More precisely, the Type I error rate of statistical tests is closer to its nominal value within the LMEM than in individual growth models, which are usually too liberal (Snijders and Bosker 2012). Third, the LMEM allows for a statistical test of sample heterogeneity, which is not possible with the individual growth approach. Hence, statistical tests for the significance of variances and covariance of the random effects (σ 2 I , σ 2 S , and σ IS ) are possible within the LMEM. This feature is extremely important, as these parameters represent heterogeneity in growth parameters, a concept often of chief interest from a theoretical perspective. Fourth, the LMEM can be extended to define parameters that operationalize the five objectives of longitudinal research: (a) Intraindividual change is directly identified with the first line of Eq. 8.2, and β 0 and β 1 define the average intraindividual change function; (b) the intercept variance σ 2 I and the slope variance σ 2 S identify directly interindividual differences in intraindividual change; (c) in multivariate specifications of the LMEM it is possible to covary intercept and slope of one change process with those of another (MacCallum et al. 1997; more detail in the section “Three Notable Extensions”, below); (d) it is straightforward to add a predictor to the first line of Eq. 8.2 to test a determinant of intraindividual change; and (e) if intercept variance and slope variance are significant, it is straightforward to extend the LMEM to include a predictor of interindividual differences in intraindividual change (more detail in the section “Inclusion of Covariates”, below). In other words, the LMEM appears to provide explicit statistical tests directly associated to the rationale and objectives of longitudinal research enunciated by Baltes and Nesselroade (1979). Consequently, this statistical model addresses key theoretical questions of life course research.
The Latent Curve Model
In 1984, Meredith and Tisak 1984 presented the precepts of how the LMEM defined above can be specified as a structural equation model. The work was later formalized by the same authors (Meredith and Tisak 1990), and applied by McArdle (1986). Structural equation modeling can largely be defined as a set of statistical techniques aimed at testing hypothesized relationships among chosen variables. In this context, the Latent Curve Model (LCM) formalizes how a series of repeated measurements of variable Y for individual j, represented by the vector Y j, is related to the passing of time (or aging of the individual) as specified in Eq. 8.3 (note that it is customary to write the names of vectors and matrices in boldface).
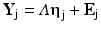
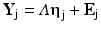
(8.3)
For each individual j, the T repeated measurements of Y are piled up in the vector Y j (of size T × 1, corresponding to Y 1j to Y Tj in Eq. 8.2). η j represents the vector (of size 2 × 1) of the two growth factors (or latent variables), intercept and slope (equivalent to π 0j and π 1j in Eq. 8.2). Λ is the matrix (of size T × 2) of the factor loadings associating the repeated observations to the growth factors. Note that Λ is not indexed by j, indicating that its values are the same for all individuals. Finally, E j is the vector (of size T × 1, corresponding to E 1j up to E Tj in Eq. 8.2) of time-specific errors. The loadings associating the intercept to the measurements (i.e., the first column of Λ) are conveniently fixed at 1 (the multiplier of π 0j in Eq. 8.2). To specify linear change, the loadings of the slope factor (i.e., the second column of Λ) increase linearly with time, or age. Hence, in this basic specification, the elements of the loading matrix Λ are not estimated. For instance, if the sample is observed at five ages, the loadings of the intercept would be [1 1 1 1 1]’ while for the slope they might be [−2 −1 0 1 2]’, (the values of a ij in Eq. 8.2; the prime symbol ’ stands for transposed). This is equivalent to centering the variable age on the third value in the LMEM. To clarify, we expand the general LCM notation in an illustration below (cf. Eq. 8.7).
The crucial parameter estimates of the LCM are associated to the growth factors η. The central values of the intercept and of the slope factor correspond to the fixed effects β 0 and β 1 of the LMEM; the variances of the two factors correspond to σ 2 I and σ 2 S and their covariance corresponds to σ IS . Finally, if the error variance is constrained to be constant in time, its estimate corresponds to σ 2 E . In the end, it can be shown that, while they have originated in rather widely different fields of statistics, the LMEM and the LCM as specified here are completely equivalent (e.g., Bauer 2003; Chou et al. 1998; McArdle and Hamagami 1996).
Inclusion of Covariates
The growth model implemented via the LMEM or the LCM allows for testing sample heterogeneity in the growth factors. For instance, are individuals different from each other with respect to their intercept score? This question is operationalized by testing the null hypothesis that the intercept variance is zero (H0: σ 2 I = 0). Likewise, we can ask whether there are individual differences in the change process, or whether the entities are different from each other with respect to their slope score. Testing the null hypothesis of zero slope variance (H0: σ 2 S = 0) addresses this question. If there appear to be interindividual differences in intercept and in slope (i.e., if the two variances are different from zero), a natural question is whether the intercept and the slope scores are related. This question is addressed by the null hypothesis of zero covariance (H0: σ IS = 0).
If sample heterogeneity in intercept and/or slope appears significant, we can wonder whether a given characteristic of the entity may influence the growth factors. This question can easily be addressed within the LMEM and LCM by expanding the models to include predictors. There are two kinds of predictors. Time-varying predictors are those that vary across time, such as a medical or physical measurement taken at each assessment time, and hence require not only a subscript j to determine the individual, but also a subscript i to specify their time of assessment. These predictors are also called time-dependent or level 1 and may help explain intraindividual change. Time-invariant predictors, on the other hand, are individual specific and do not change in time, such as sex. These are simply denoted with a subscript j and are also called level 2, and may help explain interindividual differences in intraindividual change.
The LMEM can be expanded to include a time-varying predictor x ij and a time-invariant predictor z j as shown in Eq. 8.4.
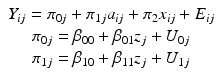
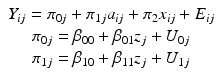
(8.4)
In the LCM the inclusion of a time-varying and a time-invariant predictor is shown in Eq. 8.5 (in which we use the notation that is standard in the structural equation modeling literature; e.g., Bollen and Curran 2006).
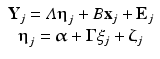
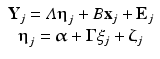
(8.5)
Equation 8.5 specifies that the outcome Y j is not only influenced by the growth factors η j, but also by an observed time-varying covariate x j, through a regression weight specified in the scalar B (equivalent to π 2 in Eq. 8.4). The vector x j has T rows and one column, while the scalar B is a single number. The growth factors η j may be influenced by a time-invariant covariate ξ j (z j in Eq. 8.4) via the regression intercepts α (β 00 and β 10 in Eq. 8.4) and the regression weights Γ (β 01 and β 11 in Eq. 8.4). Given that the prediction of η j by ξ j will likely not be perfect in practice, Eq. 8.5 includes the regression errors ζ j (U 0j and U 1j in Eq. 8.4). Again, it can be shown that the models in Eqs. 8.4 and 8.5 are equivalent.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


