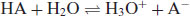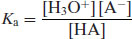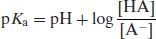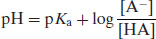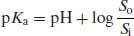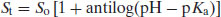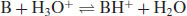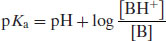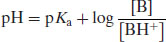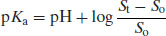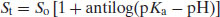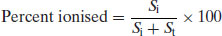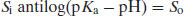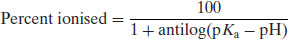Understanding acid and base behaviour is extremely important, not only because of the sheer number of ionisable drug substances but because the solubility of an acidic or basic drug substance will be pH-dependent. Possession of an ionisable functional group also opens the possibility of solubility manipulation via salt formation, so long as the salt is stable at physiological pH.
2.2 Ionisation
Understanding the character of weak acids and bases starts with consideration of the partial ionisation that will occur following dissolution in water. Using the notation HA to represent an acid
where H3O+ is the hydronium ion (the H+ ion does not exist in isolation in water). Strong acids will dissociate almost completely, shifting the position of equilibrium of Equation (2.1) virtually to the right-hand side, but weak acids will only partially ionise. The equilibrium constant (or ionisation constant in this instance) can be represented by
Note that water is considered to be present in excess and so does not appear in Equation (2.2). Taking logarithms of both sides yields
(2.3)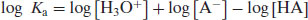
Reversing the signs gives
(2.4)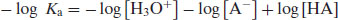
Using the notation p to represent negative logarithm (and noting that –log [H3O+] is represented by pH) gives
(2.5)
and so
or
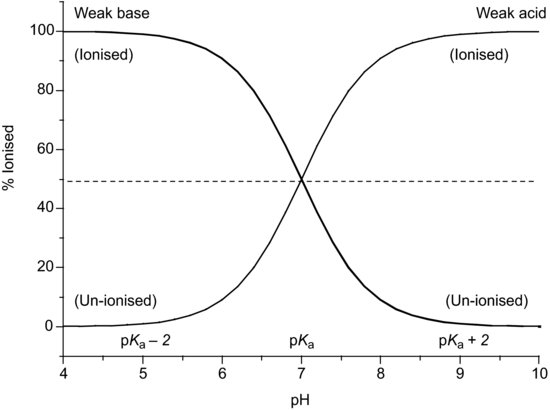
Equations (2.6) and (2.7) are known as the Henderson–Hasselbalch equations and allow calculation of the extent of ionisation of an acidic drug substance as a function of pH if the pKa is known. When the pH is significantly below the pKa (by at least 3 pH units) a weakly acidic drug substance will be completely un-ionised and when the pH is significantly above the pKa (by at least 3 pH units) a weakly acidic drug substance will be fully ionised (Figure 2.1).
The degree of ionisation will affect the measured solubility because ionised drug substances are generally more soluble in water. Since [A−] represents the saturated concentration of the ionised drug substance (Si) and [HA] represents the saturated concentration of the un-ionised drug substance (i.e. the intrinsic solubility, So), then
At any given pH the observed total solubility (St) must be the sum of the un-ionised and ionised fractions:
(2.9)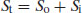
Rearranging gives
(2.10)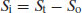
Substituting in Equation (2.8) gives
(2.11)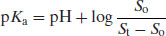
or, in antilog form,
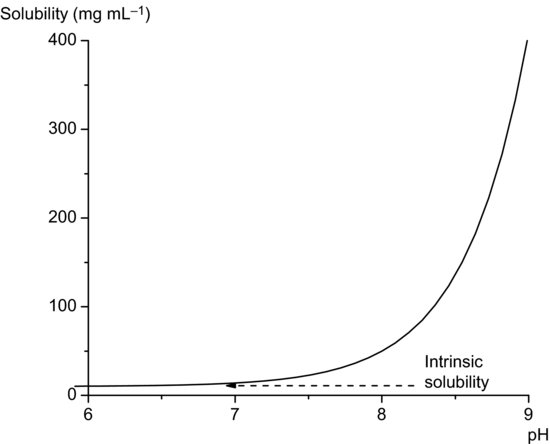
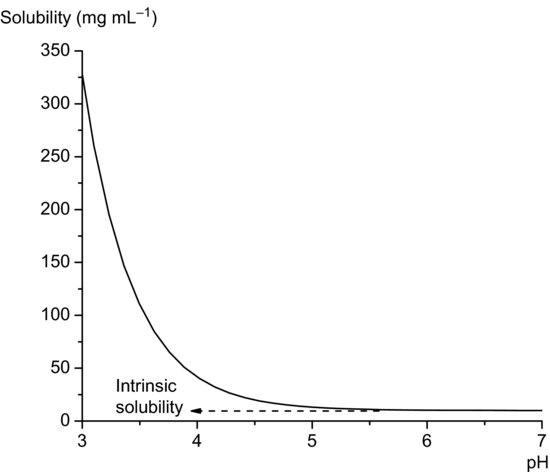
Equation (2.12) allows calculation of the total solubility of an acidic drug substance as a function of pH. Total solubility will be equal to the intrinsic solubility at pH values at least 3 below pKa and will increase significantly at pH values above pKa (Figure 2.2). In theory, Equation (2.12) predicts an infinite increase in solubility when pH >> pKa. In practice this is not attained, real systems deviating from ideal behaviour because of solute–solvent interactions and because salt forms will also have a limiting solubility, but Equation (2.12) is nevertheless a useful approximation over narrow pH ranges.
Example 2.1 The pKa of the weakly acidic drug substance sulphapyridine is 8.0. What is the ratio of un-ionised to ionised sulphapyridine in blood plasma (pH 7.4)?
From Equation (2.8),
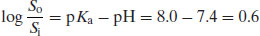
So the ratio of un-ionised to ionised drug must be
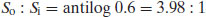
A similar derivation can be made for weak bases. Starting with the notation B to represent the base,
Traditionally a base ionisation constant would be written (Kb) but this has been superseded (somewhat confusingly1) by the universal use of acid ionisation constants (i.e. considering the process in Equation (2.13) from right to left) and so
(2.14)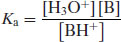
If the same logic is applied as above then it is possible to derive
or
As in the case of weak acids, the total solubility will be the sum of the solubilities of the ionised and un-ionised moieties and so again following the logic described earlier, the following equations can be described as
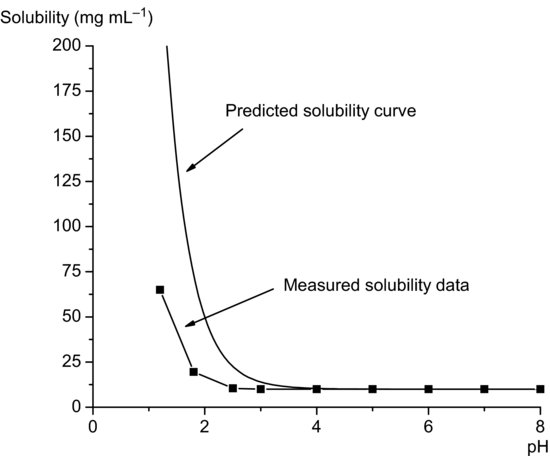
Equation (2.18) implies that total solubility will be equal to the intrinsic solubility at pH values at least 3 above pKa and will increase significantly at pH values below pKa (Figure 2.3). Note again that the solubility profile predicted from Equation (2.18) assumes ideal behavior and that in practice measured solubility often deviates from ideality. The data in Figure 2.4 for metronidazole (pKa 2.6) illustrate this point.
Figure 2.4 Solubility data for metronidazole, showing the difference between experimentally measured solubility data and the curve predicted using Equation (2.18) (solubility data from Wu and Fassihi (2005)).
Study question 2.1 Derive Equations (2.17) and (2.18).
Study question 2.2 Look at the solubility data for Lipitor (atorvastatin calcium) and Seroquel (quetiapine fumarate) in Table 2.1. Can you tell which drug is a weak acid and which is a weak base?
- If a drug substance has an ionisable group, then solubility will vary with pH.
- The ionisation constant is known as the pKa.
- Acidic drugs will be more soluble when pH >> pKa.
- Basic drugs will be more soluble when pH << pKa.
- When pH = pKa the drug is 50% ionised.
- The Henderson–Hasselbalch equations allow prediction of solubility as a function of pH.
2.2.1 Percent ionisation
Rearrangement of the Henderson–Hasselbalch equations allows calculation of the percentage of drug substance ionised as a function of pH. Starting with the premise that
Rearranging the Henderson–Hasselbalch equation for acid species (Equation (2.8)) yields
(2.20)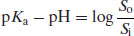
Taking antilogs gives
(2.21)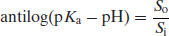
or
Substituting Equation (2.22) into Equation (2.19) yields
(2.23)
or, dividing through by Si,
Equation (2.24) (and the equivalent form for basic drug substances – see Study question 2.1) allows calculation of the percent ionised as a function of pH with respect to pKa. Some values are given in Table 2.2 for reference.
Table 2.2 Percent ionised for weak acids and bases as a function of pH.
| Percent ionised | ||
| pKa – pH | Weak acid | Weak base |
| –4 | 99.99 | 0.01 |
| –3 | 99.94 | 0.06 |
| –2 | 99.01 | 0.99 |
| –1 | 90.91 | 9.09 |
| –0.9 | 88.81 | 11.19 |
| –0.8 | 86.30 | 13.70 |
| –0.7 | 83.37 | 16.63 |
| –0.6 | 79.93 | 20.07 |
| –0.5 | 75.97 | 24.03 |
| –0.4 | 71.53 | 28.47 |
| –0.3 | 66.61 | 33.39 |
| –0.2 | 61.32 | 38.68 |
| –0.1 | 55.73 | 44.27 |
| 0 | 50 | 50 |
| 0.1 | 44.27 | 55.73 |
| 0.2 | 38.68 | 61.32 |
| 0.3 | 33.39 | 66.61 |
| 0.4 | 28.47 | 71.53 |
| 0.5 | 24.03 | 75.97 |
| 0.6 | 20.07 | 79.93 |
| 0.7 | 16.63 | 83.37 |
| 0.8 | 13.70 | 86.30 |
| 0.9 | 11.19 | 88.81 |
| 1 | 9.09 | 90.91 |
| 2 | 0.99 | 99.01 |
| 3 | 0.06 | 99.94 |
| 4 | 0.01 | 99.99 |
Study question 2.3 Derive an equation that allows determination of percent ionisation as a function of pH for basic drug substances.
2.3 Buffers
Clearly, when an acid is added to an aqueous solution the pH will drop and when a base is added to an aqueous solution the pH will rise (this phenomenon is used as the basis of a therapeutic treatment – antacids). Sometimes, it is preferable to have a solution that resists changes in pH upon dissolution of a solute (because solubility, percent ionisation and some reaction rates are pH-dependent). A solution designed to resist changes in pH upon addition of an acid or base is known as a buffer. A buffer system usually comprises a weak acid or base and its corresponding salt. An example would be a combination of acetic acid and sodium acetate:
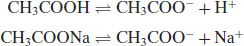
Acetic acid is a weak acid and therefore its position of equilibrium lies to the left. Sodium acetate is a salt and will dissociate fully, so its equilibrium lies to the right. If H+ ions are added they will react with CH3COO− ions to give acetic acid. This is a weak acid and so only ionises slightly. The pH thus remains practically constant. Similarly, if OH− ions are added they react with acetic acid to give water and acetate ions. Again, the pH only changes slightly. Buffers usually work best when the pH being maintained is equal or near to the pKa of the weak acid or base used. Buffer capacity (the number of moles of acid or base that must be added to a buffer system to produce a decrease or increase of 1 pH unit) can be determined from the Henderson–Hasselbalch equation:
(2.25)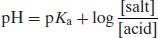
2.4 Determination of pKa
There are numerous methods to measure pKa. Prankerd (2007) provides an excellent introduction to the methods available as well as comprehensive tables of pKa data for existing drugs and notes the most accurate methods are those based on conductance (reliable to ±0.0001 pK unit or better) or electrochemical cells without liquid junction potentials (reliable to ±0.001 pK unit or better). Pharmaceutical pKa values are usually determined with methods based on a relationship between solution pH and a physicochemical property, such as added titrant concentration, spectrophotometric absorb- ance, optical rotation or fluorescence intensity. Prankerd (2007) notes that using any approach based on measurement of pH immediately limits the accuracy and precision of the result to no better than ±0.02 pK unit.
IUPAC has published descriptive terms for the error of pKa measurements (Table 2.3). Although the errors appear small, it must be remembered that pKa expresses the ionisation constant in logarithmic terms (the corresponding uncertainties in Ka are also shown in Table 2.3). Determination of pKa values with a method based on measurement of pH can therefore only result in a value that can be considered approximate at best and most likely uncertain. As noted earlier, during preformulation screening it is acceptable to determine approximate values since the data are used primarily to identify those drug substances with the best potential for development. Hence, initial pKa values should be regarded as uncertain.
Table 2.3 IUPAC descriptions for error in pKa values.
| Description | Error in pKa | Uncertainty in pKa |
| Very reliable | < ±0.005 | <1% |
| Reliable | ±0.005 to ±0.02 | ∼1% |
| Approximate | ±0.02 to ±0.04 | ∼5% |
| Uncertain | > ±0.04 | >10% |
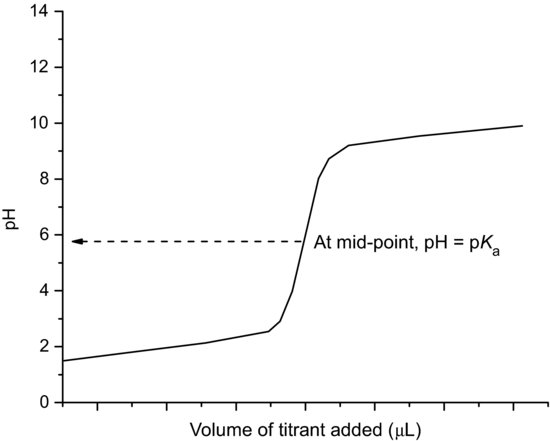
2.4.1 Determination of pKa by potentiometric titration
Modern automated instrumentation is available that can determine pKa values, by potentiometric titration, with very small (<10 mg) amounts of drug substance. The drug substance is dissolved in water, forming either a weakly acidic or weakly basic solution. Acid or base (as appropriate) solution is titrated and the solution pH recorded. A plot of volume of titrant solution added versus pH allows graphical determination of the pKa, since when pH = pKa the compound is 50% ionised (Figure 2.5). The method has the significant advantage of not requiring an assay for the analyte.
< div class='tao-gold-member'>